文章目录

前期知识
例题
- 337. 打家劫舍 III
相关练习题目
- 没有上司的舞会 https://www.luogu.com.cn/problem/P1352
- 1377. T 秒后青蛙的位置 https://leetcode.cn/problems/frog-position-after-t-seconds/⭐⭐⭐
- - 解法1：BFS
  - - 优化代码
  - 解法2——自顶向下dfs
  - 解法3——自底向上dfs
- 2646. 最小化旅行的价格总和 https://leetcode.cn/problems/minimize-the-total-price-of-the-trips/solution/lei-si-da-jia-jie-she-iii-pythonjavacgo-4k3wq/⭐⭐⭐⭐⭐
- - 解法1——暴力dfs每条路径
  - 解法2——Tarjan 离线 LCA + 树上差分
- 补充题目：2467. 树上最大得分和路径⭐⭐⭐

前期知识

最大独立集 需要从图中选择尽量多的点，使得这些点互不相邻。

在这里插入图片描述

例题

337. 打家劫舍 III

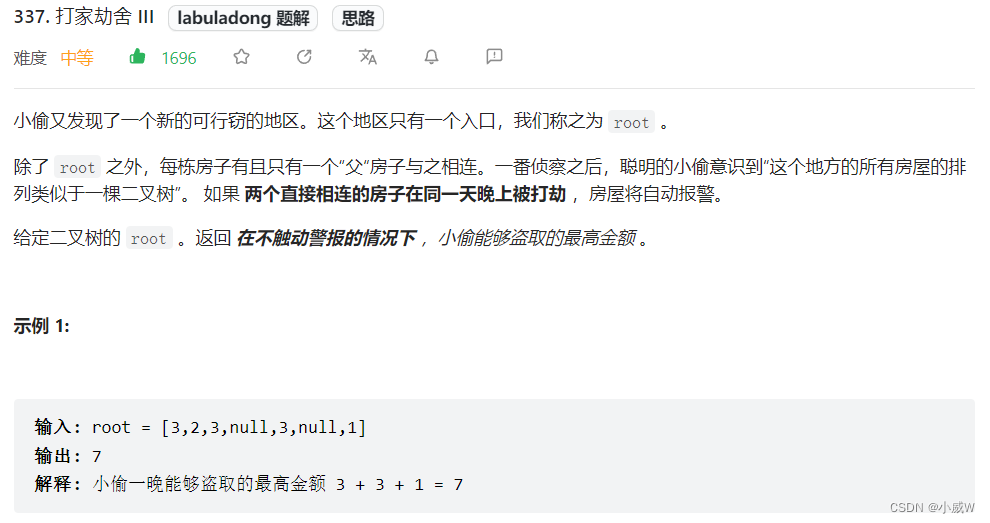
在这里插入图片描述
用一个数组 int[] = {a, b} 来接收每个节点返回的结果。返回值{a,b} a表示没选当前节点的最大值,b表示选了当前节点的最大值。

使用后序遍历dfs。（发现树形 DP 基本都是后序 dfs）

在这里插入图片描述

class Solution {
    public int rob(TreeNode root) {
        int[] res = dfs(root);
        return Math.max(res[0], res[1]);
    }

    public int[] dfs(TreeNode root) {
        // 返回值{a,b} a表示没选当前节点的最大值,b表示选了当前节点的最大值
        if (root == null) return new int[]{0, 0};
        int[] l = dfs(root.left), r = dfs(root.right);
        int a = Math.max(l[0], l[1]) + Math.max(r[0], r[1]), b = root.val + l[0] + r[0];
        return new int[]{a, b};
    }
}

相关练习题目

没有上司的舞会 https://www.luogu.com.cn/problem/P1352

P1352 没有上司的舞会

在这里插入图片描述
这道题目相当于每个节点可能会有若干个子节点的 337. 打家劫舍 III 。

因为是 ACM 模式，所以代码处理输入很冗长。

AC代码如下：

import java.util.*;

public class Main {
    static List<Integer>[] childs;	// 记录每个节点的子节点列表
    static int[] r;					// 记录每个节点的快乐指数

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        r = new int[n + 1];
        for (int i = 1; i <= n; ++i) r[i] = scanner.nextInt();
        childs = new ArrayList[n + 1];
        Arrays.setAll(childs, e -> new ArrayList());
        Set<Integer> s = new HashSet<>();	// 记录哪些节点没有父节点，把他们统一放在0节点之下
        for (int i = 1; i <= n; ++i) s.add(i);
        for (int i = 2; i <= n; ++i) {
            int l = scanner.nextInt(), k = scanner.nextInt();
            childs[k].add(l);
            s.remove(l);
        }
        for (int v: s) childs[0].add(v);    // 所有没有父节点的节点放在0节点之下
        int[] res = dfs(0);
        System.out.println(Math.max(res[0], res[1]));
        return;
    }

    public static int[] dfs(int rootId) {
        int a = 0, b = r[rootId];		// a表示不选当前节点，b表示选当前节点
        for (int i: childs[rootId]) {   // 枚举所有子节点
            int[] res = dfs(i);
            a += Math.max(res[0], res[1]);	// 不选当前节点，所以子节点选不选都可以
            b += res[0];					// 选当前节点，所以子节点只能不选
        }
        return new int[]{a, b};
    }
}

从代码模板来看，这里使用 for 循环来枚举当前节点的所有子节点。

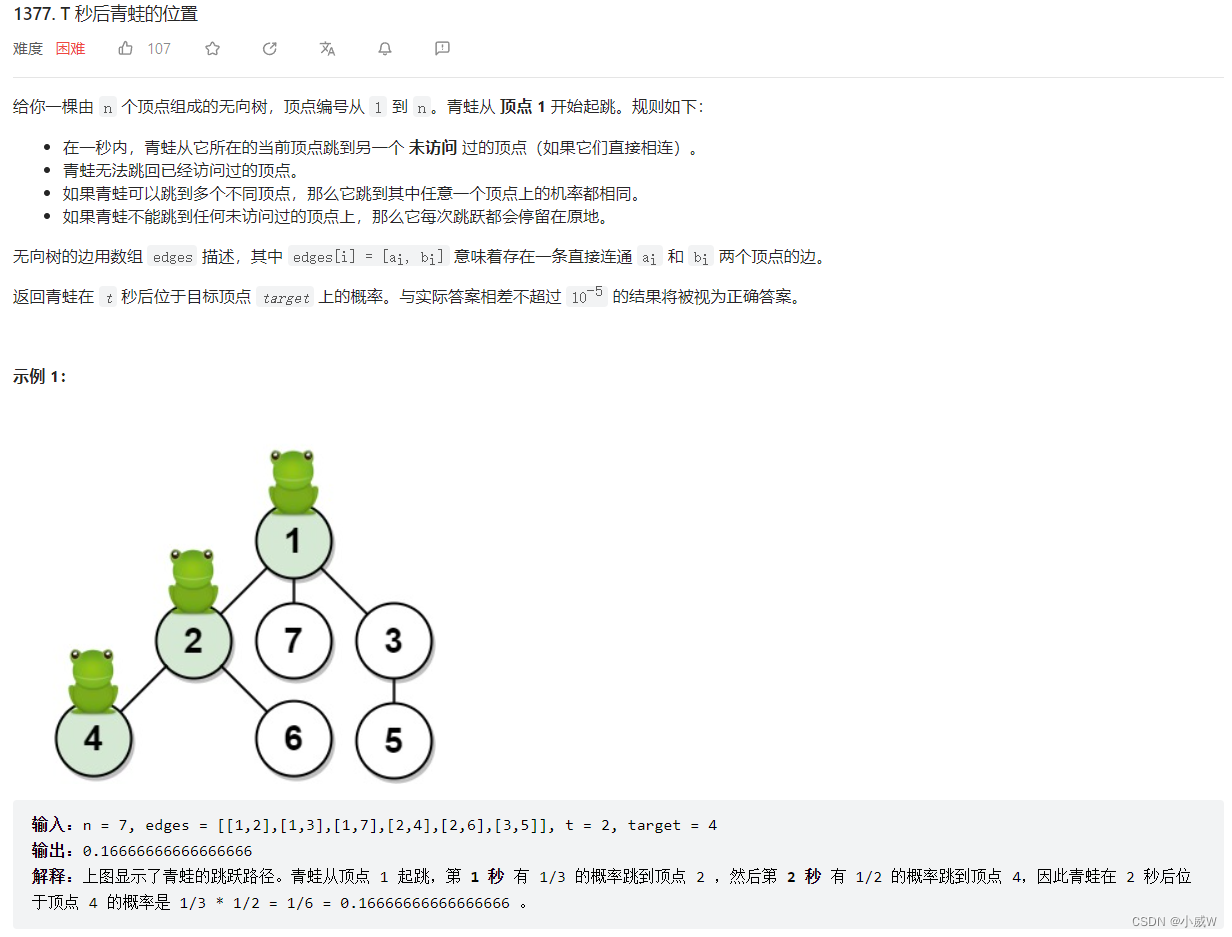
1377. T 秒后青蛙的位置 https://leetcode.cn/problems/frog-position-after-t-seconds/⭐⭐⭐

1377. T 秒后青蛙的位置

在这里插入图片描述

解法1：BFS

从题意来看，每次青蛙都会往下走一层，很像层序遍历，所以可以是用 bfs 来模拟整个过程。

在 bfs 的过程中，如果当前节点的概率为 p，他有 k 个子节点，那么它的所有子节点的概率就是 p / k，即在分母上乘了 k。
在这个过程中，我们可以记录各个节点的概率分母。

如果当前节点没有子节点，那么它的概率不变，再重新加入队列中。

class Solution {
    public double frogPosition(int n, int[][] edges, int t, int target) {
        // 建树
        List<Integer>[] g = new ArrayList[n + 1];
        Arrays.setAll(g, e -> new ArrayList());
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            g[x].add(y);
            g[y].add(x);
        }
        boolean[] st = new boolean[n + 1];
        // 由于某些样例在计算概率分母时会溢出int，因此使用long
        Queue<long[]> q = new LinkedList();
        q.offer(new long[]{1, 1});   // 将第一个节点放入队列
        st[1] = true;
        for (int i = 0; i <= t; ++i) {
            int sz = q.size();
            for (int j = 0; j < sz; ++j) {
                long[] cur = q.poll();
                // 如果达到了目标位置且时间正确，返回答案
                if (cur[0] == target && i == t) return 1.0 / cur[1];
                List<Integer> children = g[(int)cur[0]];
                boolean f = false;          // 记录它是否有子节点
                int cnt = 0;                // 记录它有几个子节点
                for (int child: children) {
                    if (!st[child]) ++cnt;
                }
                for (int child: children) {
                    if (!st[child]) {
                        q.offer(new long[]{child, cur[1] * cnt});    // 将子节点加入队列，概率的分母更新为cnt[1]*cnt
                        st[child] = true;
                        f = true;           // 说明有子节点
                    }
                }
                // 如果当前节点没有子节点，那么它还会待在当前位置
                if (!f) q.offer(cur);
            }
        }
        return 0;
    }
}

优化代码

优化的点包括：

修改了 return 结果的判断条件
删去了 cnt 统计每个节点的子节点个数，因为子节点数目就是g[x].size() - 1
给起始节点1增加一个父节点0，可以避免写多余判断

class Solution {
    public double frogPosition(int n, int[][] edges, int t, int target) {
        // 建树
        List<Integer>[] g = new ArrayList[n + 1];
        Arrays.setAll(g, e -> new ArrayList());
        g[1].add(0);		// 小技巧
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            g[x].add(y);
            g[y].add(x);
        }
        boolean[] st = new boolean[n + 1];
        // 由于某些样例在计算概率分母时会溢出int，因此使用long
        Queue<long[]> q = new LinkedList();
        q.offer(new long[]{1, 1});   // 将第一个节点放入队列
        st[1] = true;
        for (int i = 0; i <= t; ++i) {
            int sz = q.size();
            for (int j = 0; j < sz; ++j) {
                long[] cur = q.poll();
                // 如果达到了目标位置且时间正确，返回答案
                if (cur[0] == target) {
                    if (i == t || g[(int)cur[0]].size() == 1) return 1.0 / cur[1];
                    return 0;
                }
                List<Integer> children = g[(int)cur[0]];
                int cnt = children.size() - 1;                      // 记录它有几个子节点
                for (int child: children) {
                    if (!st[child]) {
                        q.offer(new long[]{child, cur[1] * cnt});    // 将子节点加入队列，概率的分母更新为cnt[1]*cnt
                        st[child] = true;
                    }
                }
            }
        }
        return 0;
    }
}

解法2——自顶向下dfs

整体思路与 bfs 类似。

class Solution {
    double ans;

    public double frogPosition(int n, int[][] edges, int t, int target) {
        // 建树
        List<Integer>[] g = new ArrayList[n + 1];
        Arrays.setAll(g, e -> new ArrayList());
        g[1].add(0);        	// 常用技巧：为了减少额外判断,给1加个父节点0
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            g[x].add(y);
            g[y].add(x);
        }
        dfs(g, target, 1, 0, t, 1);
        return ans;
    }

    public boolean dfs(List<Integer>[] g, int target, int x, int father, int leftTime, long prod) {
        // 如果x == target 且 （正好在t秒或处在叶子节点上）
        if (x == target && (leftTime == 0 || g[x].size() == 1)) {
            ans = 1.0 / prod;
            return true;
        }
        if (x == target || leftTime == 0) return false;
        for (int y: g[x]) {     // 遍历x的儿子y
            if (y != father && dfs(g, target, y, x, leftTime - 1, prod * (g[x].size() - 1))) {
                return true;    // 找到了就不再递归了
            }
        }
        return false;
    }
}

这里学到的重要技巧：

每个节点只会有一个父节点，因此它的子节点数量就是 g[x].size() - 1，不需要单独计算了。
g[1].add(0); // 常用技巧：为了减少额外判断,给1加个父节点0
dfs 返回 boolean 值，在 if () 中进行 dfs。

解法3——自底向上dfs

class Solution {
    double ans;

    public double frogPosition(int n, int[][] edges, int t, int target) {
        // 建树
        List<Integer>[] g = new ArrayList[n + 1];
        Arrays.setAll(g, e -> new ArrayList());
        g[1].add(0);        // 为了减少额外判断,给1加个父节点0
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            g[x].add(y);
            g[y].add(x);
        }
        long prod = dfs(g, target, 1, 0, t);
        return prod == 0? prod: 1.0 / prod;
    }

    public long dfs(List<Integer>[] g, int target, int x, int father, int leftTime) {
        // 找到结果的两种情况
        if (leftTime == 0) return x == target? 1: 0;
        if (x == target) return g[x].size() == 1? 1: 0;
        // 遍历 x 的儿子 y
        for (int y: g[x]) {
            if (y != father) {
                long prod = dfs(g, target, y, x, leftTime - 1);
                if (prod != 0) return prod * (g[x].size() - 1);
            }
        }
        return 0;
    }
}

自底向上的优点在于，只有找到了 target 之后才会做乘法计算 prod。

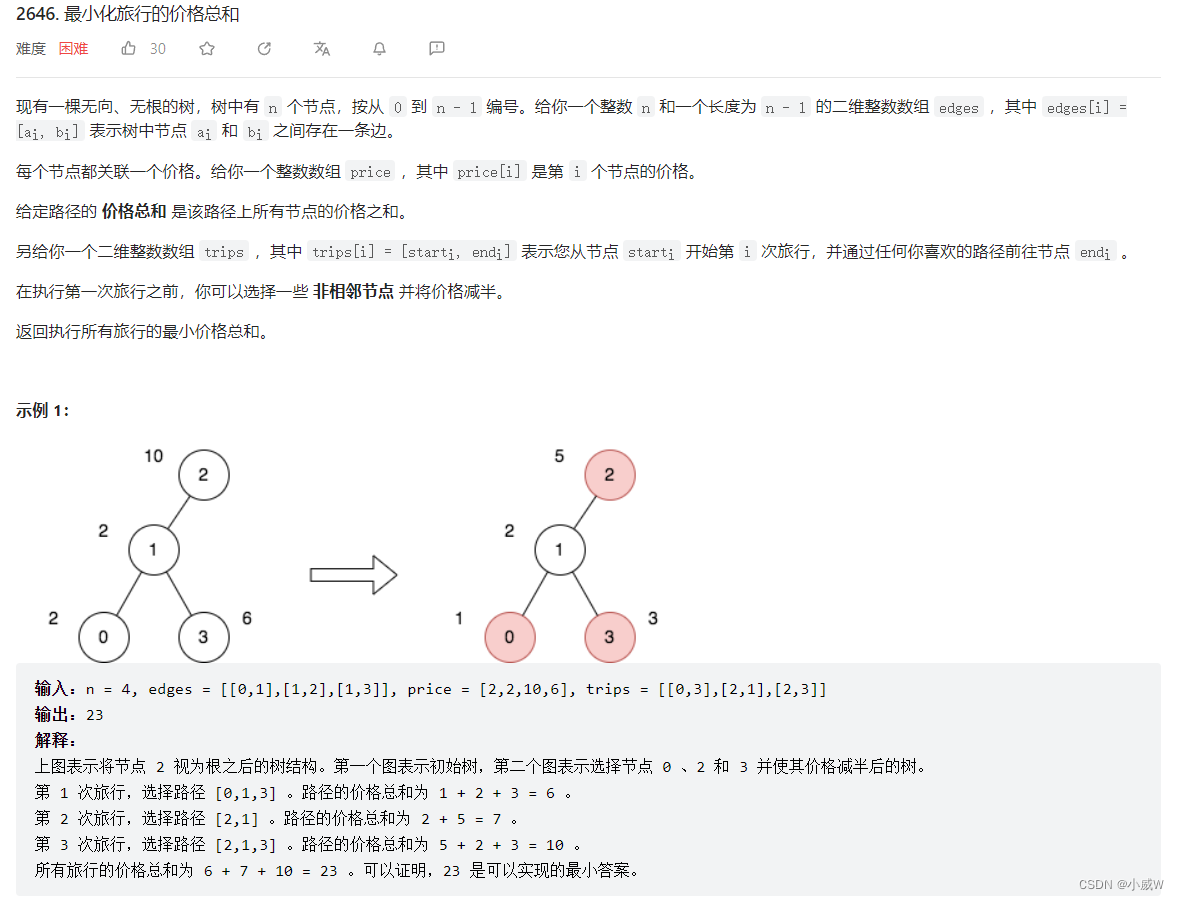
2646. 最小化旅行的价格总和 https://leetcode.cn/problems/minimize-the-total-price-of-the-trips/solution/lei-si-da-jia-jie-she-iii-pythonjavacgo-4k3wq/⭐⭐⭐⭐⭐

2646. 最小化旅行的价格总和

在这里插入图片描述

解法1——暴力dfs每条路径

在这里插入图片描述

核心思路是遍历每条路径，修改 price 数组，然后将问题转换成 337. 打家劫舍 III 。

class Solution {
    List<Integer>[] g;
    int[] price, cnt;
    int end;

    public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList());
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            g[x].add(y);
            g[y].add(x);
        }
        this.price = price;
        cnt = new int[n];       // 记录每个节点在路径中出现的次数
        for (int[] trip: trips) {
            end = trip[1];
            op(trip[0], -1);    // 用dfs找到这个trip路径上的点   
        }

        int[] p = dfs(0, -1);
        return Math.min(p[0], p[1]);
    }

    public boolean op(int x, int father) {
        if (x == end) {     // 找到了end
            ++cnt[x];
            return true;
        }
        for (int y: g[x]) {
            if (y != father && op(y, x)) {
                ++cnt[x];
                return true;
            }
        }
        return false;       // 没找到
    }

    // 返回值 ：[不减半，减半]
    public int[] dfs(int x, int father) {
        int notHalve = price[x] * cnt[x], halve = notHalve / 2;
        for (int y: g[x]) {
            if (y != father) {
                int[] p = dfs(y, x);
                notHalve += Math.min(p[0], p[1]);   // 当前不减半，那前面的节点随意
                halve += p[0];      // 当前减半，那前面的节点只能不减半
            }
        }
        return new int[]{notHalve, halve};
    }
}

解法2——Tarjan 离线 LCA + 树上差分

TODO
https://leetcode.cn/problems/minimize-the-total-price-of-the-trips/solution/lei-si-da-jia-jie-she-iii-pythonjavacgo-4k3wq/

补充题目：2467. 树上最大得分和路径⭐⭐⭐

2467. 树上最大得分和路径

在这里插入图片描述
这道题目更多的是练习树的 dfs 技巧，与 dp 关系不大。

使用两个 dfs ，
第一个 dfs 用于计算 bob 达到各点的时间，为计算 alice 路径上的价值做准备。
第二个 dfs 用于枚举 alice 到达各个叶子节点的路径，在达到叶子节点时更新答案。

class Solution {
    List<Integer>[] g;
    int[] bobTime, amount;
    int ans = Integer.MIN_VALUE;

    public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
        int n = edges.length + 1;
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList());
        for (int[] edge: edges) {
            int x = edge[0], y =edge[1];
            g[x].add(y);
            g[y].add(x);
        }
        g[0].add(-1);   // 常用技巧，给0节点加一个父节点-1，可以少写多余判断

        this.amount = amount;
        bobTime = new int[n];           // 记录bob到达该节点的时间
        Arrays.fill(bobTime, Integer.MAX_VALUE);    // 初始化为bob都到不了
        dfsBob(bob, 0, -1);
        dfsAlice(0, 0, -1, 0);
        return ans;
    }

    // 当前节点、当前节点的时间、当前节点的父节点
    public boolean dfsBob(int x, int time, int father) {
        // 只有到达了目的地才设置时间
        if (x == 0) {
            bobTime[x] = time;
            return true;
        }
        for (int y: g[x]) {
            if (y != father && dfsBob(y, time + 1, x)) {
                bobTime[x] = time;
                return true;
            }
        }
        return false;
    }

    public void dfsAlice(int x, int time, int father, int score) {
        // 计算当前节点的值
        int curVal = 0;
        if (time == bobTime[x]) curVal = amount[x] / 2;
        else if (time < bobTime[x]) curVal = amount[x];     // a早到
        // 到达了叶子节点，使用该条路径的值更新答案
        if (g[x].size() == 1) {
            ans = Math.max(ans, score + curVal);
            return;
        }
        // dfs过程
        for (int y: g[x]) {
            if (y != father) {
                dfsAlice(y, time + 1, x, score + curVal);
            }
        }
        return;
    }
}