二叉搜索树-技术点

news2024/12/27 12:18:54

二叉树的描述

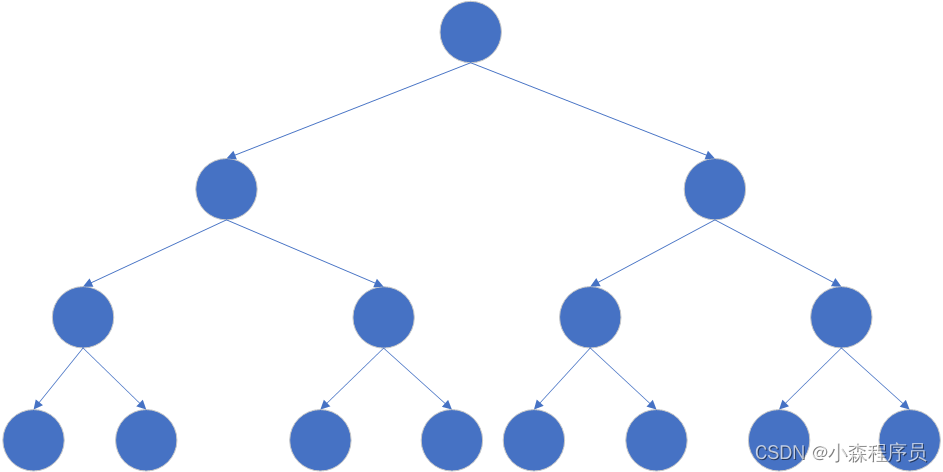
在这里插入图片描述

相当于给树来个计划生育

二叉树的原理

二叉树只允许最多两个节点 二叉树节点最多有两个节点 并不是一定要有两个分支节点
如图所示:
在这里插入图片描述

  • 在非空的二叉树里,具有i-1层的节点的总数不超过2的i-1次方 i>=1
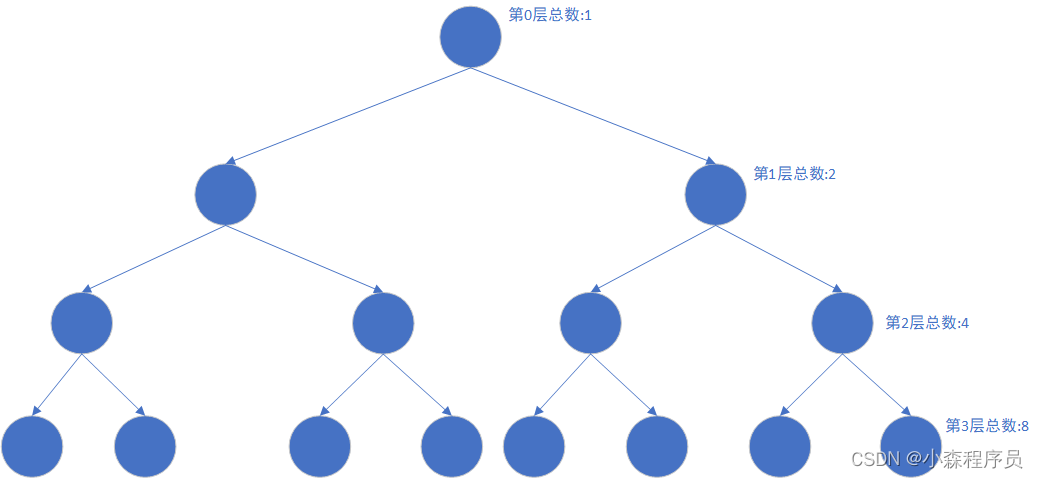
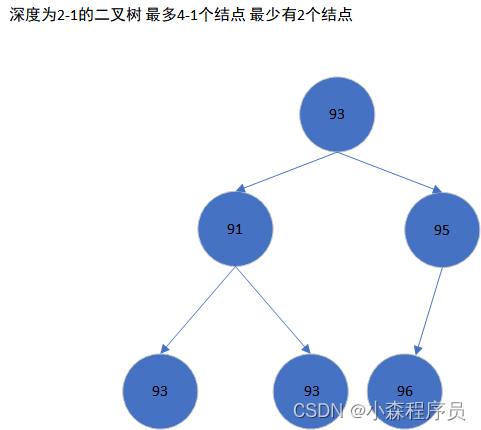
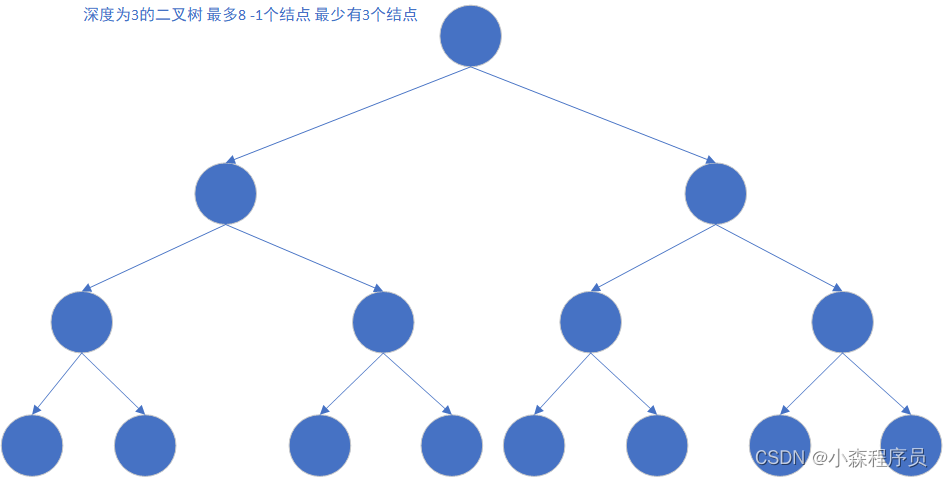
    在这里插入图片描述

  • 深度为h-1的二叉树 最多有二的h次方 -1个结点 最少有h个结点

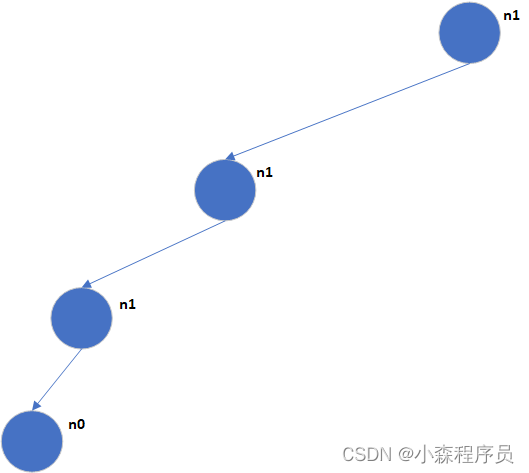
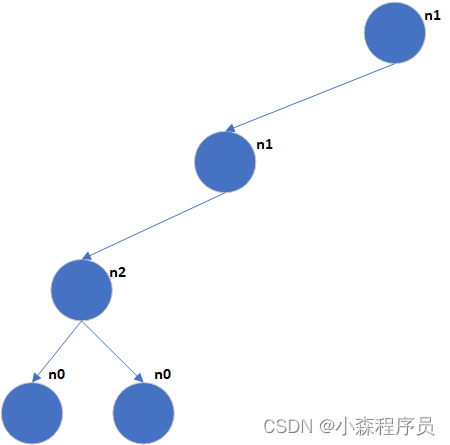
在这里插入图片描述

在这里插入图片描述

  • 对任意一颗二叉树 若叶子节点的数量表示为N0 而度数为二的树数量 为表示为N2 则 N0=N2+1;
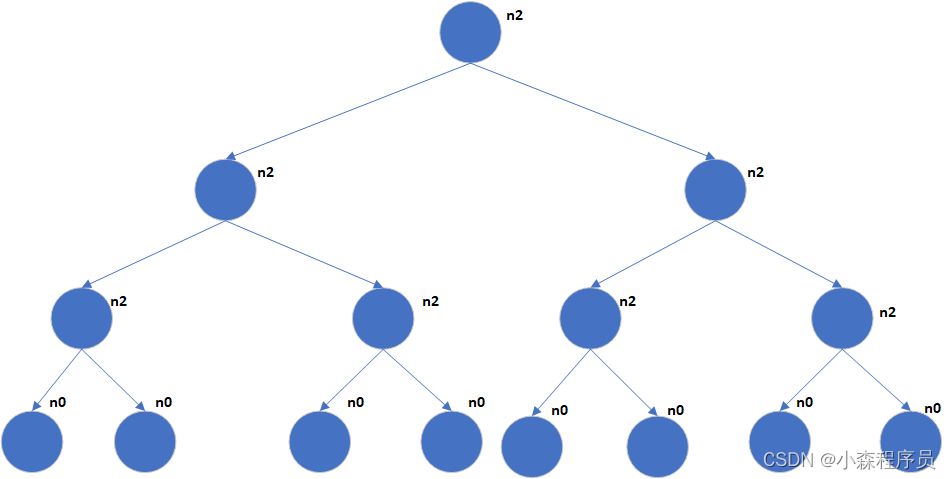
    在这里插入图片描述

若像单传那样n2=0 n1表示单传 根节点 只有一个子节点
,若其中有一个有俩节点 则n2+1;

在这里插入图片描述

在这里插入图片描述

常见二叉树分类

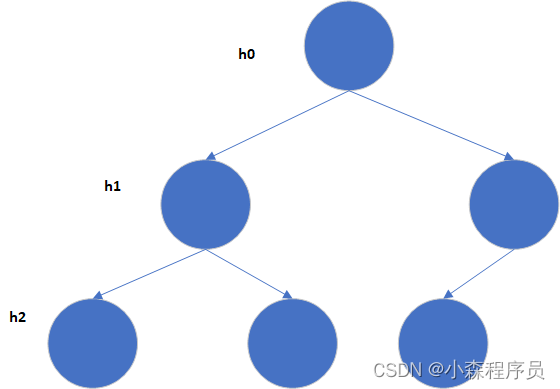
完全二叉树

  • 最后一层的最后一个节点 可有可无 其他的都是满的 才叫 完全二叉树:
    • 叶子节点必须从左到右排列 右子树的叶子节点 必须右缺 不能左缺

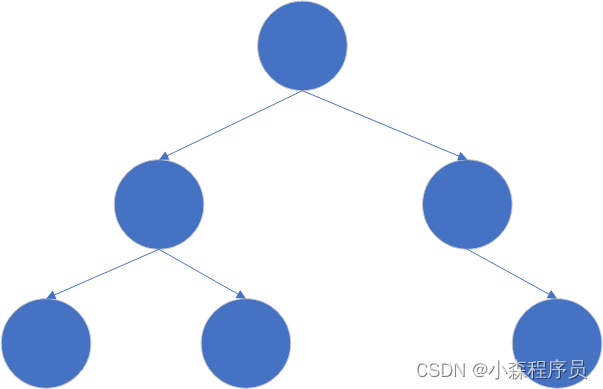
在这里插入图片描述

错误的完全二叉树:
在这里插入图片描述

完全二叉树的应用:堆

满二叉树

  • 也就是叶子结点全部都存在
    • ,并且左子树和右子树都必须是满

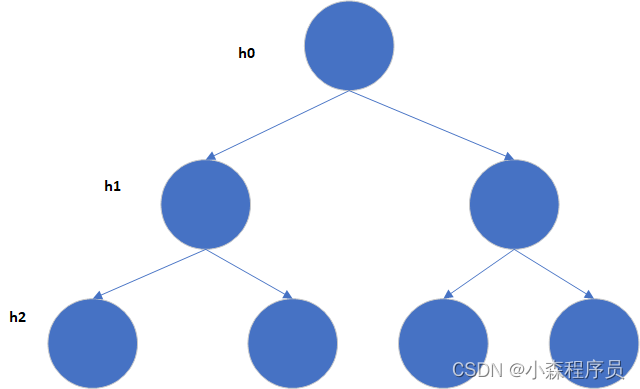
在这里插入图片描述

平衡二叉树

  • 树的两个子树的高度差绝对值不能超过1
    • 而且还得看 左右子树的两个子树的高度差绝对值不能超过1
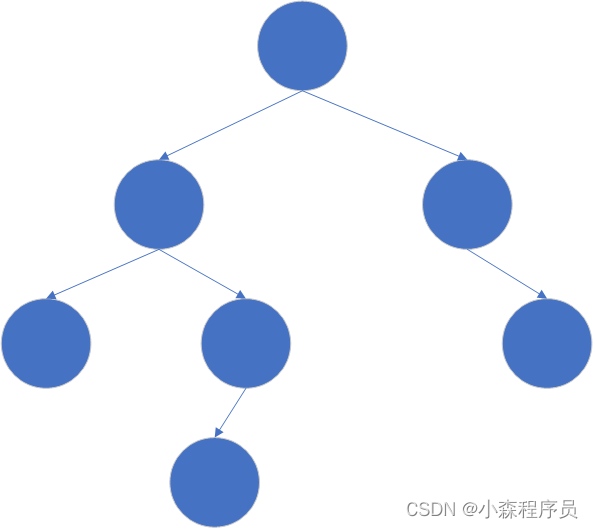
      在这里插入图片描述

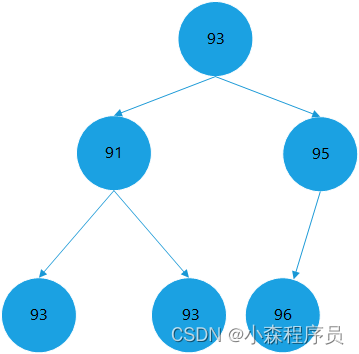
二叉搜索树

  • 二叉搜索树 也叫二叉排序树
    • 若左子树不为空 左子树均小于或者等于根节点
    • 若右子树不为空 右子树均大于或者等于根节点
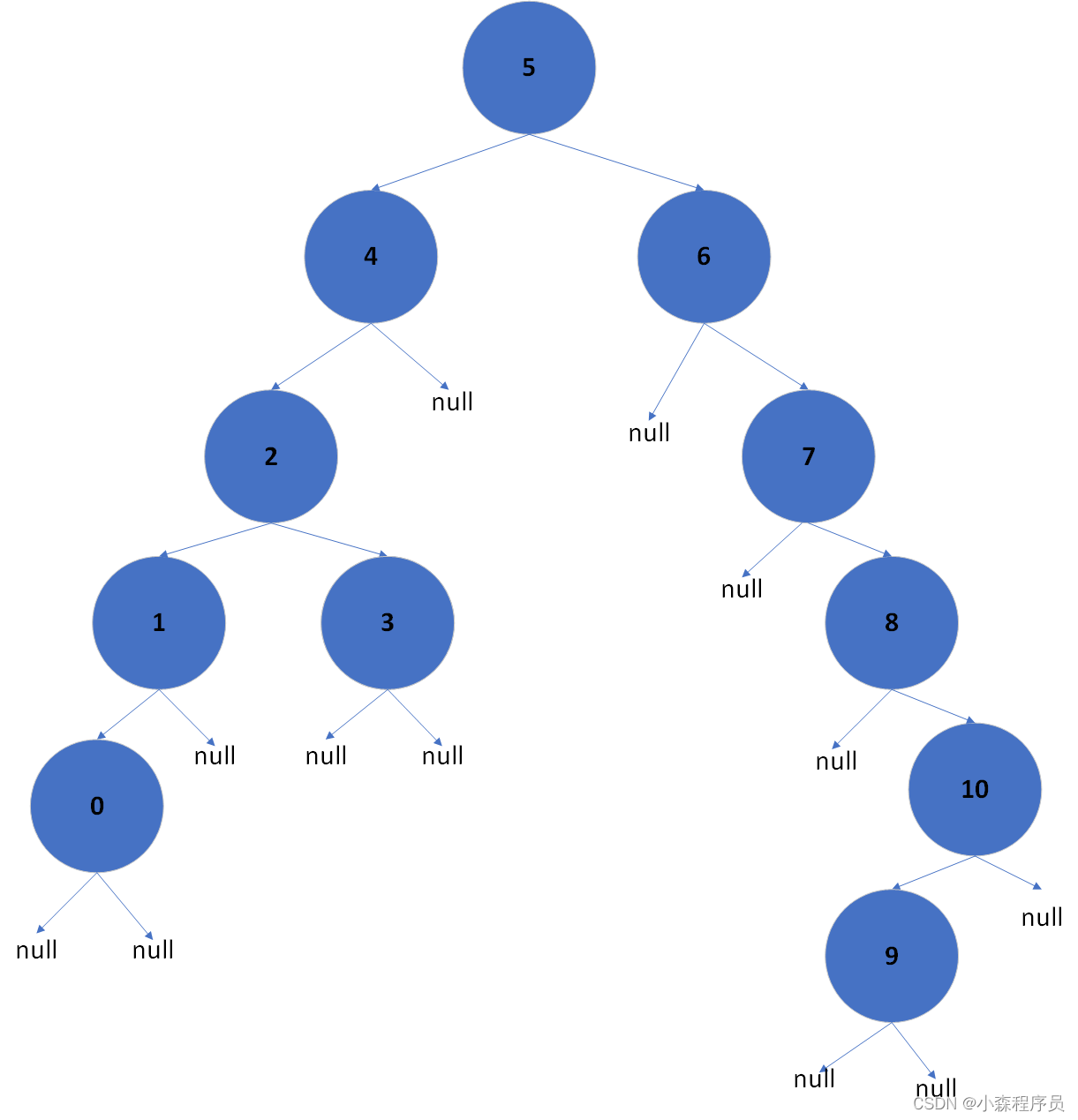
      在这里插入图片描述

红黑树

  • 带有颜色属性的平衡二叉搜索树

    • 节点的颜色属性是黑色或者红色
    • 根节点是黑色
    • 所有的叶子节点都是黑色
    • 每个红色节点必须有两个黑色节点
    • 黑色节点的子节点可红可黑
    • 红色节点的子节点必须是黑色节点

注意:不允许红色节点拥有两个连续红色子节点
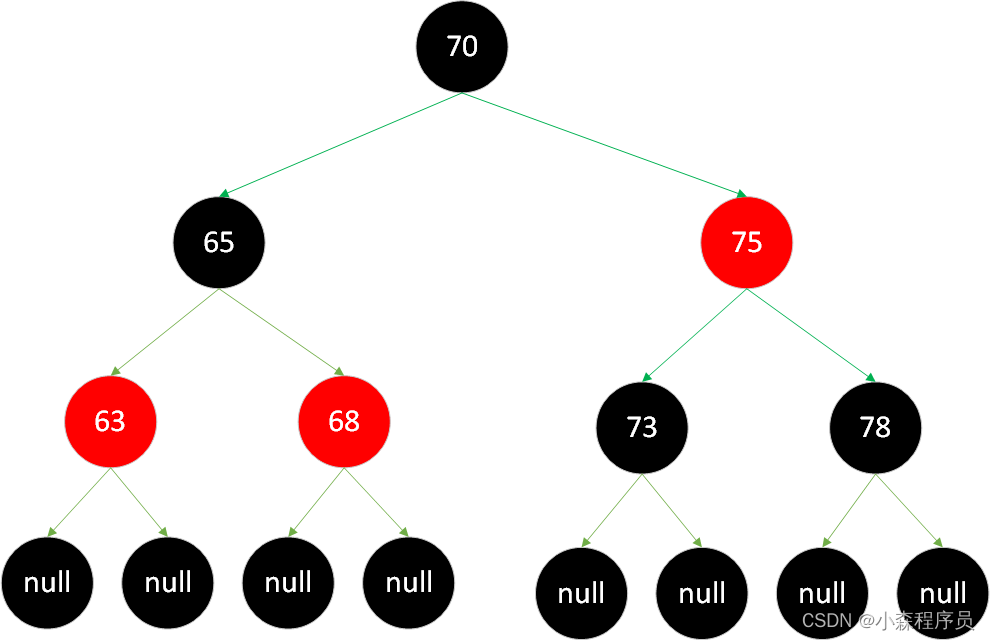
在这里插入图片描述

  • 错误的红黑树
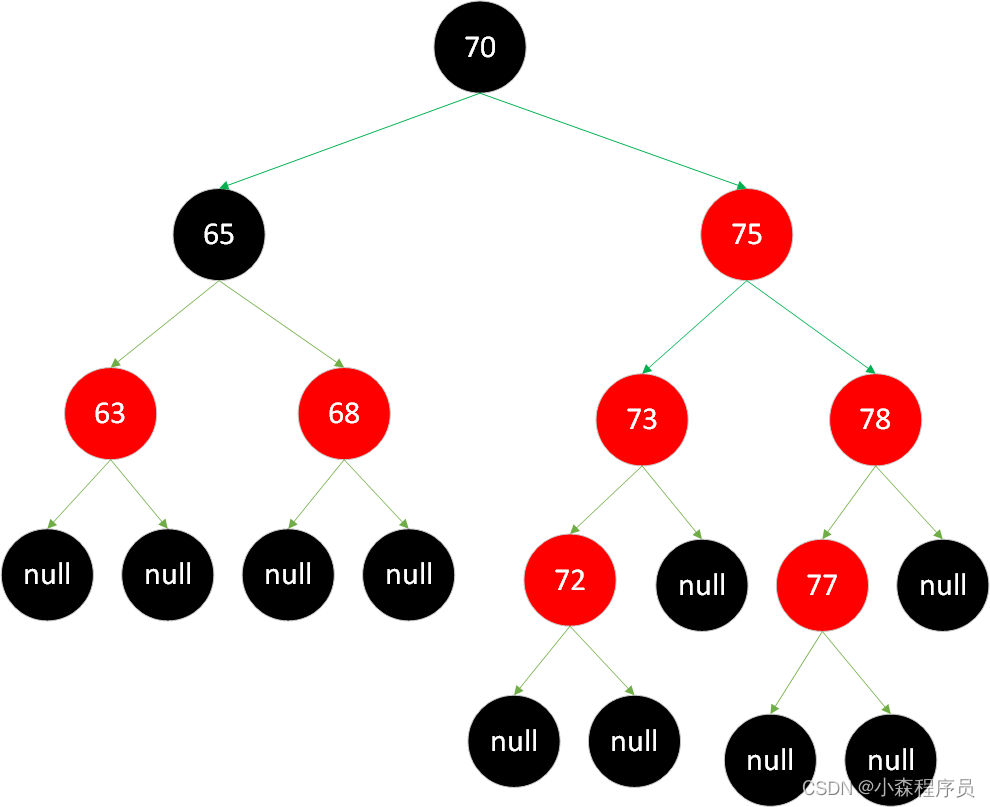
    在这里插入图片描述

  • 从任何非叶子节点到其每个叶子节点的所有简单路径都包含相同数目黑色节点

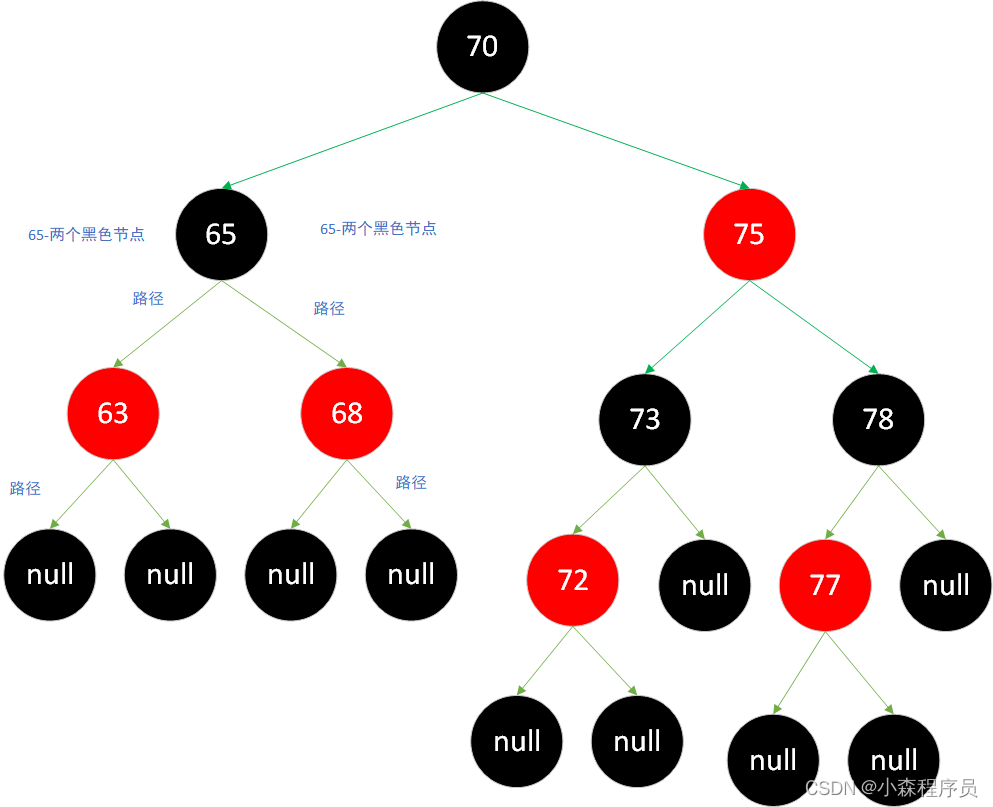
在这里插入图片描述

  • 右子树比左子树 的数目多出两倍

  • 不同的黑色节点 添加一个红色节点

为啥使用二叉搜索树

就像是电商里商品价格如下:
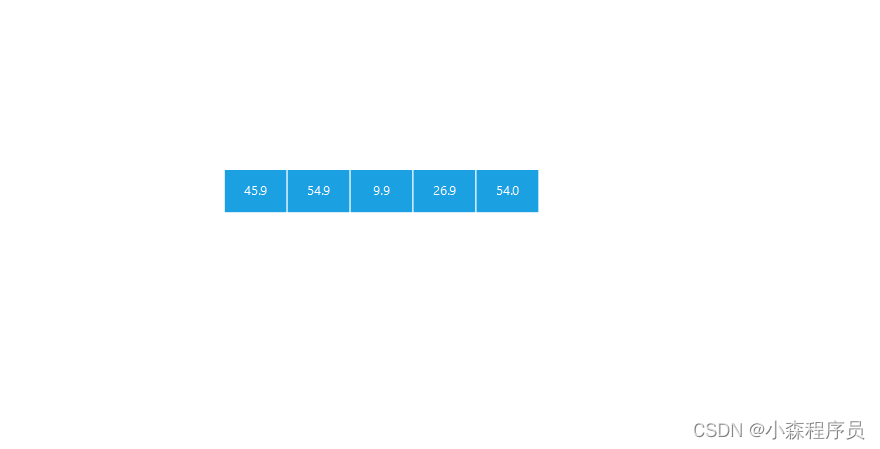
在这里插入图片描述

如果挨个去查找 9.9 元的 小零食效率很显然 ,现在很明显是在第2位置 如何大大的提高呢

先排序 价格 再来查找 你会发现不一样的美观 强迫症患者的福报,简直是

经过排序:
在这里插入图片描述

再用二分查找算法 怎么一查找就非常快 , 原理非常简单 就是从中间开始,如果 查找值 这个中间的比要小 那么排除中间+的数据 直接往左 直到找到 为止,否则往右查找

二叉搜索树 就是非常符合查找数据 而且 也是两个分支一个左,右分支

也非常复合人的特征 大脑分为左,右脑 ,手分为左,右手 脚分为左,右脚

二叉搜索树存储方式

那采用什么方式存储,如果是用顺序存储二叉树 那就是堆 ?

存储方式:链式存储
二叉搜索树节点 在这里插入图片描述
这个二叉搜索树和链表不一样 很明显 在这里LeftChild,RightChild 分别指向会 LeftChild,RightChild 分支 在二叉树的描述…

二叉搜索树算法

二叉搜索树的结构

using TreeKey = user defined;
// 树节点 = 二叉搜索树节点
using TreeNode = struct _BinarySearchTreeNode;

struct _BinarySearchTreeNode{
	TreeKey value;//tree value
	TreeNode* LeftChild;//左孩子
	TreeNode* RightChild;//右孩子
};
//二叉搜索树
struct BinarySearchTree {
	TreeNode* Root;//树的根节点
	size_t size;// 二叉搜索树的节点个数
};

二叉搜索树算法声明

#ifndef __BINARY_SEARCH_TREE_H__
#define	__BINARY_SEARCH_TREE_H__

using TreeKey = = user defined;;
using TreeNode = struct _BinarySearchTreeNode;

struct _BinarySearchTreeNode{
	TreeKey value;
	TreeNode* LeftChild;
	TreeNode* RightChild;
};

struct BinarySearchTree {
	TreeNode* Root;//树的根节点
	size_t size;// 二叉搜索树的节点个数
};

//查找当前结点中最大或者最小值
struct FindCurrentNodeMaxOrMinValue{

	TreeKey* MaxOrnMinValue;
	bool isExist;
}; 

//查找二叉搜索树结点 类型
struct FindTreeNode_type {

	TreeNode* Node;
	bool isExist;
};

//查找二叉搜索树value类型
struct FindTreeValue_type {

	TreeKey* value;
	bool isExist;
};


//二叉搜索树删除算法类型
enum class BinarySearchTreeDeletionAlgorithmType{

	Loop,//用循环来删除
	Recursive, //用递归来删除
};


//二叉搜索树删除算法类型
using BSTDeleteAlgorithmType = BinarySearchTreeDeletionAlgorithmType;


//二叉搜索树查找算法类型
enum class BinarySearchTreeSearchAlgorithmType {

	Loop,//用循环来查找
	Recursive, //用递归来查找
};

//二叉搜索树查找算法类型
using BSTSearchAlgorithmType = BinarySearchTreeSearchAlgorithmType;

//二叉搜索树遍历算法类型
enum class  BinarySearchTreeTraversalAlgorithmType {
	Recursive,
	NoRecursive
};
//二叉搜索树遍历算法类型
using BSTTraversalAlgorithmType = BinarySearchTreeTraversalAlgorithmType;

//初始化二叉搜索树
void InitBinarySearchTree(BinarySearchTree& Tree, TreeNode  * const &InitRoot = nullptr);


//初始化二叉搜索树
void  BinarySearchTree_Build(BinarySearchTree& Tree, const TreeKey* const array,  int arraySize);

//插入数据到二叉搜索树
void BinarySearchTree_Insert(BinarySearchTree& tree, const TreeKey& value);

//从二叉搜索树中删除指定的元素
bool BinarySearchTree_Erase(BinarySearchTree& tree, const TreeKey& Key, BSTDeleteAlgorithmType Defaultdelete = BSTDeleteAlgorithmType::Loop);

//二叉搜索树搜索指定元素
FindTreeValue_type BinarySearchTree_Search(BinarySearchTree& tree, const TreeKey& Key,  BSTSearchAlgorithmType DefaultSearch = BSTSearchAlgorithmType::Loop);

//先序遍历
void FirstOrderTraversal(BinarySearchTree& tree, BSTTraversalAlgorithmType DefaultTraversal= BSTTraversalAlgorithmType::NoRecursive);

//中序遍历
void InOrderTraversal(BinarySearchTree& tree, BSTTraversalAlgorithmType DefaultTraversal = BSTTraversalAlgorithmType::NoRecursive);

//后序遍历
void LastOrderTraversal(BinarySearchTree& tree, BSTTraversalAlgorithmType DefaultTraversal = BSTTraversalAlgorithmType::NoRecursive);

//层序遍历
void LevelOrderTraversal(BinarySearchTree& tree);

//销毁二叉搜索树
void DestroyBinarySearchTree(BinarySearchTree& tree);
//按照值查找节点
FindTreeNode_type BinarySearchTree_FindTreeNode(TreeNode*& RootNode, const TreeKey& Key);
//按照值查找当前节点的父节点
FindTreeNode_type BinarySearchTree_FindTreeParentNode(TreeNode*& RootNode, const TreeKey& Key);

// 查找当前节点最大值或者最小值
FindCurrentNodeMaxOrMinValue BinarySearchTree_FindMaxOrMinValue(TreeNode*& Currentnode);
#endif

二叉搜索树初始化

void InitBinarySearchTree(BinarySearchTree& Tree, TreeNode* const& InitRoot){

	Tree.Root = InitRoot;
	Tree.size = 0u;
}

二叉搜索树构建算法

void  BinarySearchTree_Build(BinarySearchTree& Tree, const TreeKey *const array, int arraySize){
	
	
	if (arraySize>0 && array)	{

		InitBinarySearchTree(Tree);
		auto First = array;
		auto Last = array + arraySize;

		while (First!=Last){
			auto &value = *First++;
			BinarySearchTree_Insert(Tree, value);
		}

	}
}

二叉搜索树插入算法

思维导图

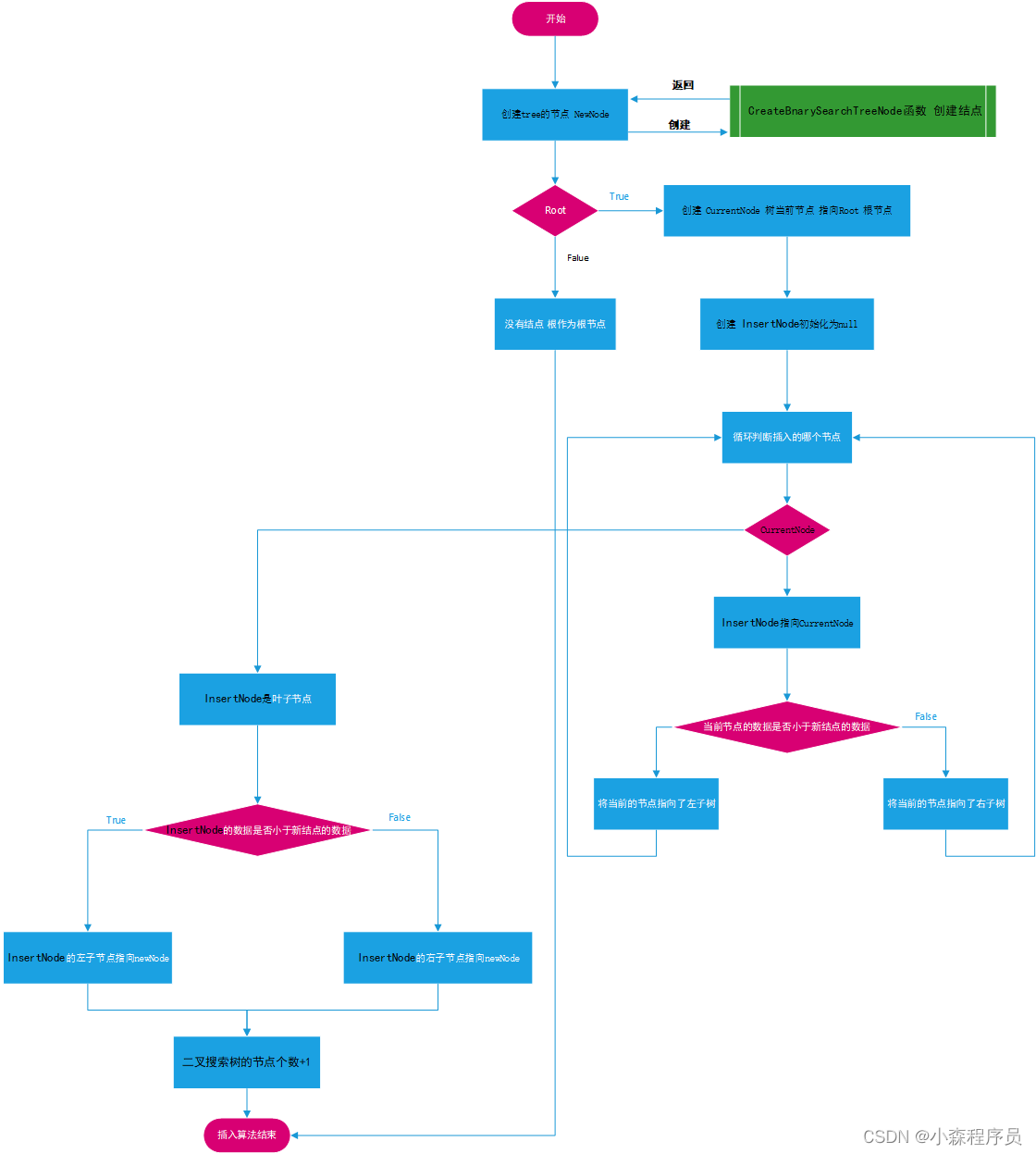
在这里插入图片描述

流程图

在这里插入图片描述

void BinarySearchTree_Insert(BinarySearchTree & tree, const TreeKey & value) {

	//创建二叉树搜索树节点
	TreeNode* newTreeNode = CreateBnarySearchTreeNode(value);
	//判断是否是空树 树根节点是不是空
	const bool  isRootNodeEmpty = tree.Root;
	if (!isRootNodeEmpty) {
		tree.Root = newTreeNode;
	}

	TreeNode* currentNode = tree.Root;

	if (isRootNodeEmpty) {

		TreeNode* InsertNode = nullptr;
		while (currentNode) {
			InsertNode = currentNode;
			if (newTreeNode->value < currentNode->value) {

				currentNode = currentNode->LeftChild;
			}
			else {
				currentNode = currentNode->RightChild;
			}
		}

		const bool isLertInsert = newTreeNode->value < InsertNode->value;

		if (isLertInsert) {
			InsertNode->LeftChild = newTreeNode;
		}
		else {
			InsertNode->RightChild = newTreeNode;
		}

	}

	++tree.size;

}

二叉搜索树删除算法

通过递归

递归删除算法图

在这里插入图片描述

递归删除二叉搜索树的节点算法

static  FindCurrentNodeMaxOrMinValue BinarySearchTree_FindMax(TreeNode*& Currentnode) {
	FindCurrentNodeMaxOrMinValue find{ 0 };
	TreeNode* CurrentNode = Currentnode;
	if (CurrentNode) {
		if (CurrentNode->RightChild) {
			CurrentNode = CurrentNode->RightChild;

			find = { &CurrentNode->value ,(bool)CurrentNode };
		}
	}
	return find;
}

static TreeNode* Recursive_EraseTreeNode(TreeNode* &Root, const TreeKey& Key, TreeNode*& deleteNode) {

	if (!Root){
		return nullptr;
	}

	if (Root->value > Key) {
		Root->LeftChild = Recursive_EraseTreeNode(Root->LeftChild, Key, deleteNode);
		return Root;
	}
	if (Root->value < Key) {
		Root->RightChild = Recursive_EraseTreeNode(Root->RightChild, Key, deleteNode);
		return Root;
	}
	deleteNode = Root;

	if (!Root->LeftChild && !Root->RightChild) {


		Root = nullptr;
		return Root;
	}

	if ((!Root->LeftChild && Root->RightChild)) {

		return Root->RightChild;

	}

	if (Root->LeftChild && !Root->RightChild) {

		return Root->LeftChild;
	}

	auto FIndRet = BinarySearchTree_FindMax(Root);
	if (FIndRet.isExist){
		Root->value = *FIndRet.MaxOrnMinValue;
	}

	Root->RightChild = Recursive_EraseTreeNode(Root->RightChild, *FIndRet.MaxOrnMinValue, deleteNode);
	return Root;
}

通过循环

bool IsSame(TreeNode*& Target, TreeNode*& Source) {
	return Target == Source;
 }

void DestroyTreeNode(TreeNode*& treeNode,  const  TreeNode*const &where = nullptr) {
	delete treeNode;
	treeNode = (decltype(treeNode))where;
}

void  unlinkTreeNodeLeftChild(TreeNode*& TargetNode, TreeNode* SourceNode=nullptr) {
	TargetNode ? TargetNode->LeftChild = SourceNode : TargetNode;
}

void unlinkTreeNodeRightChild(TreeNode*& TargetNode,  TreeNode * SourceNode = nullptr) {
	TargetNode ?  TargetNode->RightChild= SourceNode : TargetNode;
}

FindTreeNode_type BinarySearchTree_FindTreeNode(TreeNode*& RootNode, const TreeKey& Key){

	FindTreeNode_type FindRet{ 0 };
	auto currentNode = RootNode;
	if (currentNode) {

		while (currentNode && currentNode->value != Key) {
			if (!(Key < currentNode->value) ){
				currentNode = currentNode->RightChild;
			}
			else {
				currentNode = currentNode->LeftChild;
			}
		}
		if (currentNode) {

			FindRet = { currentNode,(bool)currentNode };

		}
	}

	return FindRet;
}

FindTreeNode_type BinarySearchTree_FindTreeParentNode(TreeNode*& RootNode, const TreeKey& Key) {

	FindTreeNode_type FindRet{ 0 };
	auto currentNode = RootNode;
	if (currentNode) {
		FindRet.isExist = true;
		while (currentNode && currentNode->value != Key) {
			FindRet.Node = currentNode;

			if (currentNode->value > Key) {
				currentNode = currentNode->LeftChild;
			}
			else {
				currentNode = currentNode->RightChild;
			}
		}
		FindRet.isExist = currentNode != nullptr ? FindRet.isExist : !FindRet.isExist;
	}

	return FindRet;
}

FindCurrentNodeMaxOrMinValue BinarySearchTree_FindMaxOrMinValue(TreeNode*& Currentnode){
	FindCurrentNodeMaxOrMinValue find{ 0 };
	TreeNode* CurrentNode = Currentnode;
	if (CurrentNode)	{
		if (CurrentNode->LeftChild){
			CurrentNode = CurrentNode->LeftChild;
			while (CurrentNode->RightChild){
			CurrentNode = CurrentNode->RightChild;
			}
			find = { &CurrentNode->value ,(bool)CurrentNode };
		}
		 
		else if (CurrentNode->RightChild) {
		
			CurrentNode = CurrentNode->RightChild;

			while (CurrentNode->LeftChild){
				CurrentNode = CurrentNode->LeftChild;
			}

			find = { &CurrentNode->value ,(bool)CurrentNode };
		}
	}
	return find;
}

bool Loop_EraseTreeNode(BinarySearchTree& tree, const TreeKey& Key) {
	

	FindTreeNode_type FindCurrent = BinarySearchTree_FindTreeNode(tree.Root, Key);
	FindTreeNode_type FindCurrentParent = BinarySearchTree_FindTreeParentNode(tree.Root, Key);

	if (FindCurrent.isExist) {

		if (!FindCurrent.Node->LeftChild && !FindCurrent.Node->RightChild) {
			if (!IsSame(FindCurrent.Node, tree.Root)) {
				if (FindCurrentParent.isExist) {

					if (IsSame(FindCurrentParent.Node->LeftChild, FindCurrent.Node)) {
						unlinkTreeNodeLeftChild(FindCurrentParent.Node);
					}
					else {
						unlinkTreeNodeRightChild(FindCurrentParent.Node);
					}
				}
			}
			else {
				tree.Root = nullptr;
			}

			DestroyTreeNode(FindCurrent.Node);

		}
		else if (FindCurrent.Node->LeftChild && !FindCurrent.Node->RightChild) {

			if (!IsSame(FindCurrent.Node, tree.Root)) {
				if (FindCurrentParent.isExist) {

					if (IsSame(FindCurrentParent.Node->LeftChild, FindCurrent.Node)) {
						FindCurrentParent.Node->LeftChild = FindCurrent.Node->LeftChild;
					}
					else{
						FindCurrentParent.Node->RightChild = FindCurrent.Node->LeftChild;
					}
					unlinkTreeNodeLeftChild(FindCurrent.Node);
				}
			}

			else {
				(tree.Root = tree.Root->LeftChild);
			}
			DestroyTreeNode(FindCurrent.Node);
		}
		else if (FindCurrent.Node->RightChild && !FindCurrent.Node->LeftChild) {

			if (!IsSame(FindCurrent.Node, tree.Root)) {
				if (FindCurrentParent.isExist) {

					if (IsSame(FindCurrentParent.Node->LeftChild, FindCurrent.Node)) {
						(FindCurrentParent.Node->LeftChild = FindCurrent.Node->RightChild);
					}
					else {
						(FindCurrentParent.Node->RightChild = FindCurrent.Node->RightChild);
					}
					unlinkTreeNodeRightChild(FindCurrent.Node);
				}
			}
			else {
				(tree.Root = tree.Root->RightChild);
			}
			
			DestroyTreeNode(FindCurrent.Node);
		}
		else{
			auto MaxOrMinKey = BinarySearchTree_FindMaxOrMinValue(FindCurrent.Node);
			FindTreeNode_type DeleteCurrent = BinarySearchTree_FindTreeNode(tree.Root, *MaxOrMinKey.MaxOrnMinValue);
			FindTreeNode_type DeleteCurrentParent = BinarySearchTree_FindTreeParentNode(tree.Root, *MaxOrMinKey.MaxOrnMinValue);
			FindCurrent.isExist = MaxOrMinKey.isExist;
			if (FindCurrent.isExist){
				
				FindCurrent.isExist = DeleteCurrentParent.Node;
				FindCurrent.Node->value = *MaxOrMinKey.MaxOrnMinValue;
				if (FindCurrent.isExist){
					if (IsSame(DeleteCurrentParent.Node->LeftChild, DeleteCurrent.Node)){
						if (DeleteCurrent.Node->RightChild && !DeleteCurrent.Node->LeftChild) {
							(DeleteCurrentParent.Node->LeftChild = DeleteCurrent.Node);
						}
						else{
							unlinkTreeNodeLeftChild(DeleteCurrentParent.Node);
						}
					}
					else if (IsSame(DeleteCurrentParent.Node->RightChild, DeleteCurrent.Node)){
						if (DeleteCurrent.Node->LeftChild && !DeleteCurrent.Node->RightChild){
							(DeleteCurrentParent.Node->LeftChild = DeleteCurrent.Node->LeftChild);
						}
						else {
							unlinkTreeNodeRightChild(DeleteCurrentParent.Node);
						}
					}

					unlinkTreeNodeLeftChild(DeleteCurrent.Node);
					unlinkTreeNodeRightChild(DeleteCurrent.Node);

					DestroyTreeNode(DeleteCurrent.Node);
				}
			}

		}

		--tree.size;

	}
	return FindCurrent.isExist;
}

二叉搜索树删除算法实现

bool BinarySearchTree_Erase(BinarySearchTree& tree, const TreeKey& Key, BSTDeleteAlgorithmType Defaultdelete){
	
	bool ret = false;

	switch (Defaultdelete)	{

	case BSTDeleteAlgorithmType::Loop:
		ret = Loop_EraseTreeNode(tree, Key);
		break;
	case BSTDeleteAlgorithmType::Recursive:
		TreeNode* deleteNode = nullptr;
		Recursive_EraseTreeNode(tree.Root, Key, deleteNode);
		if (deleteNode){
			DestroyTreeNode( deleteNode);
			--tree.size;
			ret = true;
			break;
		}			
	}
	return ret;
}

二叉搜索树查找算法

通过递归

FindTreeValue_type BinarySearchTree_RecursiveSearch(TreeNode*& RootNode, const TreeKey& Key){

	FindTreeValue_type find = {};
	if (RootNode==nullptr||RootNode->value==Key)	{
		find = { RootNode ? &RootNode->value : nullptr,(bool)RootNode };
	}
	else if (Key<RootNode->value){
		find = BinarySearchTree_RecursiveSearch(RootNode->LeftChild, Key);
	}else{
		find = BinarySearchTree_RecursiveSearch(RootNode->RightChild, Key);
	}

	return find;
}

通过循环

FindTreeValue_type BinarySearchTree_LoopSearch(TreeNode*& RootNode, const TreeKey& Key){
	
		FindTreeValue_type FindRet{ 0 };
		auto currentNode = RootNode;
		if (currentNode) {

			while (currentNode && currentNode->value != Key) {
				if (currentNode->value > Key) {
					currentNode = currentNode->LeftChild;
				}
				else {
					currentNode = currentNode->RightChild;
				}
			}
			if (currentNode) {
				FindRet = { &currentNode->value,(bool)currentNode };
			}
		}

		return FindRet;
}

二叉搜索树查找算法实现

FindTreeValue_type BinarySearchTree_Search(BinarySearchTree& tree, const TreeKey& Key, BSTSearchAlgorithmType DefaultSearch){

	const  int LestIndex = (int)BSTSearchAlgorithmType::Recursive + 1;
	const decltype(&BinarySearchTree_LoopSearch)Search[LestIndex]{BinarySearchTree_LoopSearch,BinarySearchTree_RecursiveSearch };
	const int SearchIndex = (int)DefaultSearch % LestIndex;
	return Search[SearchIndex](tree.Root, Key);
	
}

二叉搜索树遍历算法

//先序遍历
void FirstOrderTraversal(BinarySearchTree& tree, BSTTraversalAlgorithmType DefaultTraversal) {

	constexpr decltype(&FirstOrderNonRecursiveTraversal) Traversal[] = { FirstOrderRecursiveTraversal,FirstOrderNonRecursiveTraversal };
	constexpr int LastIndex = sizeof(Traversal) / sizeof(*Traversal);
	const auto str = DefaultTraversal == BSTTraversalAlgorithmType::Recursive ? "递归" : "非递归";
	cout << "<" << str << "先序遍历> :";

	const int TraversalIndex = (int)DefaultTraversal % LastIndex;

	Traversal[TraversalIndex](tree.Root);

	cout << "<null>" << endl;
}
//中序遍历
void InOrderTraversal(BinarySearchTree& tree, BSTTraversalAlgorithmType DefaultTraversal) {

	constexpr decltype(&FirstOrderNonRecursiveTraversal) Traversal[] = { InOrderRecursiveTraversal,InOrderNonRecursiveTraversal };
	constexpr int LastIndex = sizeof(Traversal) / sizeof(*Traversal);

	const auto str = DefaultTraversal == BSTTraversalAlgorithmType::Recursive ? "递归" : "非递归";
	cout << "<" << str << "中序遍历> :";
	const int TraversalIndex = (int)DefaultTraversal % LastIndex;

	Traversal[TraversalIndex](tree.Root);

	cout << "<null>" << endl;
}

//后序遍历
void LastOrderTraversal(BinarySearchTree& tree, BSTTraversalAlgorithmType DefaultTraversal) {

	constexpr decltype(&LastOrderNonRecursiveTraversal) Traversal[] = { LastOrderRecursiveTraversal,LastOrderNonRecursiveTraversal };
	constexpr int LastIndex = sizeof(Traversal) / sizeof(*Traversal);

	const auto str = DefaultTraversal == BSTTraversalAlgorithmType::Recursive ? "递归" : "非递归";
	cout << "<" << str << "后序遍历> :";
	
	const int TraversalIndex = (int)DefaultTraversal % LastIndex;

	Traversal[TraversalIndex](tree.Root);

	cout << "<null>" << endl;
}

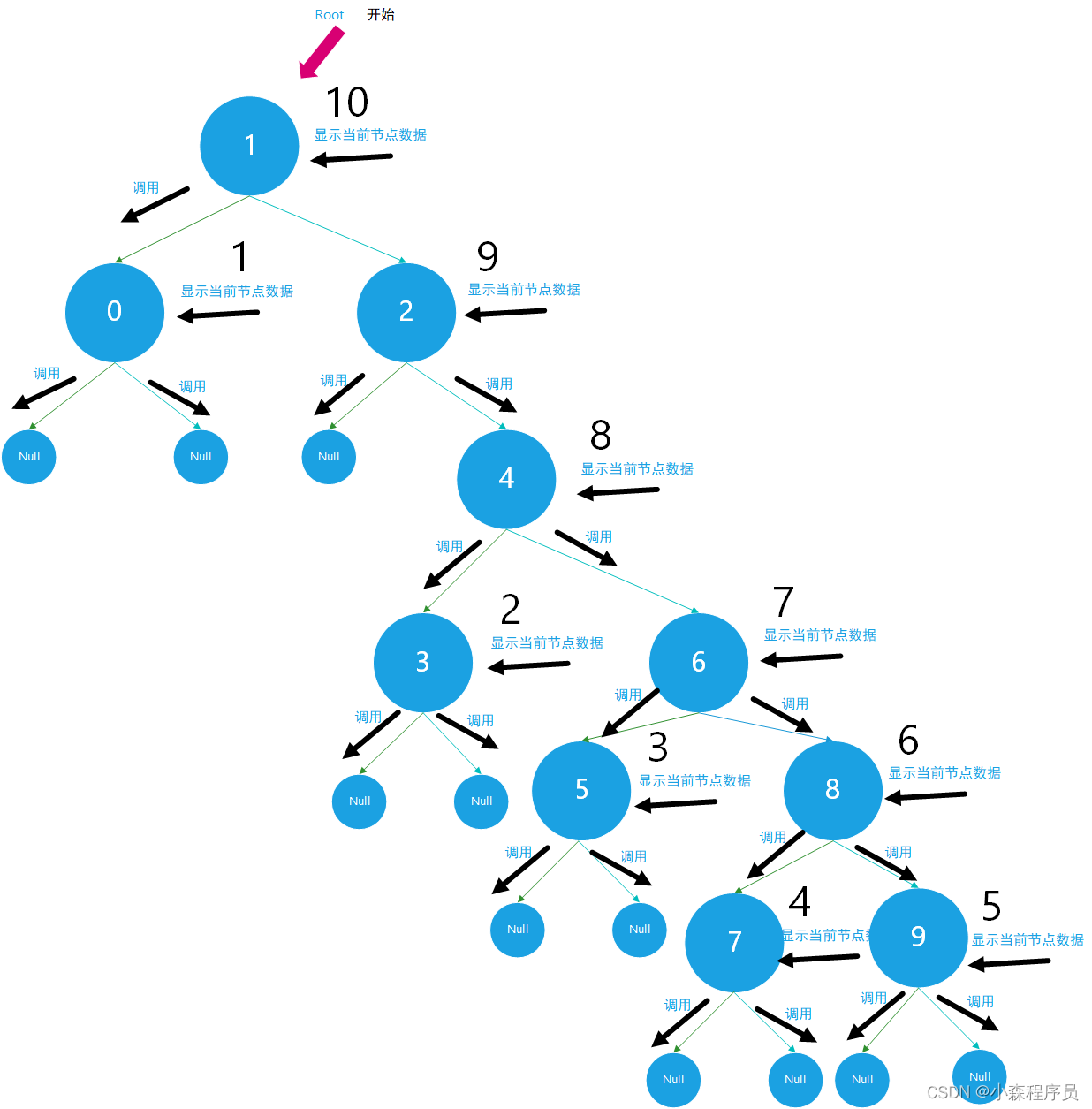
递归遍历

前序遍历

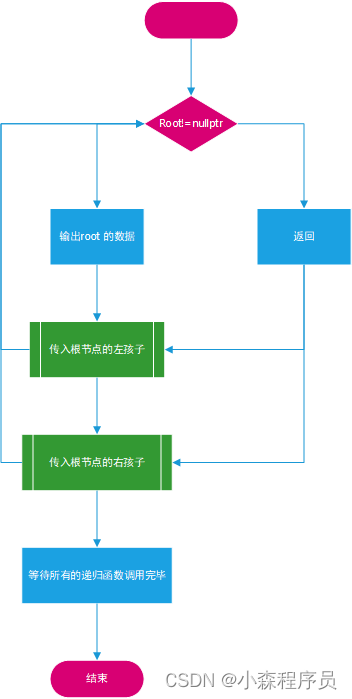
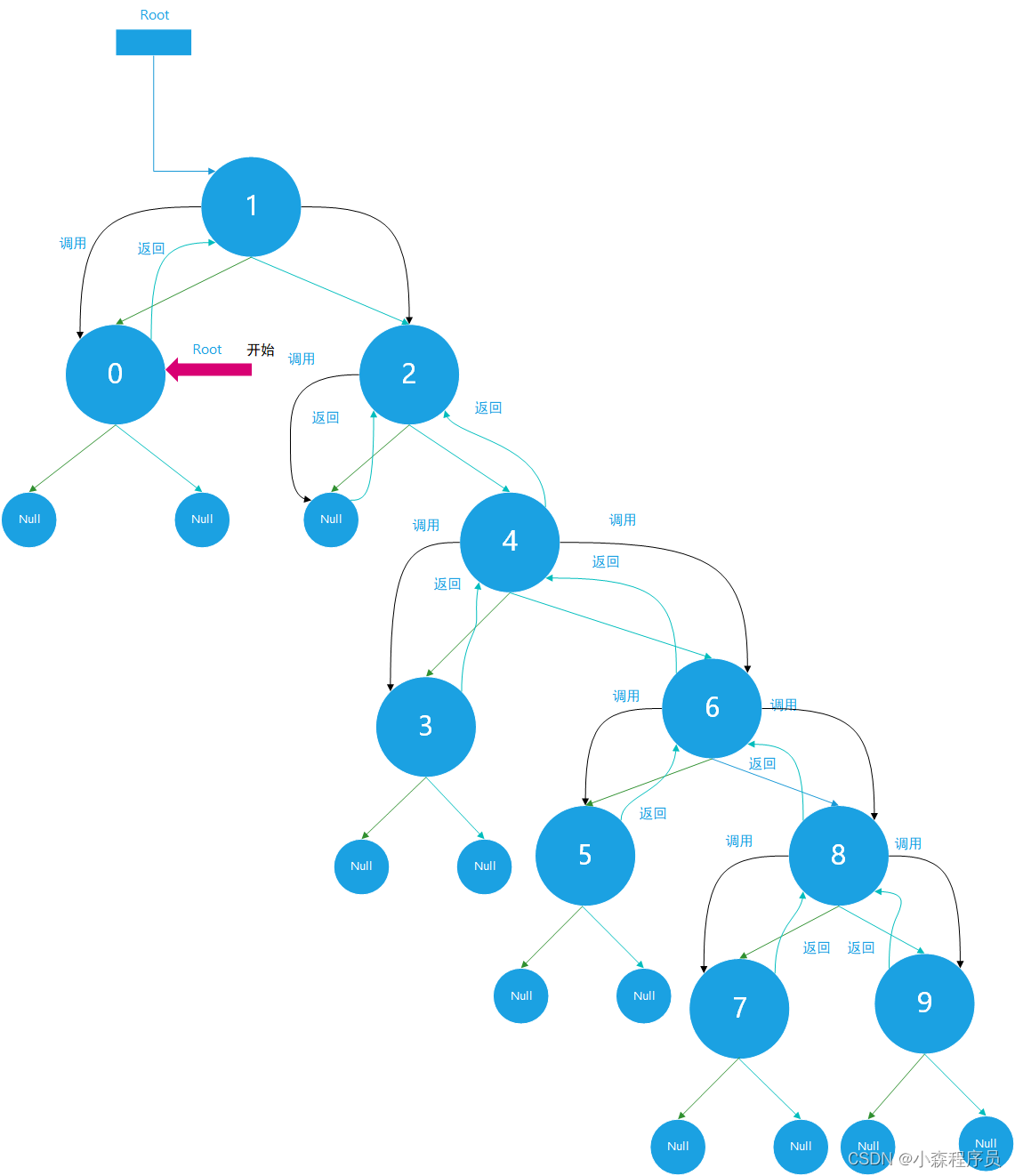
在这里插入图片描述

指定的二叉搜索树的递归遍历
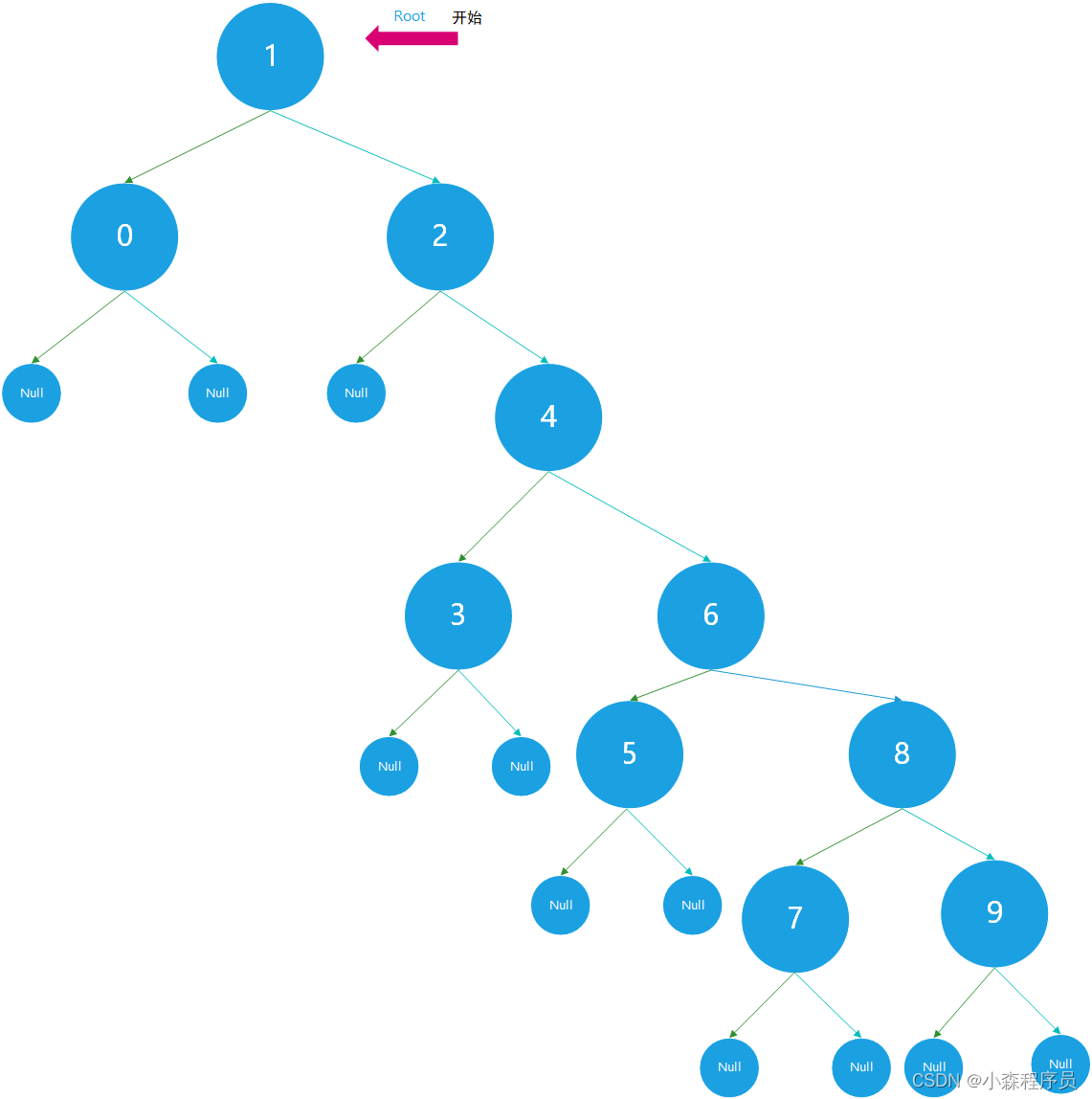
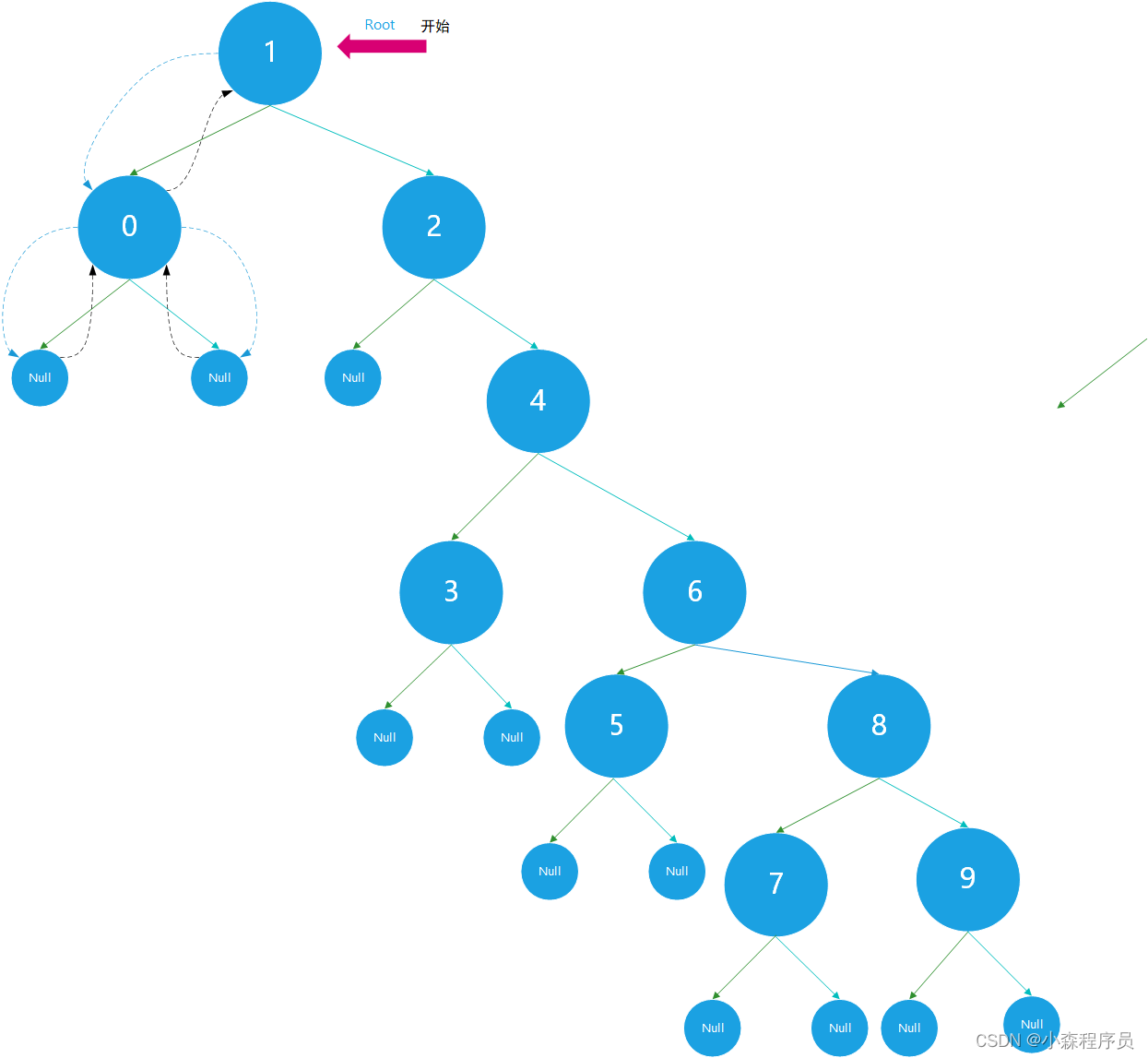
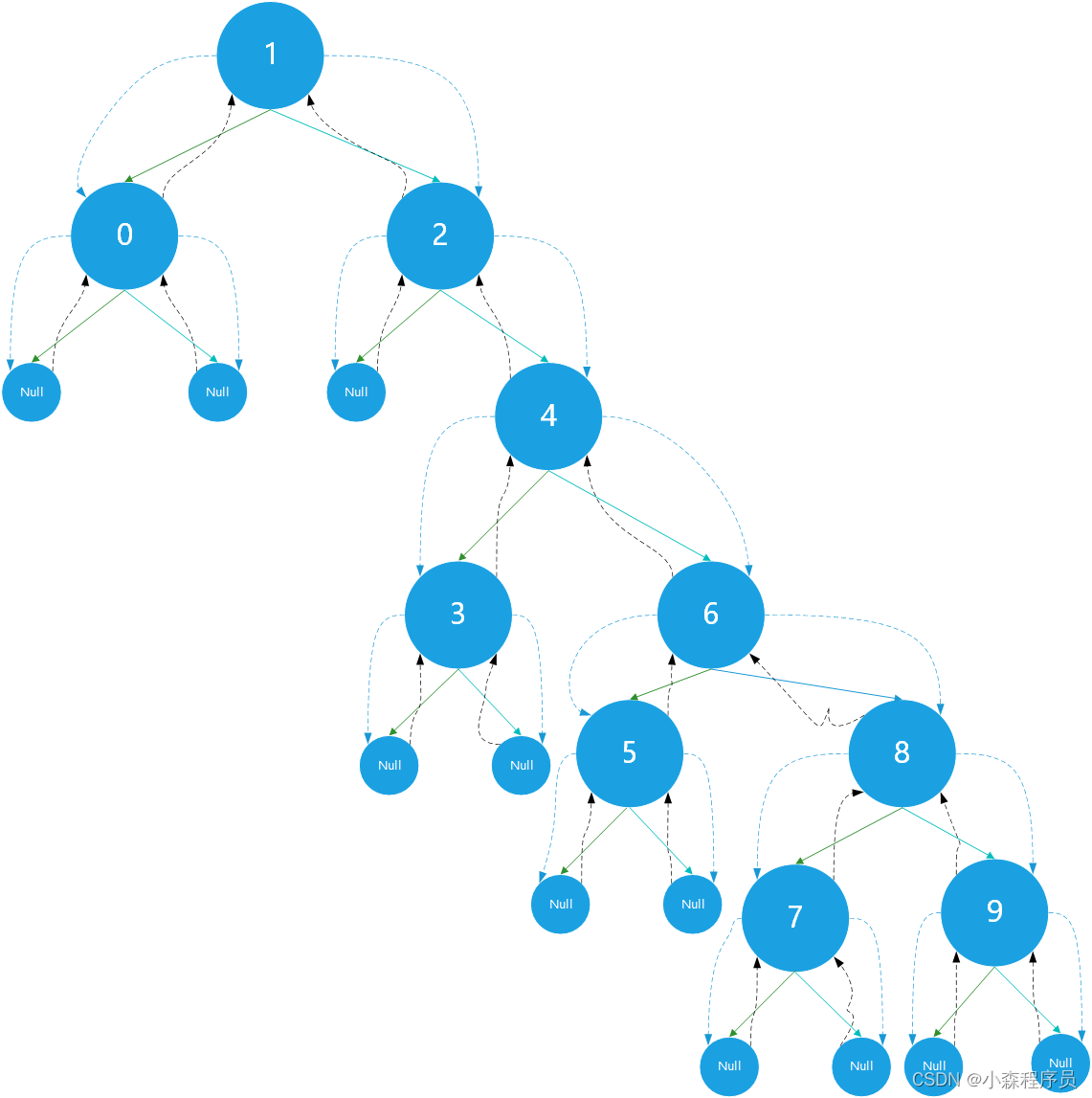
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

  1. 蓝色的虚线连接线表示:调用函数
  2. 黑色的虚线连接线表示返回到上一个结点

递归调用栈

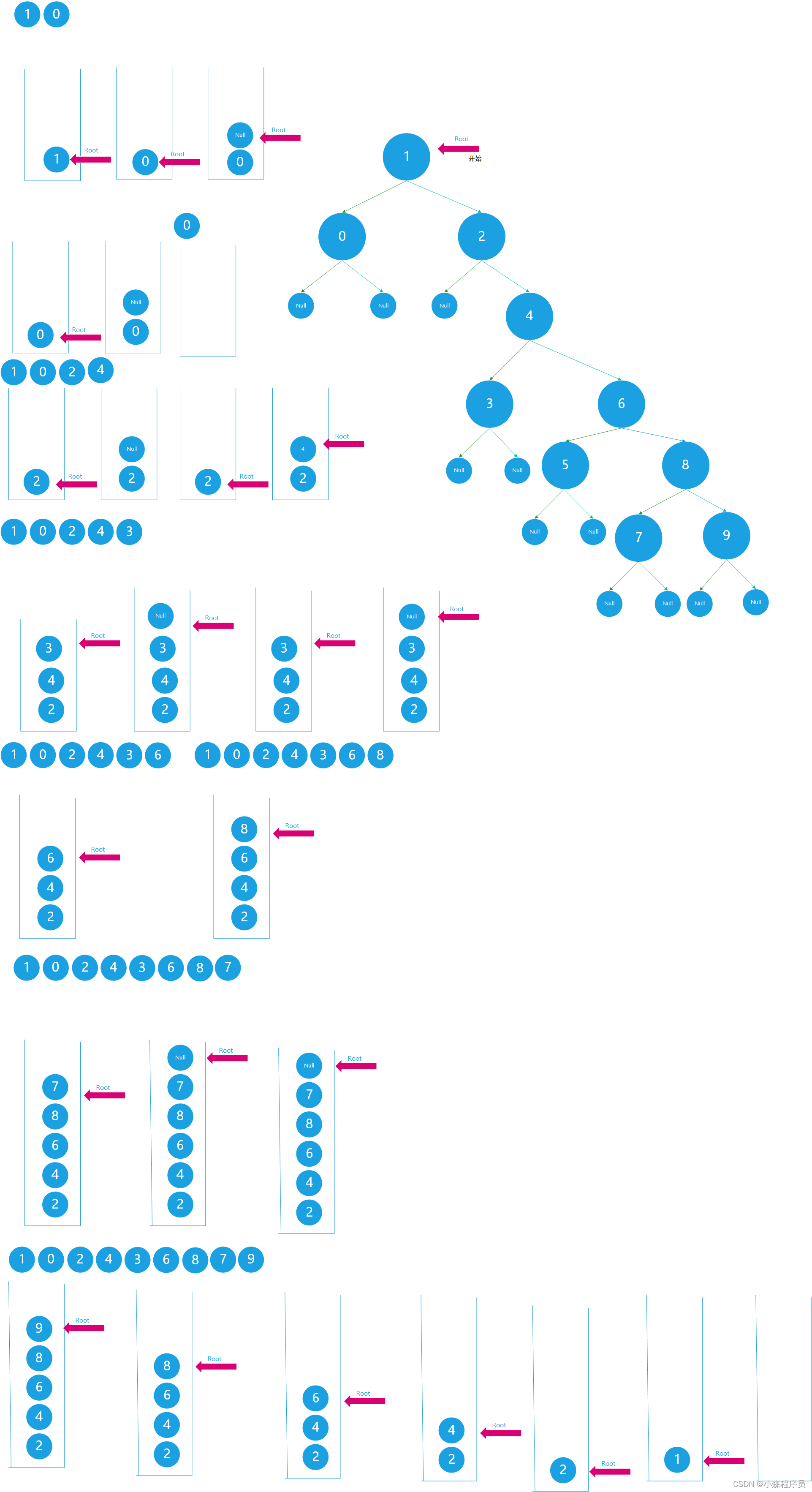
在这里插入图片描述

递归先序遍历 代码执行过程图

执行 根 和 左子树

在这里插入图片描述

执行右子树

在这里插入图片描述

执行右子树 并且返回根节点

在这里插入图片描述

先根 再左 后右 递归前序遍历顺口溜

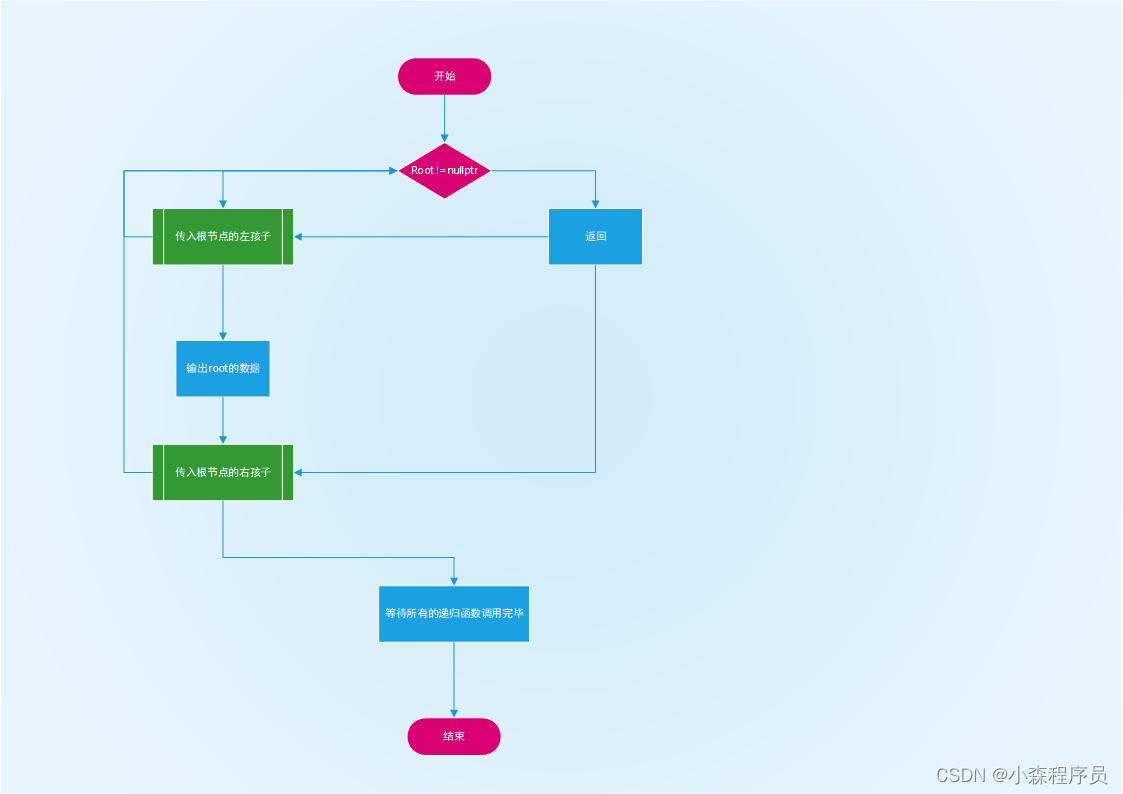
//递归前序遍历 根 -> 左 -> 右
void FirstOrderRecursiveTraversal(TreeNode*& Root) {
	if (Root) {
		cout <<" "<< Root->value << " ->";

		FirstOrderRecursiveTraversal(Root->LeftChild);
		FirstOrderRecursiveTraversal(Root->RightChild);
	}
}

中序遍历

在这里插入图片描述

指定的二叉搜索树递归遍历
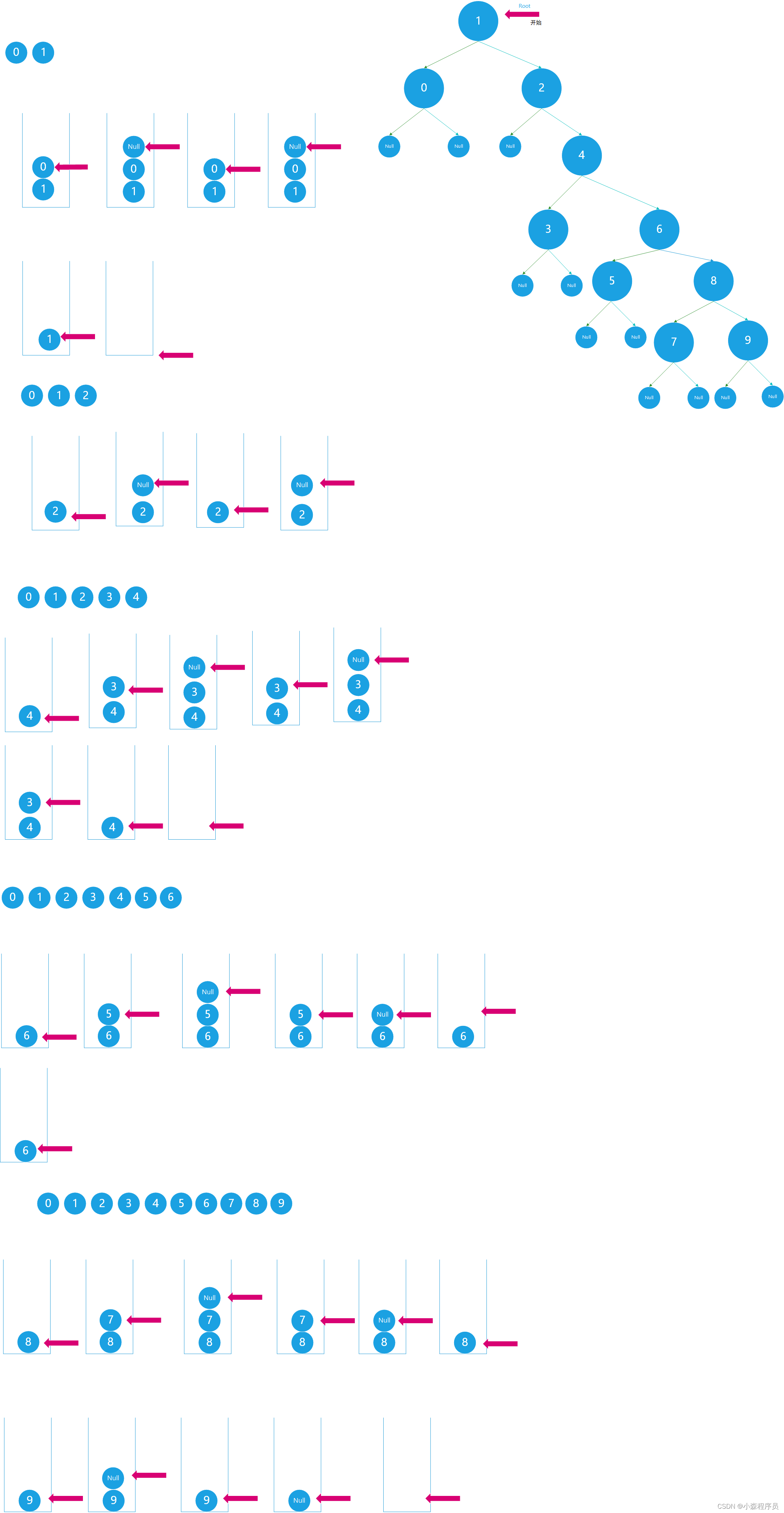
在这里插入图片描述
在这里插入图片描述

先左 再根 后右 递归中序遍历顺口溜

//递归中序遍历
void InOrderRecursiveTraversal(TreeNode*& Root) {
	if (Root) {
		InOrderRecursiveTraversal(Root->LeftChild);

		cout << " " << Root->value << " ->";

		InOrderRecursiveTraversal(Root->RightChild);
	}
}

后序遍历

在这里插入图片描述

先左 再右 后根 递归后序遍历顺口溜


//递归后序遍历
void  LastOrderRecursiveTraversal(TreeNode*& Root) {

	if (Root) {
		LastOrderRecursiveTraversal(Root->LeftChild);
		LastOrderRecursiveTraversal(Root->RightChild);
		cout << " " << Root->value << " ->";
	}
}

非递归遍历

前序遍历

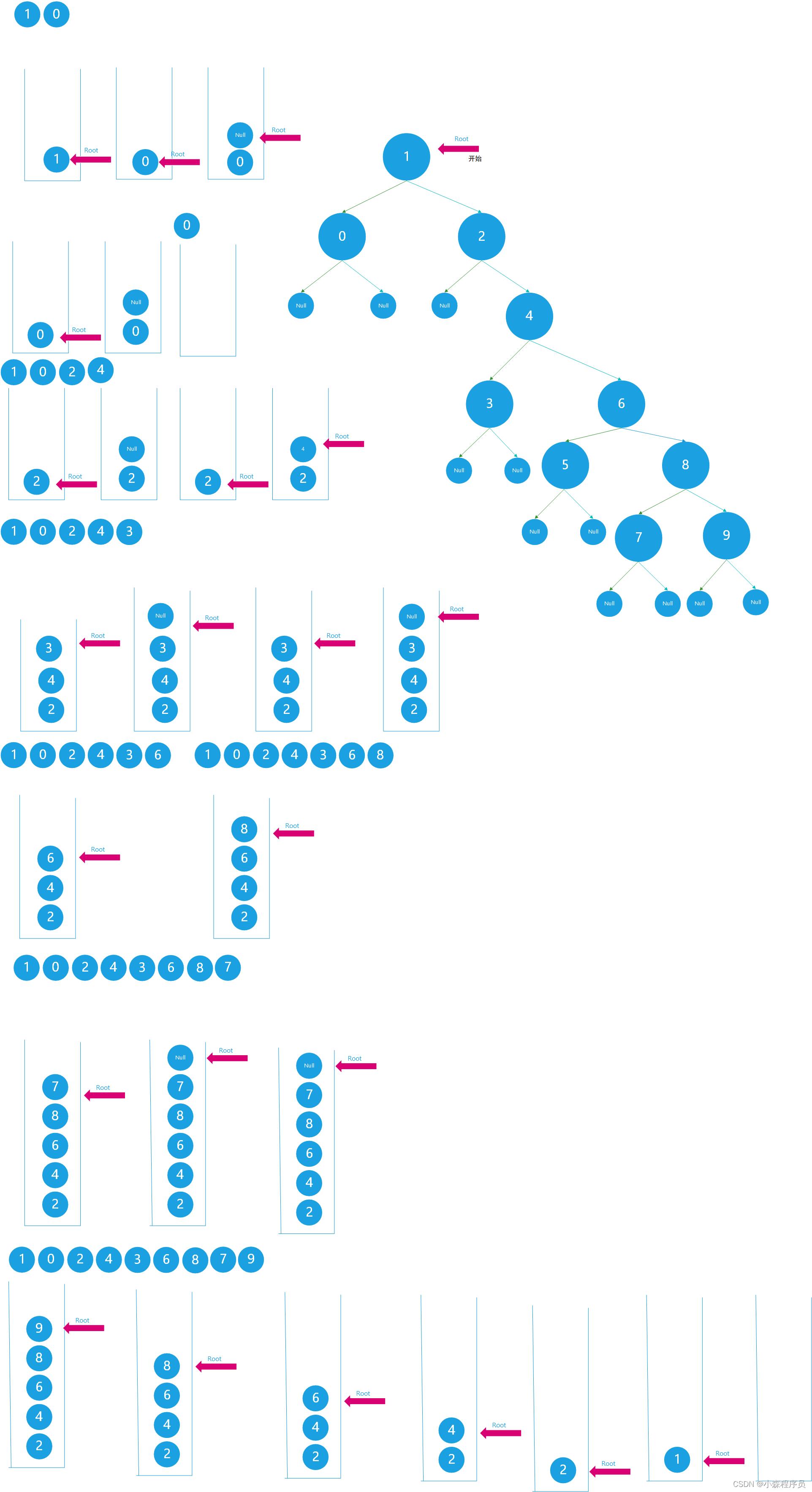
在这里插入图片描述

//非递归先序遍历
static void FirstOrderNonRecursiveTraversal(TreeNode*& Root) {

	SeqStack Stack;
	initStack(Stack);

	auto CurrentNode = Root;
	push_Stack(Stack, CurrentNode);
	while (!emptyStack(Stack)) {

		CurrentNode = TopStack(Stack);
		cout << " " << CurrentNode->value << "-> ";
		pop_Stack(Stack);
		if (CurrentNode->RightChild) {
			push_Stack(Stack, CurrentNode->RightChild);
		}
		if (CurrentNode->LeftChild) {
			push_Stack(Stack, CurrentNode->LeftChild);
		}
	}

	destroyStack(Stack);
}

中序遍历

在这里插入图片描述

//非递归中序遍历
static void InOrderNonRecursiveTraversal(TreeNode*& Root) {

	SeqStack Stack;
	initStack(Stack);
	//cout << "<中序遍历> :" 
	auto CurrentNode = Root;
	while (!emptyStack(Stack) || CurrentNode) {

		while (CurrentNode) {
			push_Stack(Stack, CurrentNode);
			CurrentNode = CurrentNode->LeftChild;
		}

		CurrentNode = TopStack(Stack);
		cout << " " << CurrentNode->value << "-> ";
		pop_Stack(Stack);
		CurrentNode = CurrentNode->RightChild;
	}

	//cout << "<null>" << endl;
	destroyStack(Stack);
}

后序遍历

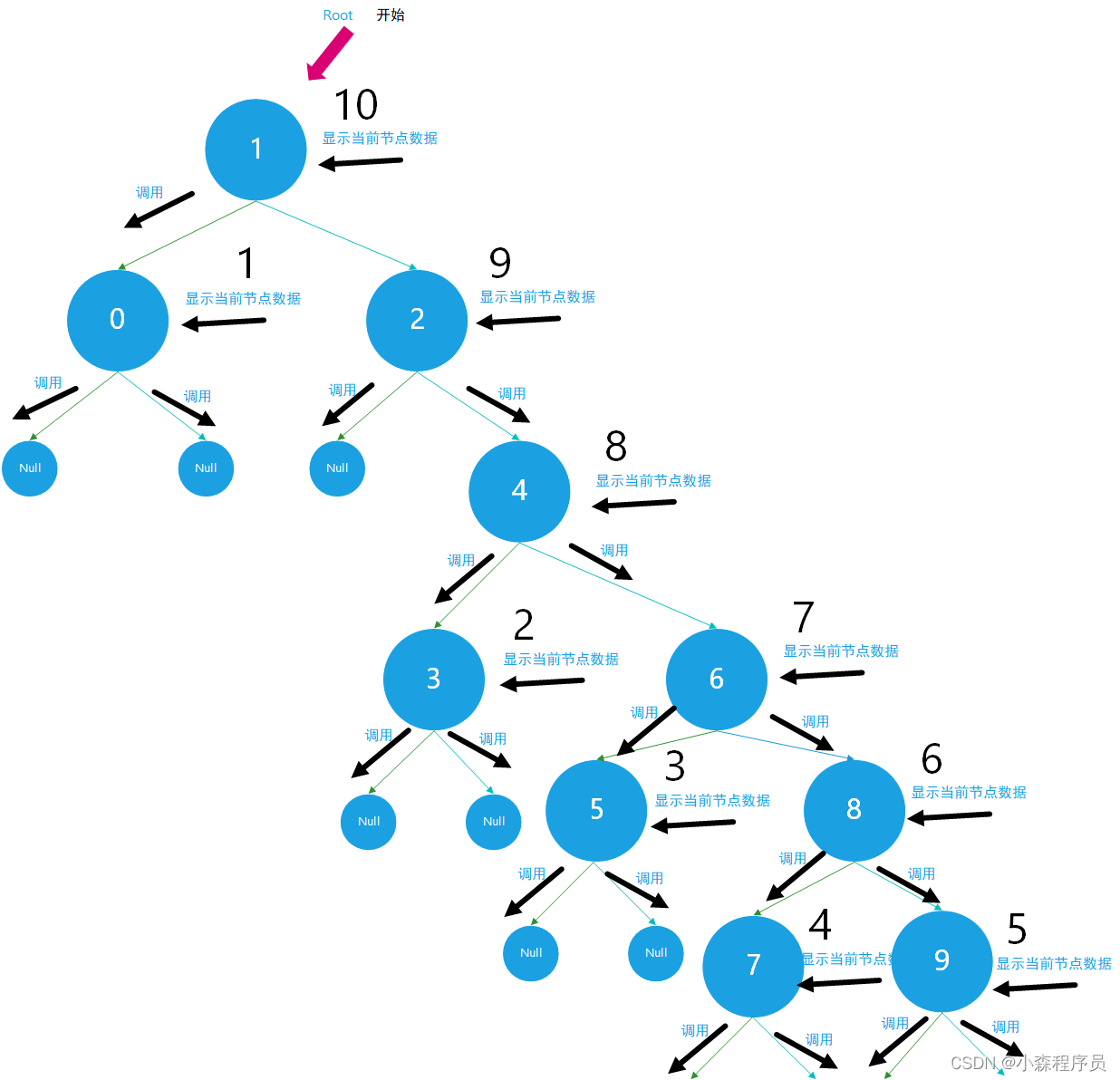
在这里插入图片描述

//非递归后序遍历
void  LastOrderNonRecursiveTraversal(TreeNode*& Root) {

	SeqStack Stack;
	initStack(Stack);
	auto CurrentNode = Root;
	decltype(CurrentNode) leafNode = nullptr;
	bool  isleafNode;
	push_Stack(Stack, CurrentNode);

	while (!emptyStack(Stack)) {


		CurrentNode = TopStack(Stack);

		isleafNode = (!CurrentNode->LeftChild && !CurrentNode->RightChild) || (leafNode != nullptr && (leafNode == CurrentNode->LeftChild || leafNode == CurrentNode->RightChild));
		if (isleafNode) {

			pop_Stack(Stack);
			leafNode = CurrentNode;
			cout << " " << CurrentNode->value << "-> ";
		}
		else {
			
			if (CurrentNode->RightChild) {
				push_Stack(Stack, CurrentNode->RightChild);
			}

			if (CurrentNode->LeftChild) {
				push_Stack(Stack, CurrentNode->LeftChild);
			}
		}
	}
	//cout << "<null>" << endl;
	destroyStack(Stack);
}

层序遍历

一层一层的遍历 直到 没有为止 相当于先序遍历

void LevelOrderTraversal(BinarySearchTree& tree) {

	cout << "<层序遍历> :";
	SeqQueue Queue;
	initQueue(Queue);
	auto CurrentNode = tree.Root;
	push_Queue(Queue, CurrentNode);
	while (!emptyQueue(Queue)) {

		CurrentNode = Queue_front(Queue);
		cout << CurrentNode->value << "-> ";
		pop_Queue(Queue);

		if (CurrentNode->LeftChild) {
			push_Queue(Queue, CurrentNode->LeftChild);
		}
		if (CurrentNode->RightChild) {
			push_Queue(Queue, CurrentNode->RightChild);
		}
	}
	cout << "<null>" << endl;
	destroyQueue(Queue);

}

销毁 二叉搜索树
根据只能用递归后序遍历来销毁 非递归不可以的

void DestroyBinarySearchTree(TreeNode* root) {
	if (root) {

		if (!root->LeftChild && !root->RightChild) {
			delete root;
		}
		else {
			if (root->LeftChild) {
				DestroyBinarySearchTree(root->LeftChild);
			}
			if (root->RightChild) {
				DestroyBinarySearchTree(root->RightChild);
			}
		}
	}
}


void DestroyBinarySearchTree(BinarySearchTree& tree) {

	DestroyBinarySearchTree(tree.Root);
	tree = {};
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/71568.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

用electron+vue+ts开发桌面应用

用electron+vue+ts开发桌面应用

1.搭建项目 npm create vitelatest安装electron插件 npm install electron -D npm install vite-plugin-electron -D这里安装插件会包如下错&#xff1a; 在终端执行&#xff1a; npm config set electron_mirror https://npm.taobao.org/mirrors/electron/配置参数 在vite…
阅读更多...
程序的翻译环境【编译链接的过程】【详解】

程序的翻译环境【编译链接的过程】【详解】

本期介绍&#x1f356; 主要介绍&#xff1a;代码是如何一步步的转化成可执行城西的&#xff0c;详细介绍了编译和链接的过程&#xff0c;特别是在编译还可分为预编译、编译、汇编三个阶段&#xff0c;介绍每个阶段分别干什么。&#x1f440;。 文章目录一、概述&#x1f356;二…
阅读更多...
手写一个简单的mybatis

手写一个简单的mybatis

1.写个简单的mybatis 今天写个简单版V1.0版本的mybatis&#xff0c;可以其实就是在jdbc的基础上一步步去优化的&#xff0c;网上各种帖子都是照着源码写&#xff0c;各种抄袭&#xff0c;没有自己的一点想法&#xff0c;写代码前要先思考&#xff0c;如果是你&#xff0c;你该…
阅读更多...
【数据库数据恢复】MS SQL数据库提示“附加数据库错误 823”怎么恢复数据？

【数据库数据恢复】MS SQL数据库提示“附加数据库错误 823”怎么恢复数据？

MS SQL Server是微软公司研发的数据库管理系统&#xff0c;SQL Server是一个可扩展的、高性能的、与WindowsNT有机结合的&#xff0c;为分布式客户机/服务器所设计的数据库管理系统&#xff0c;提供基于事务的企业级信息管理系统方案。 SQL Server数据库故障情况&分析&…
阅读更多...
RCNN学习笔记-MobileNet

RCNN学习笔记-MobileNet

Abstract 我们提出了一类叫做MobileNets的高效模型用于移动和嵌入式视觉应用。MobileNets基于一种简化的架构&#xff0c;该架构使用深度方向可分离卷积来构建轻量级深度神经网络。我们引入了两个简单的全局超参数&#xff0c;可以有效地在延迟和准确性之间进行权衡。这些超参…
阅读更多...
套用bi模板，轻松搞定各类数据分析报表

套用bi模板，轻松搞定各类数据分析报表

bi模板是什么?是一个个提前预设的报表设计&#xff0c;套用后立即生效&#xff0c;轻轻松松搞定bi数据可视化分析报表。bi模板都有哪些类型&#xff1f;怎么套用&#xff1f;以奥威bi数据可视化软件为例&#xff0c;聊聊bi模板的种类和下载使用。 bi模板有哪些&#xff1f; …
阅读更多...
Web Component入门

Web Component入门

本文作者为奇舞团前端开发工程师引言前端开发者&#xff0c;现在在进行项目的开发时&#xff0c;一般很少使用原生的js代码&#xff0c;往往都会依靠Vue&#xff0c;React等框架进行开发&#xff0c;而不同的框架都有自己不同的开发规则&#xff0c;但是目前所使用的主流框架&a…
阅读更多...
关于小程序swiper图片不能撑满解决方案

关于小程序swiper图片不能撑满解决方案

问题描述 最近在写小程序的时候使用了swiper组件&#xff0c;但是发现一个很奇怪的现象&#xff0c;如果给image组件设置mode“widthFix”的话&#xff0c;那么图片的高度是不够撑满swiper-item的这样就会导致swiper的指示器往下偏移&#xff08;其实没有偏移&#xff0c;只是…
阅读更多...
代码随想录刷题Day58 | 739. 每日温度 | 496. 下一个更大元素 I

代码随想录刷题Day58 | 739. 每日温度 | 496. 下一个更大元素 I

代码随想录刷题Day58 | 739. 每日温度 | 496. 下一个更大元素 I 739. 每日温度 题目&#xff1a; 给定一个整数数组 temperatures &#xff0c;表示每天的温度&#xff0c;返回一个数组 answer &#xff0c;其中 answer[i] 是指对于第 i 天&#xff0c;下一个更高温度出现在…
阅读更多...
剑指Offer51——数组中的逆序对

剑指Offer51——数组中的逆序对

摘要 剑指 Offer 51. 数组中的逆序对 一、暴力的方法 1.1 暴力的解析 使用两层 for 循环枚举所有的数对&#xff0c;逐一判断是否构成逆序关系。 1.2 复杂度分析 时间复杂度&#xff1a;O(N^2)&#xff0c;这里N是数组的长度&#xff1b;空间复杂度&#xff1a;O(1)。 1…
阅读更多...
【芯片应用】PA93

【芯片应用】PA93

文章目录一、简介二、原理1、外部连接&#xff08;1&#xff09;相位补偿&#xff08;2&#xff09;限流电阻一、简介 性质&#xff1a;高压运算放大器 厂商&#xff1a;美国 APEX Microtechnology公司 供电电压&#xff1a;Vs to -Vs&#xff1a;最高400V&#xff0c;即200V …
阅读更多...
【web课程设计】HTML+CSS仿QQ音乐网站

【web课程设计】HTML+CSS仿QQ音乐网站

&#x1f389;精彩专栏推荐 &#x1f4ad;文末获取联系 ✍️ 作者简介: 一个热爱把逻辑思维转变为代码的技术博主 &#x1f482; 作者主页: 【主页——&#x1f680;获取更多优质源码】 &#x1f393; web前端期末大作业&#xff1a; 【&#x1f4da;毕设项目精品实战案例 (10…
阅读更多...
【Windows基础】NTFS文件系统

【Windows基础】NTFS文件系统

NTFS文件系统 windows上的文件系统 早期Windows上使用&#xff1a;FAT16或FAT32&#xff08;Windows98&#xff09;目前Windows操作系统基本使用的是NTFS文件系统ReFS文件系统 ReFS&#xff08;Resilient File System&#xff0c;复原文件系统&#xff09;是在 Windows Serve…
阅读更多...
万众期待的Dyson Zone空气净化耳机确认将于中国首发，戴森重新定义“好声音”

万众期待的Dyson Zone空气净化耳机确认将于中国首发，戴森重新定义“好声音”

同享纯净音质与洁净空气&#xff0c;Dyson Zone™ 空气净化耳机确认将在中国开启全球首发 中国&#xff0c; 2022年12月8日 – 今日&#xff0c;戴森首次公开了Dyson Zone™ 空气净化耳机的详细技术参数&#xff0c;该产品已确认将在中国开启全球首发&#xff0c;并在戴森指定…
阅读更多...
玩好.NET高级调试，你也要会写点汇编

玩好.NET高级调试，你也要会写点汇编

一&#xff1a;背景 1. 简介 .NET 高级调试要想玩的好&#xff0c;看懂汇编是基本功&#xff0c;但看懂汇编和能写点汇编又完全是两回事&#xff0c;所以有时候看的多&#xff0c;总手痒痒想写一点&#xff0c;在 Windows 平台上搭建汇编环境不是那么容易&#xff0c;大多还是…
阅读更多...
[附源码]Python计算机毕业设计SSM佳音大学志愿填报系统（程序+LW)

[附源码]Python计算机毕业设计SSM佳音大学志愿填报系统（程序+LW)

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
Mybatis日志配置(slf4j、log4j、log4j2)

Mybatis日志配置(slf4j、log4j、log4j2)

文章目录1. Mybatis日志1.1 日志实现原理1.2 日志实现方式2. SLF4J2.1 slf4j日志级别2.2 日志门面与日志实现2.3 日志门面与日志依赖配置3. LOG4J3.1 日志级别3.2 log4j重要组件3.3 mybatis日志配置log4j3. LOG4J23.1 mybatis配置log4j23.2 log4j2配置文件1. Mybatis日志 1.1 …
阅读更多...
elasticsearch集群数据索引迁移自动化脚本

elasticsearch集群数据索引迁移自动化脚本

日常维护elasticsearch集群会出现新老集群数据迁移，这里使用的是snapshot api是Elasticsearch用于对数据进行备份和恢复的一组api接口，可以通过snapshot api进行跨集群的数据迁移，原理就是从源ES集群创建数据快照，然后在目标ES集群中进行恢复。 1、新老集群修改集群配置文…
阅读更多...
潦草手写体也能轻松识别，快速提取文字不用愁

潦草手写体也能轻松识别，快速提取文字不用愁

基于文本识别&#xff08;OCR&#xff09;技术的成熟与应用&#xff0c;日常生活中的大部分“印刷体识别”需求都能被满足&#xff0c;替代了人工信息录入与检测等操作&#xff0c;大大降低输入成本。 而对于复杂的手写体识别需求&#xff0c;业界识别质量却参差不齐。大部分手…
阅读更多...
【Linux】进程优先级进程切换

【Linux】进程优先级进程切换

索引➡️进程优先级1.什么叫做优先级2.为什么会存在优先级3.看看Linux怎么做的4.查看进程优先级的命令&#x1f60a;进程的一些特性➡️进程切换➡️进程优先级 1.什么叫做优先级 优先级和权限有些区别&#xff0c;权限决定能还是不能&#xff0c;优先级的前提是能&#xff0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023