摘要

剑指 Offer 51. 数组中的逆序对

一、暴力的方法

1.1 暴力的解析

使用两层 for 循环枚举所有的数对，逐一判断是否构成逆序关系。

1.2 复杂度分析

时间复杂度：O(N^2)，这里N是数组的长度；
空间复杂度：O(1)。

1.3 code 示例

/**
 * @description 采用的暴力的方式 这样的时间将超出限制
  * @param: nums
 * @date: 2022/12/8 8:59
 * @return: int
 * @author: xjl
*/
public int reversePairs(int[] nums) {
    int count=0;
    for (int i=0;i<nums.length;i++){
        for (int j=i+1;j<nums.length;j++){
            if (nums[j]<nums[i]){
                count++;
            }
        }
    }
    return count;
}

二、分治思想（借助归并排序统计逆序数）

2.1 分治思想解析

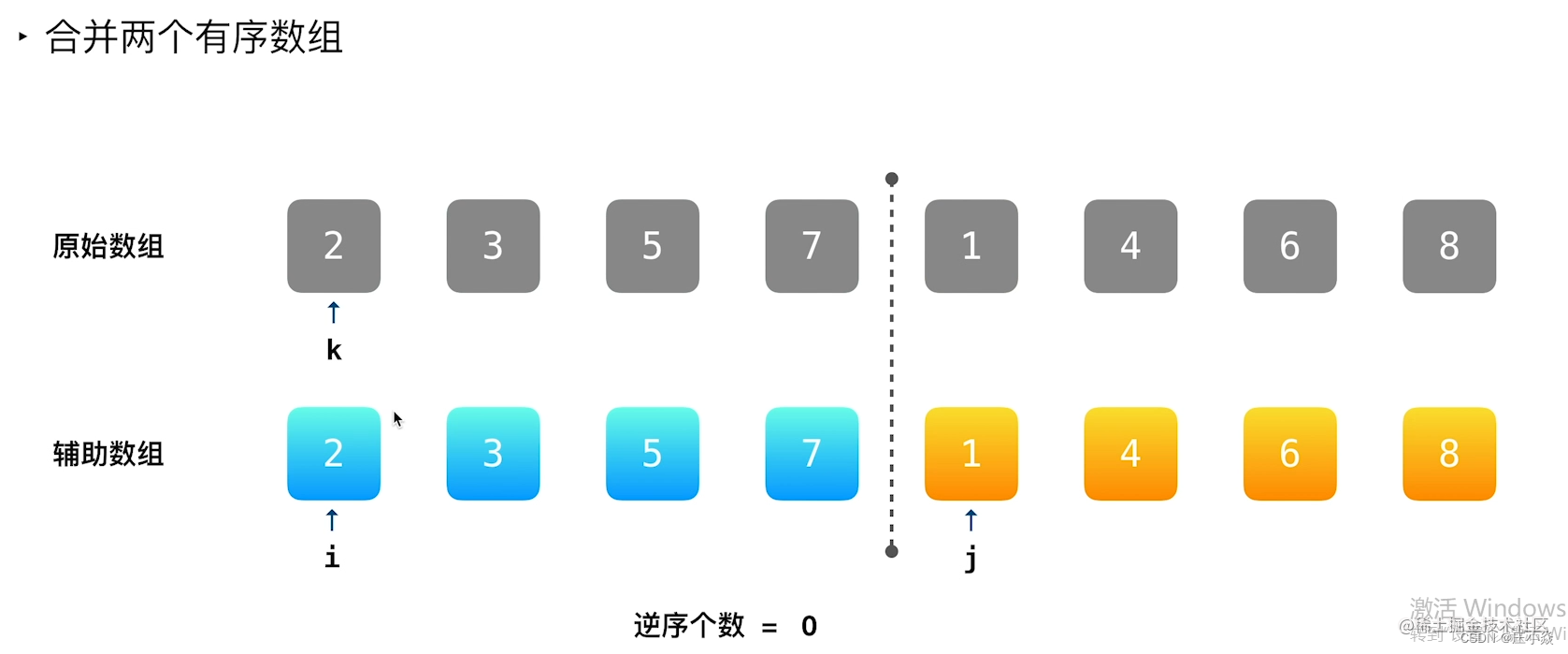
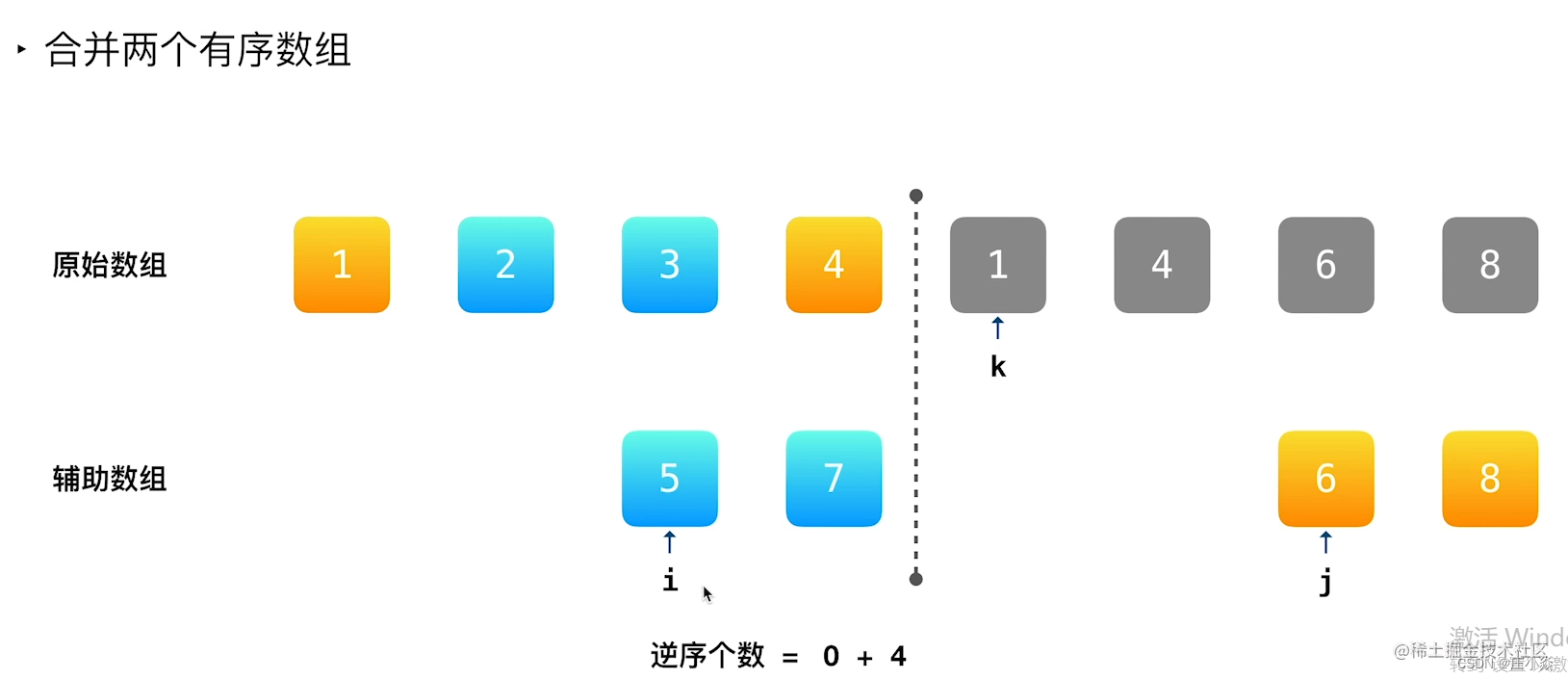
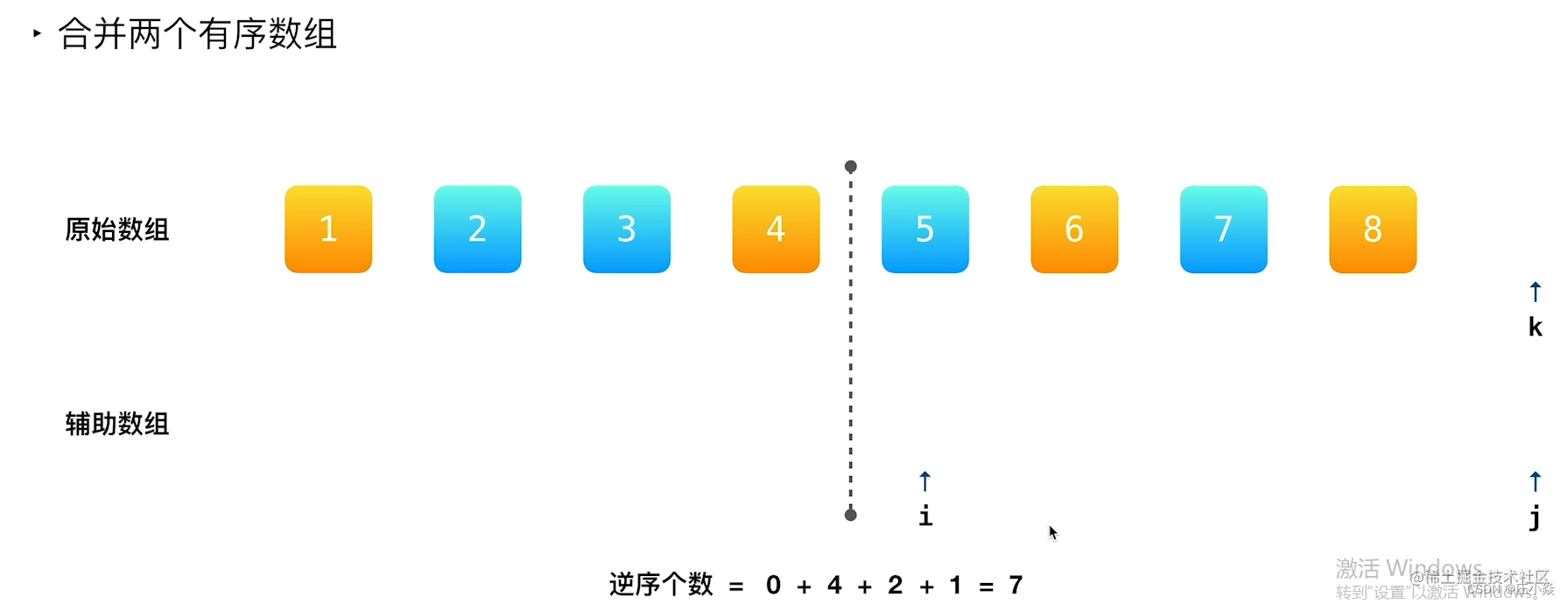
说明：理解这个算法需要对归并排序比较熟悉。掌握怎么样编写递归函数，每一次都一分为二拆分数组的子区间，然后在方法栈弹出的时候，一步一步合并两个有序数组，最后完成排序工作。而计算逆序数就发生在排序的过程中，利用了「排序」以后数组的有序性。

利用「归并排序」计算逆序对，是非常经典的做法；
关键在于「合并两个有序数组」的步骤，利用数组的部分有序性，一下子计算出一个数之前或者之后元素的逆序的个数；
前面「分」的时候什么都不做，「合」的过程中计算「逆序对」的个数；
排序的工作是必要的，正是因为「排序」才能在下一轮利用顺序关系加快逆序数的计算，也能避免重复计算；
代代码实现上，只需要在「归并排序」代码的基础上，加上「逆序对」个数的计算，计算公式需要自己在草稿纸上推导。

思想是「分治算法」，所有的「逆序对」来源于 3 个部分：

左边区间的逆序对；
右边区间的逆序对；
横跨两个区间的逆序对。

请添加图片描述

2.2 复杂度分析

时间复杂度：O(nlog(n))，这里N是数组的长度；
空间复杂度：O(n)。需要一个临时的数组。

2.3 code 示例

/**
 * @description 采用阶段性的排序的思想来实现数据的由于 进而可以计算当前的逆序数的个数
 * @param: nums
 * @date: 2022/12/8 10:10
 * @return: int
 * @author: xjl
 */
public int reversePairs2(int[] nums) {
    int len = nums.length;
    if (len < 2) {
        return 0;
    }
    // 拷贝原始数组
    int[] copy = Arrays.copyOf(nums, len);
    int[] temp = new int[len];
    return calculate(copy, 0, len - 1, temp);
}

/**
 * @description 计算nums[left……right] 计算逆序对的个数进行排序
 * @param: nums
 * @param: left
 * @param: right
 * @param: temp
 * @date: 2022/12/8 10:19
 * @return: int
 * @author: xjl
 */
private int calculate(int[] nums, int left, int right, int[] temp) {
    // 表示不能在分解了
    if (left == right) {
        return 0;
    }
    // 计算中间的值
    int mid = (left + right) >> 1;
    int leftcount = calculate(nums, left, mid, temp);
    int rightcount = calculate(nums, mid + 1, right, temp);
    // 合并后的结果
    int mergecount = mergeCount(nums, left, mid, right, temp);
    return leftcount + rightcount + mergecount;
}

/**
 * @description nums[left, mid]----nums[mid+1,right]是有序
 * @param: nums
 * @param: left
 * @param: rightcount
 * @param: temp
 * @date: 2022/12/8 10:24
 * @return: int
 * @author: xjl
 */
private int mergeCount(int[] nums, int left, int mid, int right, int[] temp) {
    for (int i = left; i <= right; i++) {
        temp[i] = nums[i];
    }
    int i = left;
    int j = mid + 1;
    int count = 0;
    // 三指针来讲数据重新的设置回原来的数组中 就是归并排序的思路
    for (int k = left; k <= right; k++) {
        if (i == mid + 1) {
            nums[k] = temp[j];
            j++;
        } else if (j == right + 1) {
            nums[k] = temp[i];
            i++;
        } else if (temp[i] <= temp[j]) {
            nums[k] = temp[i];
            i++;
        } else {
            // 只有在 temp[j]小于左边的最小值的时候 才去计算 这个时候的逆序数对的个数才是: mid-i+1;
            nums[k] = temp[j];
            j++;
            count += (mid - i) + 1;
        }
    }
    return count;
}