第九章在CDGA分值占比较少,CDGP不考核,主要考点包括:定义、目标、原则、活动、工具、度量指标等基本概念、记住精心管理档案特点、GARP原则等。因此本章建议不需要花大量时间研究,熟悉历史真题,聚焦关键考点即可!
CDGA考题分布:2题,共2分
CDGP考题分布:不考核
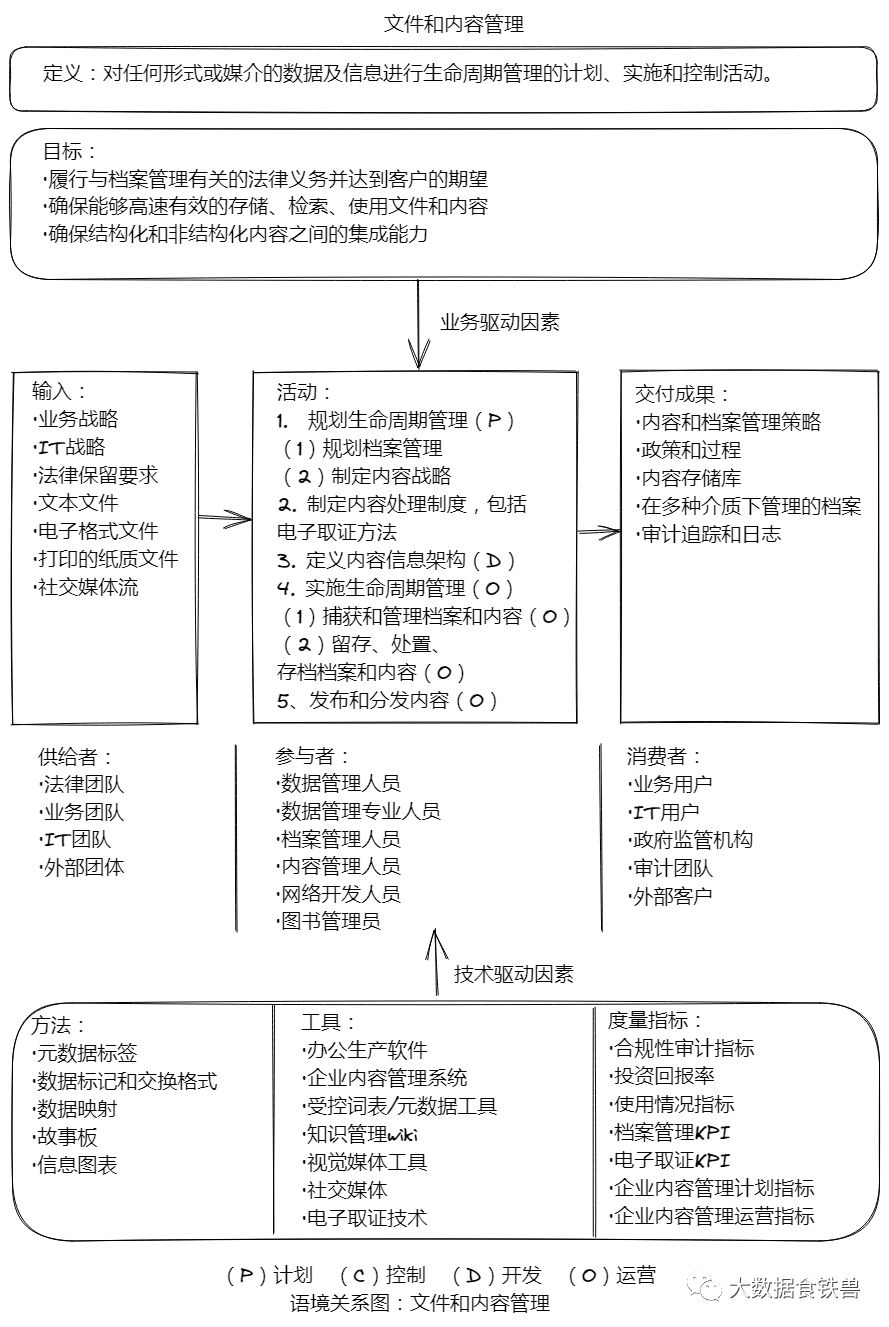
加gzh“大数据食铁兽”,回复“知识点”,获取《DMBOK知识梳理for CDGA/CDGP》常考知识点(第九章 文件和内容管理)
历史真题:真题答案请查看文末
1、请从下列选项中选择能够最大范围管理非结构化数据的系统。
A. 网盘/文档系统
B.档案系统
c.影像系统。
D. ECM企业内容管理系统
2、文件和内容管理的主要业务驱动因素不包括
A.法规遵从性
B.诉讼应诉和电子取证请求的能力
C.业务连续性要求
D.保密性要求
3、根据DMBOK2,实施文件和内容管理最佳实践的目标不包括以下哪个选项
A.确保能够高速有效地的采集和使用非结构化的数据和信息
B.确保结构化和非结构化数据之间的整合能力。
c.实现非结构化数据的统一管理,提升安全性。
D.遵守法律义务并达到客户预期

真题答案:1、D 2、D 3、C