在这个项目中，我们将学习如何使用卷积变分自动编码器 (CVAE) 来处理和重建 3D 湍流数据。

我们使用计算流体动力学 (CFD) 方法生成 3D 湍流立方体，每个 3D 立方体沿着三个速度分量携带物理信息（与图像数据类似，被视为单独的通道）。

推荐：用 NSDT设计器 快速搭建可编程3D场景。

作为 3D CFD 数据预处理的一部分，我们编写了一个自定义 pytorch 数据加载器，用于对数据集执行标准化和批处理操作。

CVAE 对预处理后的数据实施 3D 卷积 (3DConvs) 来执行重建。

通过微调超参数和操纵我们的模型架构，我们在 3D 重建方面取得了显着的进步。

可以在这个 Github 存储库中找到项目代码。

1、数据说明

我们的数据集是使用 CFD 模拟方法生成的，它包含从供暖通风和空调 (HVAC) 管道中提取的立方体。

每个立方体代表特定时间携带物理信息的湍流的三维时间快照。 从模拟中提取的信息基于两个流动分量：速度场 U 和静压 p。 U 场 (x, y, z) 和标量 p 基于流的方向（立方体的法线方向）。

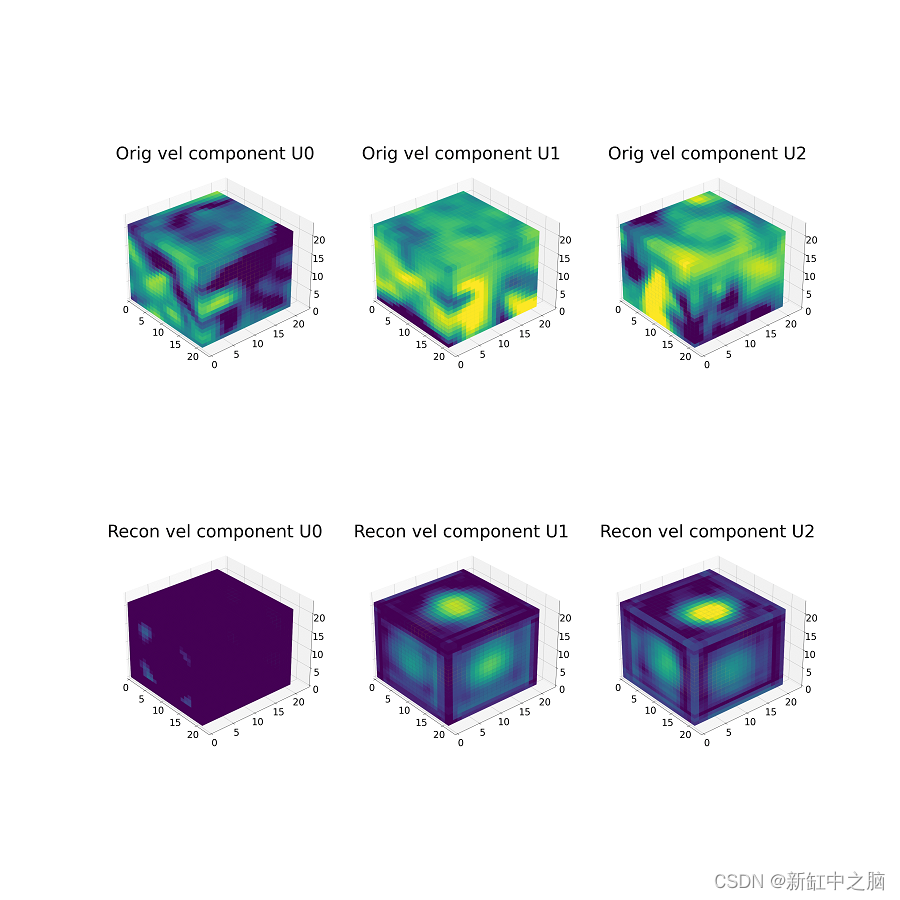
我们使用体素将 3D 立方体表示为尺寸为 21 × 21 × 21 x 100（x_coord、y_coord、z_coord、timestep）的数组。 下图显示了一个立方体数据样本，我们使用热图可视化每个速度分量。

总的来说，该数据集由 96 个模拟组成，每个模拟有 100 个时间步长，总共 9600 个立方体（对于每个速度分量）。

注意：由于保密限制，我们不会公开我们的数据，你可以使用脚本并将其改编为自己的 3D 数据。

2、数据预处理

下面的脚本显示了为预处理 3D 数据而编写的自定义 pytorch 数据加载器。 以下是一些亮点：

• 立方体速度通道的加载和串联
• 数据标准化
• 数据缩放

请参阅存储库中的 dataloader.py 脚本以了解完整的实现。

3、模型架构

下图显示了已实现的 CVAE 架构。 在本例中，为了清晰起见，显示了 2DConv，但实现的架构使用 3DConv。

CVAE 由编码器网络（上部）、变分层（mu 和 sigma）（中右部分）和解码器网络（底部）组成。

编码器对输入立方体执行下采样操作，解码器对它们进行上采样以恢复原始形状。 变分层尝试学习数据集的分布，该层稍后可用于生成。

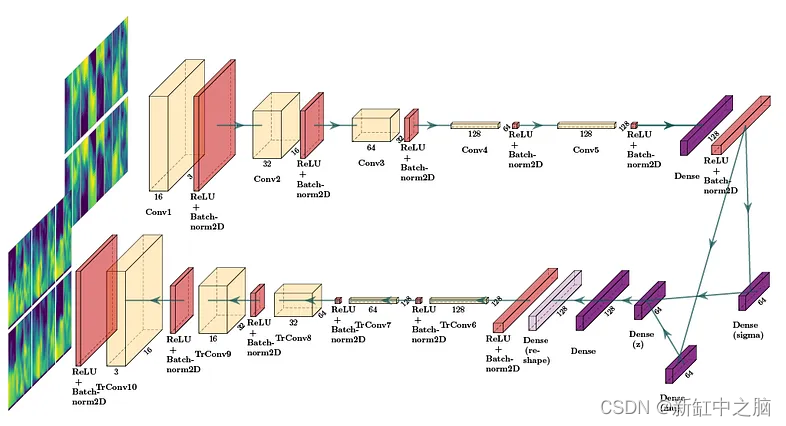
编码器网络由四个 3D 卷积层组成，每层的卷积滤波器数量是前一层的两倍（分别为 32、64、128 和 256），这使得模型能够学习更复杂的流特征。

密集层用于组合从最后一个编码器层获得的所有特征图，该层连接到计算后验流数据分布的参数（mu和sigma，这些参数使用重新定义概率分布）的变分层。 -[1]中描述的参数化技巧。这种概率分布允许我们从中采样，以生成尺寸为 8 × 8 x 8 的合成 3D 立方体。

解码器网络采用潜在向量并应用四个 3D 转置卷积层来恢复（重建）原始数据维度，每一层的卷积滤波器数量是前一层的一半（分别为 256、128、64 和 32）。

CVAE 使用两个损失函数进行训练：用于重建的均方误差 (MSE) 和用于潜在空间正则化的 Kullback-Leibler 散度 (KLB)。

我们将[2]中提出的架构和[3]中的超参数作为基线架构。

下面的脚本显示了 pytorch 中的一个示例，其中编码器和解码器都是使用 3D 卷积层 (Conv3d) 定义的：

self.encoder = nn.Sequential(
            nn.Conv3d(in_channels=image_channels, out_channels=16, kernel_size=4, stride=1, padding=0),
            nn.BatchNorm3d(num_features=16),
            nn.ReLU(),
            nn.Conv3d(in_channels=16, out_channels=32, kernel_size=4, stride=1, padding=0),
            nn.BatchNorm3d(num_features=32),
            nn.ReLU(),
            nn.Conv3d(in_channels=32, out_channels=64, kernel_size=4, stride=1, padding=0),
            nn.BatchNorm3d(num_features=64),
            nn.ReLU(),
            nn.Conv3d(in_channels=64, out_channels=128, kernel_size=4, stride=1, padding=0),
            nn.BatchNorm3d(num_features=128),
            nn.ReLU(),
            nn.Conv3d(in_channels=128, out_channels=128, kernel_size=4, stride=1, padding=0),
            nn.BatchNorm3d(num_features=128),
            nn.ReLU(),
            Flatten()
        )

self.decoder = nn.Sequential(
            UnFlatten(),
            nn.BatchNorm3d(num_features=128),
            nn.ReLU(),
            nn.ConvTranspose3d(in_channels=128, out_channels=128, kernel_size=4, stride=1, padding=0),
            nn.BatchNorm3d(num_features=128),
            nn.ReLU(),
            nn.ConvTranspose3d(in_channels=128, out_channels=64, kernel_size=4, stride=1, padding=0),
            nn.BatchNorm3d(num_features=64),
            nn.ReLU(),
            nn.ConvTranspose3d(in_channels=64, out_channels=32, kernel_size=4, stride=1, padding=0),
            nn.BatchNorm3d(num_features=32),
            nn.ReLU(),
            nn.ConvTranspose3d(in_channels=32, out_channels=16, kernel_size=4, stride=1, padding=0),
            nn.BatchNorm3d(num_features=16),
            nn.ReLU(),
            nn.ConvTranspose3d(in_channels=16, out_channels=image_channels, kernel_size=4, stride=1, padding=0), # dimensions should be as original
            nn.BatchNorm3d(num_features=3))

4、设置环境

克隆此存储库：

git clone git@github.com:agrija9/Convolutional-VAE-for-3D-Turbulence-Data

建议使用虚拟环境来运行本项目：

• 可以安装Anaconda并在系统中创建环境
• 可以使用 pip venv 创建环境

在 pip/conda 环境中安装以下依赖项：

• NumPy (>= 1.19.2)
• Matplotlib (>= 3.3.2)
• PyTorch (>= 1.7.0)
• Torchvision (>= 0.8.1)
• scikit-learn (>= 0.23.2)
• tqdm
• tensorboardX
• torchsummary
• PIL
• collections

5、模型训练

要训练模型，请打开终端，激活 pip/conda 环境并输入：

cd /path-to-repo/Convolutional-VAE-for-3D-Turbulence-Data
python main.py --test_every_epochs 3 --batch_size 32 --epochs 40 --h_dim 128 --z_dim 64

以下是一些可以修改的超参数来训练模型

• –batch_size 每个补丁要处理的立方体数量
• –epochs 训练纪元数
• –h_dim 隐藏密集层的维度（连接到变分层）
• –z_dim 潜在空间维度

main.py 脚本调用模型并根据 3D CFD 数据对其进行训练。 使用 NVIDIA Tesla V100 GPU 训练 100 个 epoch 大约需要 2 小时。 在本例中，模型训练了 170 个 epoch。

请注意，在训练 3DConvs 模型时，与 2DConvs 模型相比，学习参数的数量呈指数级增长，因此，3D 数据的训练时间要长得多。

6、模型输出

训练完pytorch模型后，会生成一个包含训练后的权重的文件checkpoint.pkl。

在训练过程中，每隔 n 个时期根据测试数据对模型进行评估，脚本将重建的立方体与原始立方体进行比较，并将它们保存为图像。 此外，损失值被记录并放置在运行文件夹中，可以通过输入以下内容使用张量板可视化损失曲线：

cd /path-to-repo/Convolutional-VAE-for-3D-Turbulence-Data
tensorboard --logdir=runs/

如果没有创建，文件夹runs/会自动生成。

7、3D 重建结果

下图中，我们展示了同一立方体样本每 n 个 epoch 的重建结果。

顶行包含原始立方体样本（对于每个速度通道）。 底行包含每 n 个时期的重建输出。

对于这个例子，我们展示了从 0 到 355 个时期的重建，间隔为 15 个时期。 请注意作为历元函数的重建的改进。

---

原文链接：3D VAE神经网络实战 — BimAnt