有了前面两节的背景知识，我们来构造一个目标检测模型，就是来自Wei Liu大神之作的SSD了，有兴趣的可以查阅论文：SSD: Single Shot MultiBox Detector

计算机视觉之目标检测(object detection)《1》https://blog.csdn.net/weixin_41896770/article/details/128062645
计算机视觉之目标检测训练数据集（皮卡丘）《2》https://blog.csdn.net/weixin_41896770/article/details/128147117

一般我都会先看完原论文，里面除了讲解模型以及和其他模型的对比，还有一些开放式的讨论，可以留给自己思考。
SSD由于它简单且快速，得到了广泛的应用，该模型的一些设计思想和实现细节常适用于其他目标检测模型。SSD单发多框检测模型，是一个多尺度的目标检测模型，基于基础网络块和各个多尺度特征块生成不同数量和不同大小的锚框，并通过预测锚框的类别和偏移量检测不同大小的目标。

本人还是画个图，让大家直观感受下这个模型的层级构造，每层都会输出锚框（且数量和大小都不一样），然后依据锚框的类别与偏移量(即预测边界框)来检测不同大小的目标。这也是SSD属于多尺度的目标检测模型的原因。

类别预测层与预测边界框

从图中我们可以看到，每个层都输出不同数量和不同大小的锚框，并预测锚框的类别和偏移量(预测边界框)来检测不同大小的目标，我们先实现类别预测与预测边界框的方法：

import d2lzh as d2l
from mxnet import gluon, image, nd, init, contrib, autograd
from mxnet.gluon import loss as gloss, nn
import time


def cls_predictor(num_anchors, num_classes):
    '''
    类别预测层

    参数
    ------
    通道数：num_anchors*(num_classes+1)
        其中类别数需要加一个背景
    卷积核大小：3，填充：1
        可以保持输出的高宽不变
    '''
    return nn.Conv2D(num_anchors*(num_classes+1), kernel_size=3, padding=1)

def bbox_predictor(num_anchors):
    '''
    边界框预测层

    参数
    -----
    通道数：num_anchors*4
        为每个锚框预测4个偏移量
    '''
    return nn.Conv2D(num_anchors*4,kernel_size=3,padding=1)

def forward(x,block):
    block.initialize()
    return block(x)
Y1=forward(nd.zeros((2,8,20,20)),cls_predictor(5,10))
Y2=forward(nd.zeros((2,16,10,10)),cls_predictor(3,10))
print(Y1.shape,Y2.shape)#(2, 55, 20, 20) (2, 33, 10, 10)

可以看出计算出的输出形状中的通道数：55=5*(10+1),33=3*(10+1)符合我们的预期，留给大家一个思考，为什么这里出现通道数或者说要转换到通道数？
每个尺度上特征图的形状或以同一单元为中心生成的锚框数量可能不同，所以不同尺度的预测输出的形状就可能不同。

形状转换连结

上面提到的预测的形状可能不同，又如何将他们的多尺度预测输出都连结起来呢？这里需要做一个形状的变换，我们先来看个小示例：

def flatten_pred(pred):
    return pred.transpose((0,2,3,1)).flatten()
def concat_preds(preds):
    return nd.concat(*[flatten_pred(p) for p in preds],dim=1)
print(flatten_pred(Y1).shape,flatten_pred(Y2).shape)#(2, 22000) (2, 3300)
print(concat_preds([Y1,Y2]).shape)#(2, 25300)

从结果也看出，虽然Y1,Y2的形状不同(批量大小一样)，但是通过flatten()转换之后，我们还是可以将这两个不同尺度的预测结果连结在一起(维度1上进行连结)。
注意与numpy里的区别，不要搞混淆了，在np里面是摊平成一维数组，比如：
nd中flatten_pred(Y1).shape返回的是形状为(2, 22000)的二维数组，如果是np的话，形状则为(44000,)的一维数组
附带说下那个*星号的用法，简单粗暴的理解就是剥掉最外面的一个中括号：

>>> print([i for i in [1,2,3,4]])
[1, 2, 3, 4]
>>> print(*[i for i in [1,2,3,4]])
1 2 3 4
>>> print([i for i in [[1,2,3,4],[5,6,7,8]]])
[[1, 2, 3, 4], [5, 6, 7, 8]]
>>> print(*[i for i in [[1,2,3,4],[5,6,7,8]]])
[1, 2, 3, 4] [5, 6, 7, 8]

SSD模型

然后我们来构造一个SSD的模型，我们回看上面的图来构造，设计基础网络块，用来从原始图像提取特征，这里构造一个小的基础网络，串联3个高宽减半块，以及将通道数翻倍。
先实现一个高宽减半块，这样的模块是为了最终让输出特征图中每个单元的感受野变得更广阔。

def down_sample_blk(num_channels):
    '''
    高宽减半块
        步幅为2的2x2的最大池化层将特征图的高宽减半
    串联两个卷积层和一个最大池化层
    '''
    blk = nn.Sequential()
    for _ in range(2):
        blk.add(nn.Conv2D(num_channels, kernel_size=3, padding=1),
                nn.BatchNorm(in_channels=num_channels), nn.Activation('relu'))
    blk.add(nn.MaxPool2D(pool_size=(2, 2), strides=2))
    return blk
print(forward(nd.zeros((2, 3, 20, 20)), down_sample_blk(10)).shape)# (2, 10, 10, 10)

def base_net():
    '''
    基础网络块
        串联3个高宽减半块，以及通道数翻倍
    '''
    blk = nn.Sequential()
    for n in [16, 32, 64]:
        blk.add(down_sample_blk(n))
    return blk

#print(forward(nd.zeros((2, 3, 256, 256)), base_net()).shape)  #(2, 64, 32, 32)

 然后对每个块做前向计算，一层：基础网络：二三四层：高宽减半块；五层：全局最大池化层

def get_blk(i):
    if i == 0:
        blk = base_net()
    elif i == 4:
        blk = nn.GlobalMaxPool2D()
    else:
        blk = down_sample_blk(128)
    return blk


def blk_forward(X, blk, size, ratio, cls_predictor, bbox_predictor):
    Y = blk(X)
    anchors = contrib.nd.MultiBoxPrior(Y, sizes=size, ratios=ratio)
    cls_preds = cls_predictor(Y)
    bbox_preds = bbox_predictor(Y)
    return (Y, anchors, cls_preds, bbox_preds)

sizes = [[0.2, 0.272], [0.37, 0.447], [0.54, 0.619], [0.71, 0.79], [0.88, 0.961]]
ratios = [[1, 2, 0.5]]*5
num_anchors = len(sizes[0])+len(ratios[0])-1


class TinySSD(nn.Block):
    def __init__(self, num_classes, **kwargs):
        super(TinySSD, self).__init__(**kwargs)
        self.num_classes = num_classes
        for i in range(5):
            setattr(self, 'blk_%d' % i, get_blk(i))
            setattr(self, 'cls_%d' %i, cls_predictor(num_anchors, num_classes))
            setattr(self, 'bbox_%d' % i, bbox_predictor(num_anchors))

    def forward(self, X):
        anchors, cls_preds, bbox_preds = [None]*5, [None]*5, [None]*5
        for i in range(5):
            X, anchors[i], cls_preds[i], bbox_preds[i] = blk_forward(X, getattr(self, 'blk_%d' % i), sizes[i], ratios[i],
                                                                     getattr(self, 'cls_%d' % i),
                                                                     getattr(self, 'bbox_%d' % i))
        return (nd.concat(*anchors, dim=1),
                concat_preds(cls_preds).reshape(0, -1, self.num_classes+1),
                concat_preds(bbox_preds))

net=TinySSD(num_classes=1)
net.initialize()
X=nd.zeros((32,3,256,256))
anchors,cls_preds,bbox_preds=net(X)
print("锚框：",anchors.shape)#锚框： (1, 5444, 4)
print("类别预测：",cls_preds.shape)#类别预测： (32, 5444, 2)
print("预测边界框：",bbox_preds.shape)#预测边界框： (32, 21776)

其中锚框数是5444个，是怎么得来的：一层输出的特征图形状是32x32，二层到四层是高宽减半，分别为16x16、8x8、4x4的宽高，第五层是全局池化层到1x1，由于是以特征图每个单元为中心生成4个锚框，所以每个图像在5个尺度下生成的锚框总数为(32x32+16x16+8x8+4x4+1)x4=5444

训练模型

同样使用前面用到的皮卡丘数据集，加载并初始化模型参数：

#加载皮卡丘数据集并初始化模型
batch_size=8#本人配置不行，批处理大小调小点
train_iter,_=d2l.load_data_pikachu(batch_size)
ctx,net=d2l.try_gpu(),TinySSD(num_classes=1)
net.initialize(init=init.Xavier(),ctx=ctx)
trainer=gluon.Trainer(net.collect_params(),'sgd',{'learning_rate':0.2,'wd':5e-4})

接下来定义损失函数，这里的损失函数和前面的训练模型的损失函数有点区别。
需要两个损失：一个是有关锚框类别的损失，另一个是有关正类锚框偏移量的损失。然后将两个损失相加就得到了最终损失函数。

#定义损失函数
cls_loss=gloss.SoftmaxCrossEntropyLoss()
bbox_loss=gloss.L1Loss()
def calc_loss(cls_preds,cls_labels,bbox_preds,bbox_labels,bbox_masks):
    cls=cls_loss(cls_preds,cls_labels)
    bbox=bbox_loss(bbox_preds*bbox_masks,bbox_labels*bbox_masks)
    return cls+bbox
#评价函数
def cls_eval(cls_preds,cls_labels):
    #类别预测结果放在最后一维，所以argmax需指定最后一维
    return (cls_preds.argmax(axis=-1)==cls_labels).sum().asscalar()
def bbox_eval(bbox_preds,bbox_labels,bbox_masks):
    return ((bbox_labels-bbox_preds)*bbox_masks).abs().sum().asscalar()

#训练模型
for epoch  in range(20):
    acc_sum,mae_sum,n,m=0.0,0.0,0,0
    train_iter.reset()
    start=time.time()
    for batch in train_iter:
        X=batch.data[0].as_in_context(ctx)
        Y=batch.label[0].as_in_context(ctx)
        with autograd.record():
            #生成多尺度锚框，为每个锚框预测类别和偏移量
            anchors,cls_preds,bbox_preds=net(X)
            bbox_labels,bbox_masks,cls_labels=contrib.nd.MultiBoxTarget(anchors,Y,cls_preds.transpose((0,2,1)))
            l=calc_loss(cls_preds,cls_labels,bbox_preds,bbox_labels,bbox_masks)
        l.backward()
        trainer.step(batch_size)
        acc_sum+=cls_eval(cls_preds,cls_labels)
        n+=cls_labels.size
        mae_sum+=bbox_eval(bbox_preds,bbox_labels,bbox_masks)
        m+=bbox_labels.size
    if(epoch+1)%5==0:
        print('迭代次数：%2d,类别损失误差：%.2e,正类锚框偏移量平均绝对误差：%.2e,耗时：%.1f秒'%(epoch+1,1-acc_sum/n,mae_sum/m,time.time()-start))
net.collect_params().save('ssd.params')

迭代次数： 5,类别损失误差：2.50e-03,正类锚框偏移量平均绝对误差：2.61e-03,耗时：17.4秒
迭代次数：10,类别损失误差：2.31e-03,正类锚框偏移量平均绝对误差：2.32e-03,耗时：17.4秒
迭代次数：15,类别损失误差：2.09e-03,正类锚框偏移量平均绝对误差：2.06e-03,耗时：17.4秒
迭代次数：20,类别损失误差：2.04e-03,正类锚框偏移量平均绝对误差：1.96e-03,耗时：17.4秒

相关知识，有兴趣可以查阅：Softmax回归模型的构建和实现（Fashion-MNIST图像分类）
另外掩码变量bbox_masks令负类锚框和填充锚框不参与损失的计算。

多尺度目标检测测试

现在我们来进入最后的预测阶段，将图像中我们感兴趣的目标检测出来。我们通过MultiBoxDetection函数根据锚框以及预测偏移量得到预测边界框，并通过非极大值抑制移除相似的预测边界框。最后我们将置信度不低于0.3的边界框筛选为最终输出用以展示。

img=image.imread('pikachu.png')#自己PS一张图
feature=image.imresize(img,256,256).astype('float32')
X=feature.transpose((2,0,1)).expand_dims(axis=0)#转换成卷积层需要的四维格式

net.collect_params().load('ssd.params')

def predict(X):
    anchors,cls_preds,bbox_preds=net(X.as_in_context(ctx))
    cls_probs=cls_preds.softmax().transpose((0,2,1))
    output=contrib.nd.MultiBoxDetection(cls_probs,bbox_preds,anchors)
    idx=[i for i,row in enumerate(output[0]) if row[0].asscalar()!=-1]
    return output[0,idx]

output=predict(X)

d2l.set_figsize((5,5))

def display(img,output,threshold):
    fig=d2l.plt.imshow(img.asnumpy())
    for row in output:
        score=row[1].asscalar()
        if score<threshold:
            continue
        h,w=img.shape[0:2]
        bbox=[row[2:6]*nd.array((w,h,w,h),ctx=row.context)]
        d2l.show_bboxes(fig.axes,bbox,'%.2f'%score,'w')

display(img,output,threshold=0.1)
d2l.plt.show()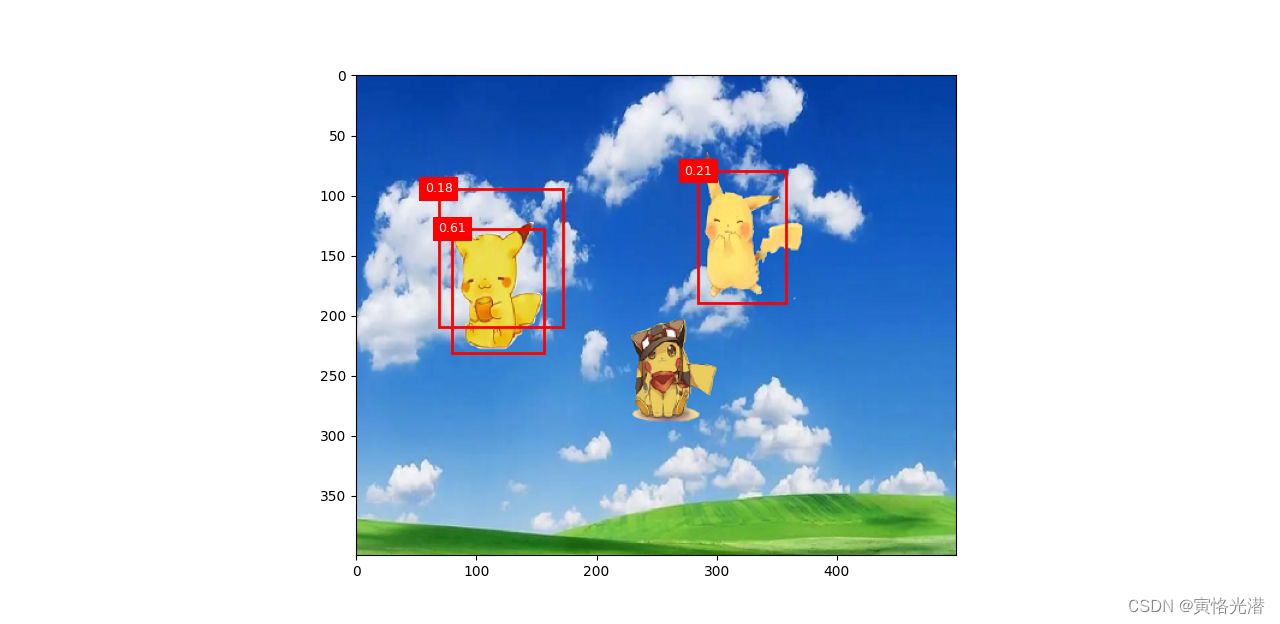

当然在做预测测试的时候最好训练一遍就将优化好的参数保存起来，不然每次都训练一次还是很耽误时间的，也没必要。

net.collect_params().save('ssd.params')

这样我们在进行输入预测之前就可以加载优化好的参数了。 

net.collect_params().load('ssd.params')

我将置信度调到了0.1，不然有时候还找不到^_^
从预测图来看，置信度不怎么准确，原因估计是皮卡丘的数据集比较小的关系，戴帽子的皮卡丘没有找到，当然也跟我的批处理大小调小了也有关系，大家硬件配置好的就调大点，有兴趣的可以自己试试，选择一张背景图然后上面放一些皮卡丘的图。