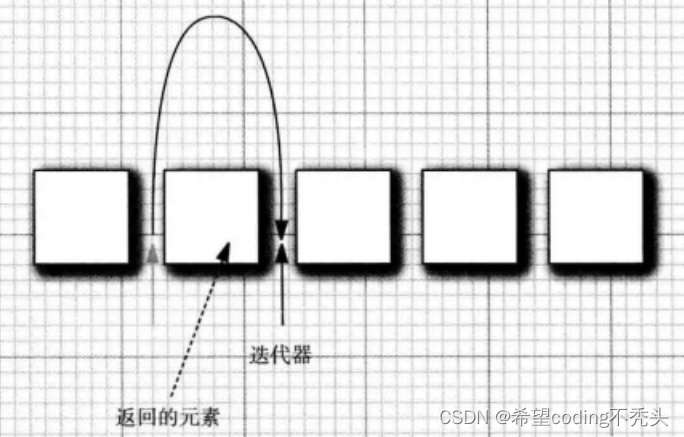
什么是分类
什么是聚类
引申一下有监督学习,半监督学习,无监督学习
区分有监督和无监督,就是看是否有监督(supervised)(这TM不是废话嘛!确实是废话),也就看输入数据是否有标签(label)。输入数据有标签,则为有监督学习(x,y),没标签则为无监督学习(x)。
举个栗子,在中学学习的时候,所有学习的终极目标就是考试,每次模考就是检测学习的一个过程,考的好与坏,都是有标准答案去判定的,这就是有监督学习。
但是走上社会了,没有分数和答案的制约了,学习不论好坏,不论方向,这就是无监督学习。
那么半监督呢?大学嘛,浪里个浪,大部分时间自由发挥,考前一周开始临时抱佛脚,直接开启super power模式,期末考过就行(60分万岁!!!)
聚类样本间的属性
聚类的常见算法
聚类算法分为三大类:
K-Means聚类
k-means聚类算法的分析流程:

层次聚类
自顶向下算法
Hierarchical K-means算法是“自顶向下”的层次聚类算法,用到了基于划分的聚类算法那K-means,算法思路如下:
1.首先,把原始数据集放到一个簇C,这个簇形成了层次结构的最顶层;
2.使用K-means算法把簇C划分成指定的K个子簇C_i,i = 1,2,…,k,形成一个新的层;
3.对于步骤2所生成的K个簇,递归使用K-means算法划分成更小的子簇,直到每个簇不能再划分(只包含一个数据对象)或者满足设定的终止条件。

Hierarchical K-means算法一个很大的问题是,一旦两个点在最开始被划分到了不同的簇,即使这两个点距离很近,在后面的过程中也不会被聚类到一起。

对于以上的例子,红色椭圆框中的对象聚类成一个簇可能是更优的聚类结果,但是由于橙色对象和绿色对象在第一次K-means就被划分到不同的簇,之后也不再可能被聚类到同一个簇。
你在脑海,你在心田,你在天边
嗯哼,网抑云时间结束
自底向上算法
Agglomerative Clustering算法
相比于Hierarchical K-means算法存在的问题,Agglomerative Clustering算法能够保证距离近的对象能够被聚类到一个簇中,该算法采用的“自底向上”聚类的思路。
算法思路,对于数据集D,D={x_1,x_2,…,x_n}:
1.将数据集中的每个对象生成一个簇,得到簇列表C,C={c_1,c_2,…,c_n} a) 每个簇只包含一个数据对象:c_i={x_i};
2.重复如下步骤,直到C中只有一个簇: a) 从C中的簇中找到两个“距离”最近的两个簇:min〖D(c_i,c_j)〗; b) 合并簇c_i和cj,形成新的簇c(i+j); c) 从C中删除簇c_i和cj,添加簇c(i+j)
簇间距离计算
在上面描述的算法中涉及到计算两个簇之间的距离,对于簇C_1和C_2,计算〖D(C_1,C〗_2),有以下几种计算方式:
单连锁(Single link)

两个簇之间最近的两个点的距离作为簇之间的距离,该方式的缺陷是受噪点影响大,容易产生长条状的簇。
全连锁(Complete link)
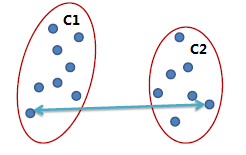
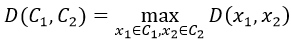
两个簇之间最远的两个点的距离作为簇之间的距离,采用该距离计算方式得到的聚类比较紧凑。
平均连锁(Average link)
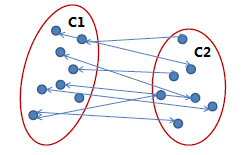

两个簇之间两两点之间距离的平均值,该方式可以有效地排除噪点的影响。
Agglomerative算法示例
对于如下数据:

- 将A到F六个点,分别生成6个簇;
找到当前簇中距离最短的两个点,这里我们使用单连锁的方式来计算距离,发现A点和B点距离最短,将A和B组成一个新的簇,此时簇列表中包含五个簇,分别是{A,B},{C},{D},{E},{F},如下图所示;

2 . 找到当前簇中距离最短的两个点,这里我们使用单连锁的方式来计算距离,发现A点和B点距离最短,将A和B组成一个新的簇,此时簇列表中包含五个簇,分别是{A,B},{C},{D},{E},{F},如下图所示;
3 . 重复步骤二、发现{C}和{D}的距离最短,连接之,然后是簇{C,D}和簇{E}距离最短,依次类推,直到最后只剩下一个簇,得到如下所示的示意图:

4 .此时原始数据的聚类关系是按照层次来组织的,选取一个簇间距离的阈值,可以得到一个聚类结果,比如在如下红色虚线的阈值下,数据被划分为两个簇:簇{A,B,C,D,E}和簇{F}

Agglomerative聚类算法的优点是能够根据需要在不同的尺度上展示对应的聚类结果,缺点同Hierarchical K-means算法一样,一旦两个距离相近的点被划分到不同的簇,之后也不再可能被聚类到同一个簇,即无法撤销先前步骤的工作。
BIRCH算法
CURE算法
Chameleon变色龙算法
这三个放到后面单独出一期讲
拓展