【海量数据挖掘/数据分析】之 贝叶斯信念网络(贝叶斯信念网络、有向无环图、贝叶斯公式、贝叶斯信念网络计算实例)
目录
【海量数据挖掘/数据分析】之 贝叶斯信念网络(贝叶斯信念网络、有向无环图、贝叶斯公式、贝叶斯信念网络计算实例)
一、贝叶斯信念网络
1 . 属性关联 : 贝叶斯信念网络 允许数据集样本属性 之间存在依赖关系 ;
2 . 贝叶斯信念网络 表示方法 :
二、概率图模型 :
马尔科夫假设
三、贝叶斯信念网络 示例 1
四、贝叶斯信念网络 示例 2
1、贝叶斯信念网络 的 有向无环图 表示:
2、贝叶斯信念网络 联合概率分布计算
3、计算 高血压 由 家族史引起的概率
五、贝叶斯信念网络 训练过程
一、贝叶斯信念网络
1 . 属性关联 : 贝叶斯信念网络 允许数据集样本属性 之间存在依赖关系 ;
① 属性概率 : 贝叶斯信念网络中 , 每个节点的概率都可以使用贝叶斯公式计算 ;
贝叶斯公式:P(B|A) = P(AB)/P(A)
② 弧 的 可信度 : 网络中属性之间的 弧 有可信度属性 , 因此将该网络命名为 贝叶斯信念网络 ;
2 . 贝叶斯信念网络 表示方法 :
① 有向无环图 : 使用 有向无环图 表示贝叶斯信念网络 ;
② 随机变量 : 图中的每个节点 , 表示一个随机变量 , 即样本的属性 ;
③ 概率依赖 : 图 ( 有向无环图 ) 中的每条 弧 表示一个概率依赖 , 即样本的一个属性 , 依赖与另外一个属性 ;
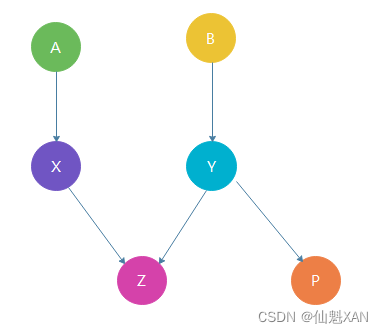
④ 属性概率依赖 : Z 属性依赖与 X 属性 和 Y 属性 , P 属性依赖于 Y 属性 ; 属性 Z 和 属性 P 之间没有依赖关系 ;
特别注意 : 图中一定不能出现环 , 否则就会造成循环依赖 ;
二、概率图模型 :
分为 2 大类 , 一类是有向依赖 , 一类是无向关联 ;
- 贝叶斯信念网络 : 使用 有向无环图 表示 ;
- 马尔科夫网络 : 使用 无向图模型 表示 ;
马尔科夫假设
模型复杂 : 在 贝叶斯信念网络 中 , 如果考虑属性依赖 , 属性 Z 依赖于 属性 X 和 Y 属性 , 属性 X 依赖于 属性 A , 属性 A 依赖于 ⋯ 这样就会导致模型过于复杂 ;
马尔科夫假设 : 为了便于计算 , 每个属性只与其直接依赖的属性有关 , 间接依赖的属性没有直接联系 ;
三、贝叶斯信念网络 示例 1

得肺癌的概率依赖于 是否有家族史 , 是否吸烟 , 两个属性 ;
使用贝叶斯信念网络 的 有向无环图 表示 :

四、贝叶斯信念网络 示例 2
是否有家族病史 属性节点 的 概率表 :

是否有高血脂 属性节点 的 概率表 : 高血脂 属性 依赖于 家族病史属性 :

是否有高血压 属性节点 的 概率表 : 高血压 属性 依赖于 高血脂属性 和 家族病史属性 :
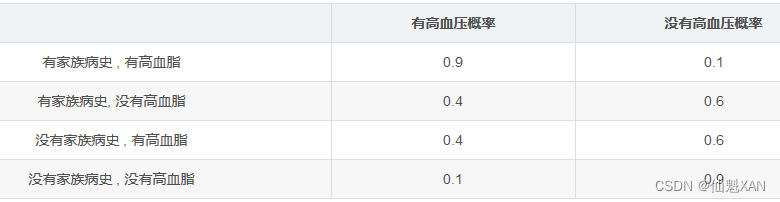
1、贝叶斯信念网络 的 有向无环图 表示:
贝叶斯信念网络中 每个节点都有一个概率表 ;
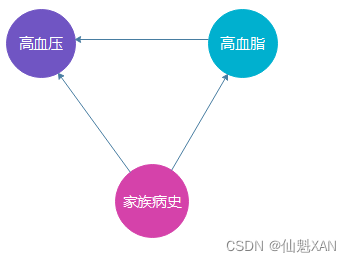
2、贝叶斯信念网络 联合概率分布计算
使用贝叶斯公式计算 ,有 家族病史 , 高血脂 , 高血压 , 三个属性的联合概率分布 ;
P(有家族史,有高血脂,有高血压)
= P(有家族史)×P(有高血脂∣有家族史)×P(有高血压∣有高血脂,有家族史)
= 0.2×0.4×0.9
= 0.072
- P(有家族史) 表示有家族史 的概率 ;
- P ( 有 高 血 脂 ∣ 有 家 族 史 ) P( 有高血脂 | 有家族史 ) P(有高血脂∣有家族史) 表示有家族史 , 并且有高血脂的概率 ;
- P ( 有 高 血 压 ∣ 有 高 血 脂 , 有 家 族 史 ) P ( 有高血压 | 有高血脂 , 有家族史 ) P(有高血压∣有高血脂,有家族史) 表示同时有家族史 和 高血脂 时 , 有高血压的概率 ;
3、计算 高血压 由 家族史引起的概率
① 即计算有家族史时 , 多大概率有高血压 :
P ( 有 高 血 压 ∣ 有 家 族 史 ) = P ( 有 高 血 压 , 有 家 族 史 ) / P ( 有 家 族 史 )
② 概率表中没有 P ( 有 高 血 压 , 有 家 族 史 ) P( 有高血压 , 有家族史 ) P(有高血压,有家族史) 概率 , 需要计算 :
P(有高血压,有家族史)=P(有高血压,有家族史,有高血脂)+P(有高血压,有家族史,无高血脂)
③ 概率表中没有 P ( 有 高 血 压 , 有 家 族 史 , 有 高 血 脂 ) P( 有高血压 , 有家族史 , 有高血脂 ) P(有高血压,有家族史,有高血脂) 概率 , 需要计算
P(有家族史,有高血脂,有高血压)
= P(有家族史)×P(有高血脂|有家族史)×P(有高血压|有高血脂,有家族史)
= 0.2×0.4×0.9
= 0.072
④ 概率表中没有 P ( 有 高 血 压 , 有 家 族 史 , 无 高 血 脂 ) P( 有高血压 , 有家族史 , 无高血脂 ) P(有高血压,有家族史,无高血脂) 概率 , 需要计算 ;
P(有高血压,有家族史,无高血脂)
= P(有家族史)x(无高血脂|有家族史)xP(有高血压|无高血脂,有家族史)
= 0.2×0.6×0.4
= 0.048
⑤ 计算 P ( 有 高 血 压 , 有 家 族 史 ) P( 有高血压 , 有家族史 ) P(有高血压,有家族史) 公式 ② 结果 : 将 ③ 和 ④ 中的计算结果代入到 ② 公式中 :
P(有高血压,有家族史)
= P(有高血压,有家族史,有高血脂)+P(有高血压,有家族史,无高血脂)
= 0.048+0.072
= 0.12
⑥ 计算公式 ① 结果 :
P(有高血压|有家族史)
= P(有高血压,有家族史)/P(有家族史)
= 0.12/0.2
= 0.6
⑦ 结果 : 如果有家族史 , 得高血压的概率是 0.6 ;
五、贝叶斯信念网络 训练过程
1 . 贝叶斯信念网络 模型 使用过程 : 给出训练集 , 通过学习 , 获得 贝叶斯信念网络 , 通过 贝叶斯信念网络 可以推断某个事件发生的概率 ;
2 . 贝叶斯信念网络由 结构 和 参数组成 ;
① 贝叶斯信念网络 结构 : 有向无环图 ;
② 贝叶斯信念网络 参数 : 描述样本间属性依赖关系 , 即每个属性节点对应的条件概率表 ;
3 . 贝叶斯信念网络 机器学习过程 :
① 结构学习 : 确定贝叶斯网络的结构 , 得到有向图 ; 简单的问题可以由人工给出 , 复杂的结构 , 需要计算机给出 ;
② 参数学习 : 最终目的是得到该属性节点的条件概率表 ;
- 贝叶斯网络 B , 结构 G , 参数 Θ , 贝叶斯信念网络可以表示成 B=<G, Θ> ;
- 结构 B 是有向无环图 , 每个节点都代表样本的一个属性 ;
- 如果两个属性由依赖关系 , 使用 有向弧 连接起来 , 箭头由被依赖属性节点 , 指向需要依赖的属性 ;
参考文章
【数据挖掘】贝叶斯信念网络 ( 马尔科夫假设 | 结构 | 有向无环图 | 参数 | 条件概率表 | 案例分析 )_贝叶斯信念网络例题