什么是并查集?
--是一个森林;(由多颗树构成的)
并查集原理
在一些应用问题中,需要
将
n
个不同的元素划分成一些不相交的集合
。
开始时,每个元素自成一个
单元素集合,然后按一定的规律将归于同一组元素的集合合并
。在此过程中
要反复用到查询某一
个元素归属于那个集合的运算
。适合于描述这类问题的抽象数据类型称为
并查集
(union-fifind
set)
。
最开始存-1,表示它们刚开始都是一个集合,十棵树是十个集合

1.像堆类似,用下标表示关系,2。双亲表示法


6,7,8是存它的父亲,假设0是6的父亲,把6的-1加到0那里,之后存父亲的下标,0下面变成-2,6变成0;
特点:1.如果一个位置的值是负数,那它就是这个树的根,这个复数的绝对值就是这棵树数据的个数;2.一个位置值是正数,那它就是双亲的下标;

如果想合并两个树形成一个新树该怎么办?
(1合并到0也可以,0合并到1也可以,并查集这里没有严格规定)

class UnionFindSet
{
public:
UnionFindSet(size_t n)
:_ufs(n, -1)
{}
void Union(int x1, int x2)
{
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2)//如果本身在一个集合,就没必要合并
{
return;
}
if (root1 > root2)//如果想用小的去合并大的;
swap(root1, root2);
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
int FindRoot(int x)
{
int parent = x;
while (_ufs[parent] >= 0)
{
parent = _ufs[parent];
}
return parent;
}
bool InSet(int x1,int x2)//是不是在同一个集合
{
return FindRoot(x1) == FindRoot(x2);
}
size_t SetSize()
{
//有几个值是复数就有几个根节点
size_t size = 0;
for (size_t i = 0; i < _ufs.size(); ++i)
{
if (_ufs[i] < 0)
{
++size;
}
}
return size;
}
private:
vector<int> _ufs;
};
/*class UnionFindSet
{
public:
UnionFindSet(size_t n)
:_ufs(n, -1)
{}
void Union(int x1, int x2)
{
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2)//如果本身在一个集合,就没必要合并
{
return;
}
if (root1 > root2)//如果想用小的去合并大的;
swap(root1, root2);
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
int FindRoot(int x)
{
int parent = x;
while (_ufs[parent] >= 0)
{
parent = _ufs[parent];
}
return parent;
}
bool InSet(int x1,int x2)//是不是在同一个集合
{
return FindRoot(x1) == FindRoot(x2);
}
size_t SetSize()
{
//有几个值是复数就有几个根节点
size_t size = 0;
for (size_t i = 0; i < _ufs.size(); ++i)
{
if (_ufs[i] < 0)
{
++size;
}
}
return size;
}
private:
vector<int> _ufs;
};
class Solution {
public:
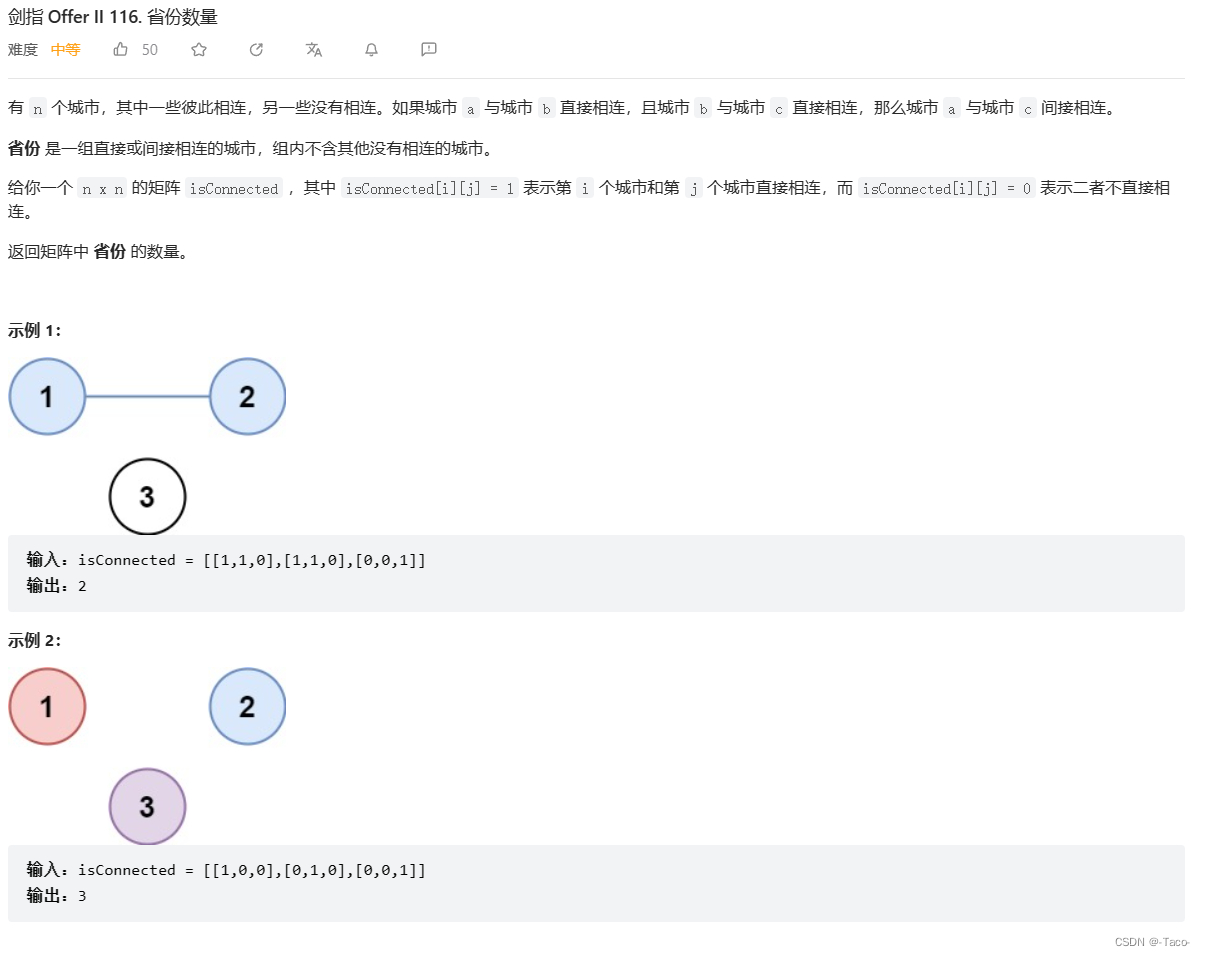
int findCircleNum(vector<vector<int>>& isConnected) {
UnionFindSet ufs(isConnected.size());
for(int i=0;i<isConnected.size();i++)
{
for(int j=0;j<isConnected[i].size();++j)
{
if(isConnected[i][j]==1)
{
ufs.Union(i,j);
}
}
}
return ufs.SetSize();
}
};
*/
//手动写一个并查集还是比较麻烦的,这里借助并查集的思想现场写一个合并
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
vector<int> ufs(isConnected.size(),-1);
auto findroot=[&ufs](int x)
{
while(ufs[x]>=0)
x=ufs[x];
return x;
};
for(int i=0;i<isConnected.size();i++)
{
for(int j=0;j<isConnected[i].size();++j)
{
if(isConnected[i][j]==1)
{
int root1=findroot(i);
int root2=findroot(j);
if(root1!=root2)
{
ufs[root1]+=ufs[root2];
ufs[root2]=root1;
}
}
}
}
int n=0;
for(auto e:ufs)
{
if(e<0)
++n;
}
return n;
}
};再浅谈一下压缩路径的问题,如果一直合并,合并的层数很多的情况下,这样就需要重新梳理它的逻辑,就把它层数由原来的很多层,可以直接变成一层,这就是压缩路径,一般数据量不是很大的情况下,就不需要这样压缩;