对弈人工智能！myCobot 280开源六轴机械臂Connect 4 四子棋对弈

Connect 4 myCobot280

Introduction

Hi,guys.今天我们来介绍一下人工智能下棋，我们将用机械臂来作为对手跟你进行下棋。

人工智能下棋的研究可以追溯到20世纪50年代。当时，计算机科学家开始探索如何编写程序，使计算机能够下象棋。其中最著名的例子是由IBM研发的Deep Blue，它在1997年以3.5-2.5的成绩击败了当时的世界象棋冠军加里·卡斯帕罗夫。

人工智能下棋，就好像给电脑一个思考的方式让它在比赛中取得胜利。这个思考的方式有很多种，大多数都源于优秀的算法。Deep Blue的核心算法是基于暴力穷举：生成所有可能的走法，然后执行尽可能深的搜索，并不断对局面进行评估，尝试找出最佳走法。

今天我将要介绍一款AI机械臂下棋是如何来实现的。

Connect 4

Connect4是今天要介绍的一种策略棋类游戏，也被称为是四子棋。Connect4的游戏目标是在一个垂直放置的6行7列网格中先达成连续四个棋子的横向、纵向或斜向排列。两名玩家轮流在网格的顶部插入自己的棋子，棋子会落到当前列的最底部可用的位置。玩家可以选择将自己的棋子放置在任意一列，但棋子只能被放置在已有棋子下方的位置。

就如动图中所示，这就是connect4。

myCobot 280

机械臂这边选择的是myCobot 280 M5Stack，它是一款功能强大的桌面型六轴机械臂，它采用M5Stack-Basic作为控制核心，支持多种编程语言开发。Mycobot280的六轴结构使其具有高度的灵活性和精度，能够进行各种复杂的操作和运动。它支持多种编程语言，包括Python、C++、Java等，使开发者能够根据自己的需求对机械臂进行编程和控制。它的简单操作界面和详细的用户手册使得用户能够快速上手，而且其嵌入式设计使得机械臂的体积小巧，易于携带和存储。

下面是我们搭建的场景。

用myCobot来作为人工智能来跟我们进行下棋。

对弈算法

首先，我们得解决一个最关键的问题，就是应该用什么算法来进行对弈。换句话说就是给机械臂提供一个能够进行思考的大脑。我们将为你简单介绍几种常见的对弈算法：

极小化极大算法：

这是一种经典的博弈算法，适用于两人对弈的游戏。它通过递归地模拟对手和自己的行动，评估每个可能的走法的得分，并选择具有最优得分的行动。极小化极大算法可以通过搜索棋局的树状结构来找到最佳的下棋策略。该算法是一个零总和算法，即一方要在可选的选项中选择将其优势最大化的选择，另一方则选择令对手优势最小化的方法。而开始的时候总和为0。简单举例井字棋说明一下。

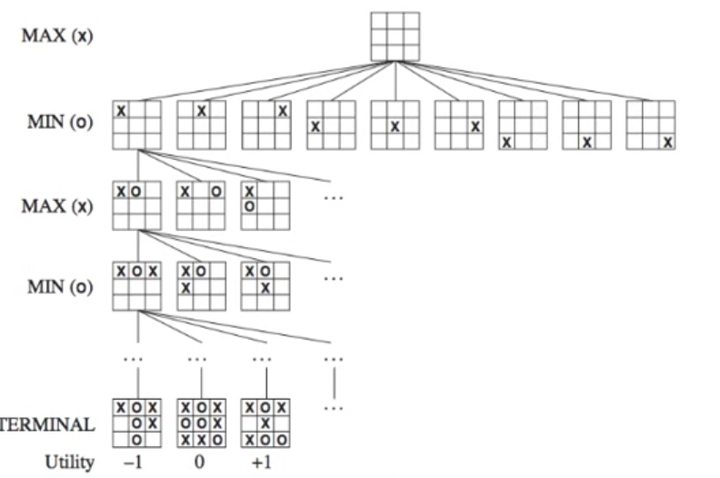
Max代表我们，Min代表对手。这个时候我们需要给每一种结果一个分数，就是这里的Utility。这个分数是站在我们（也就是Max）的角度评估的，比如上图中我赢了就是＋1，输了是－1，平局时0。所以，我们希望最大化这个分数，而对手希望最小化这个分数。（在游戏中，这个分数被称为static value。）这里要说一下，井字棋是个比较简单的游戏，所以可以列出所有可能的结果。但是，大部分游戏是不太可能把所有结果都列出来的。根据计算机运算量，我们可能只能往前推7，8步，所以这个时候分数就不只－1，1，0这么简单了，会有专门的算法来根据当前结果给不同的分数。

Alpha-Beta剪枝算法：

这是对极小化极大算法的优化。它通过剪枝来减少搜索的分支数，从而加快搜索速度。Alpha-Beta剪枝算法利用上下界（Alpha和Beta值）来判断哪些分支可以被丢弃，从而减少搜索的深度。

神经网络+深度学习：

我们设计的对弈算法connect4中用到的也是神经网络+深度学习来解决对弈的算法。

神经网络：

科学家一直希望模拟人的大脑，造出可以思考的机器。人为什么能够思考？科学家发现，原因在于人体的神经网络。神经网络是一种模拟人脑神经系统结构和功能的数学模型，通过模拟神经元之间的连接和信号传递来进行信息处理和学习。神经网络是一切人工智能的开始。

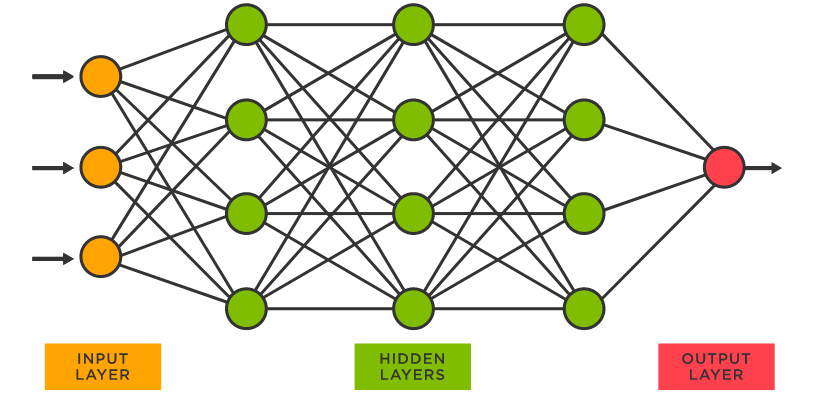
神经网络算法的基本思想是将输入数据传递给网络的输入层，然后通过一系列中间层（隐藏层）的计算和传递，最终得到输出层的结果。训练过程通过调整连接权重来最小化实际输出与期望输出之间的差异，以优化网络的性能。

深度学习：

深度学习是一种机器学习的分支，专注于利用深度神经网络进行学习和推理。深度学习通过构建深层次的神经网络，也就是有多个中间层（隐藏层）的神经网络，来解决复杂的学习和决策问题。可以说深度学习是利用神经网络作为核心工具的一种学习方法。深度学习不仅包括了神经网络的结构和算法，还包括了训练方法、优化算法和大规模数据处理等方面的内容。

项目的构建

项目主要分为，硬件和软件两个部分：

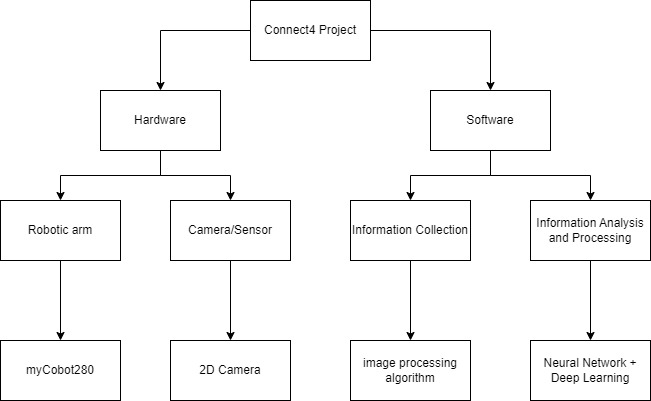
该项目中最为重要的就是信息收集和信息分析和处理这一部分内容。

前面也提到了神经算法和深度学习的相关知识，我们使用到的是DQN神经网络。

DQN神经网络

DQN神经网络是由DeepMind公司提出的，它结合了深度学习和强化学习的思想。DQN通过使用深度神经网络来估计状态-动作值函数（Q函数），从而实现对复杂环境中的最优决策DQN的核心思想是使用深度神经网络作为函数逼近器来近似状态-动作值函数。通过将当前状态作为输入，神经网络输出每个动作的对应Q值，即预测该动作在当前状态下的长期回报。然后，根据Q值选择最优的动作进行执行。

环境搭建

首先我们要定义Connect4这个游戏，用一个二维数组表示游戏棋盘，两种颜色的棋子，红色R，黄色Y。再定义游戏结束的条件，当有四个统一颜色的棋子连成一线就退出游戏。

#Define a 6*7 chessboard
self.bgr_data_grid = [[None for j in range(6)] for i in range(7)]

#Used to display the state of the board
def debug_display_chess_console(self):
    for y in range(6):
        for x in range(7):
            cell = self.stable_grid[x][y]
            if cell == Board.P_RED:
                print(Board.DISPLAY_R, end="")
            elif cell == Board.P_YELLOW:
                print(Board.DISPLAY_Y, end="")
            else:
                print(Board.DISPLAY_EMPTY, end="")
        print()
    print()

复制

下面是定义游戏是否结束的code：

def is_game_over(board):
    # Check if there are four consecutive identical pieces in a row.
    for row in board:
        for col in range(len(row) - 3):
            if row[col] != 0 and row[col] == row[col+1] == row[col+2] == row[col+3]:
                return True

    # Check if there are four consecutive identical pieces in a column.
    for col in range(len(board[0])):
        for row in range(len(board) - 3):
            if board[row][col] != 0 and board[row][col] == board[row+1][col] == board[row+2][col] == board[row+3][col]:
                return True

    # Examine if there are four consecutive identical pieces in a diagonal line.
    for row in range(len(board) - 3):
        for col in range(len(board[0]) - 3):
            if board[row][col] != 0 and board[row][col] == board[row+1][col+1] == board[row+2][col+2] == board[row+3][col+3]:
                return True

    for row in range(len(board) - 3):
        for col in range(3, len(board[0])):
            if board[row][col] != 0 and board[row][col] == board[row+1][col-1] == board[row+2][col-2] == board[row+3][col-3]:
                return True

    # Verify if the game board is filled completely.
    for row in board:
        if 0 in row:
            return False

    return True

复制

构建DQN神经网络

定义神经网络的输入层和输出层，其中输入层的维度应与游戏板的状态表示方式相匹配，输出层的维度应与合法动作的数量相匹配。简而言之，输入层接受游戏棋盘的状态信息，输出层产生对应的动作选择。

经验缓存区

机器是需要学习，我们要构建一个经验缓存区，来存储智能体的经验。这可以是一个列表或队列，用于存储游戏过程中的状态、动作、奖励和下一个状态等信息。

下面是构建经验缓存区的伪代码：

class ReplayBuffer:
    def __init__(self, capacity):
        self.capacity = capacity
        self.buffer = []

    def add_experience(self, experience):
        if len(self.buffer) >= self.capacity:
            self.buffer.pop(0)
        self.buffer.append(experience)

    def sample_batch(self, batch_size):
        batch = random.sample(self.buffer, batch_size)
        states, actions, rewards, next_states, dones = zip(*batch)
        return states, actions, rewards, next_states, dones

复制

决策

我们定义了一个名为EpsilonGreedyStrategy的策略类，使用ε-greedy策略进行动作选择和探索。在初始化函数__init__()中，我们指定了探索率ε。select_action()方法根据Q值选择动作，根据探索率的概率随机选择动作或选择具有最高Q值的动作。

class EpsilonGreedyStrategy:
    def __init__(self, epsilon):
        self.epsilon = epsilon

    def select_action(self, q_values):
        if random.random() < self.epsilon:
            action = random.randint(0, len(q_values) - 1)
        else:
            action = max(enumerate(q_values), key=lambda x: x[1])[0]
        return action

复制