从零开始系列之PID控制,宗旨就是以说人话的方式讲述它,真正的做到从零开始,小白一看就会,一学就废。
一、什么是PID控制?
PID控制(比例-积分-微分控制)由比例单元(Proportional)、积分单元(Integral)和微分单元(Derivative)组成。可以通过调整这三个单元的增益系数 Kp、Ki和Kd来调定其特性。
PID控制是一个在工业控制应用中常见的反馈控制。通过把实际采集到的数据和一个设定的目标值进行比较,得到误差值,然后把误差值用于计算出新的输入值,这个新的输入值的目的是可以让系统输出的实际数据达到或者保持在设定的目标值。PID控制器可以根据历史数据和差别的出现率来调整输入值,使系统更加准确而稳定。主要适用于基本上线性,且动态特性不随时间变化的系统。
控制的逻辑图如下:
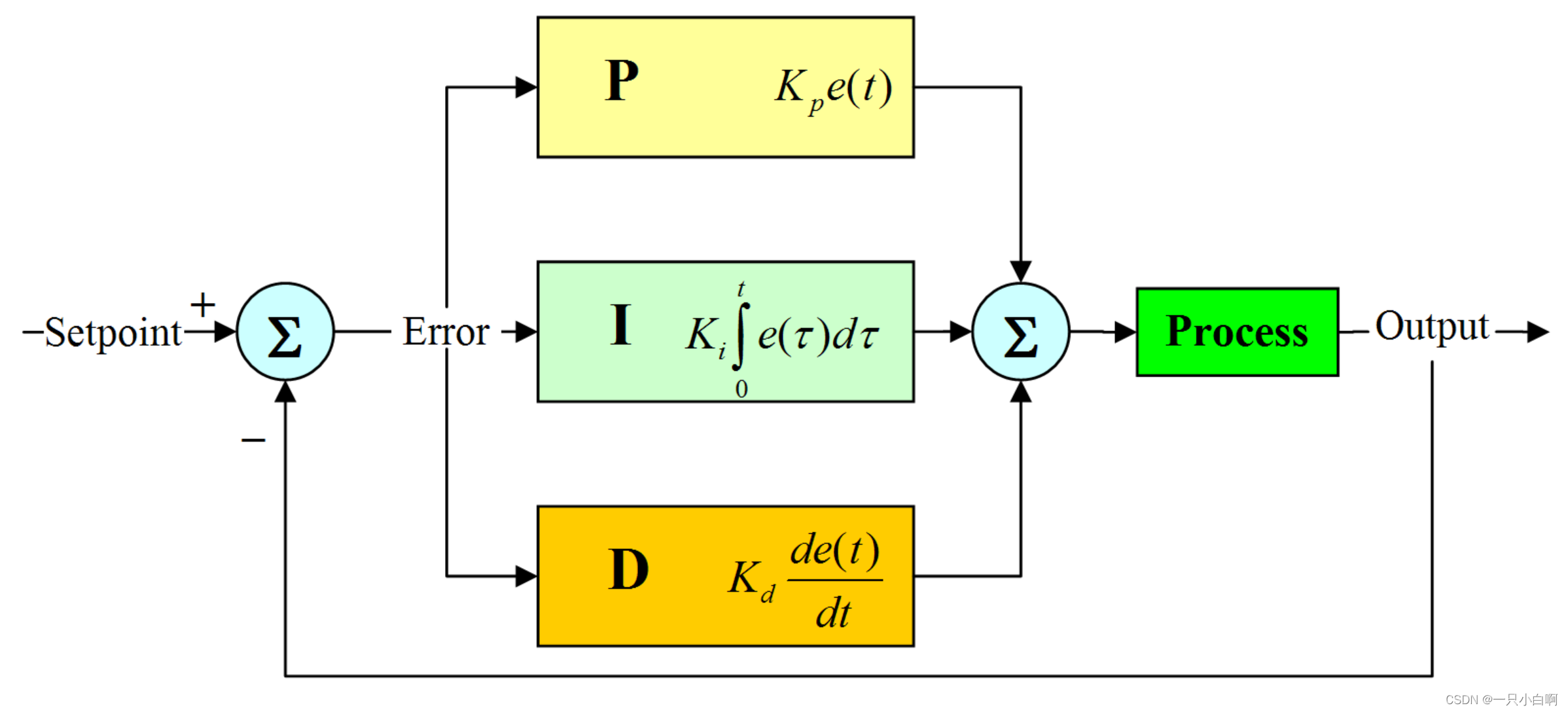
举个例子,在一个电压源的系统中,我需要一个5V的输出电压,此时设定输入r(t) = 5,假如此时输出为0V,那么此时的误差e(t)= -5,然后通过下面公式计算出u(t),给到输出,然后重复之前的步骤直到误差e(t) = 0,就达到了最终的控制目的。
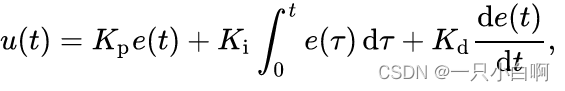
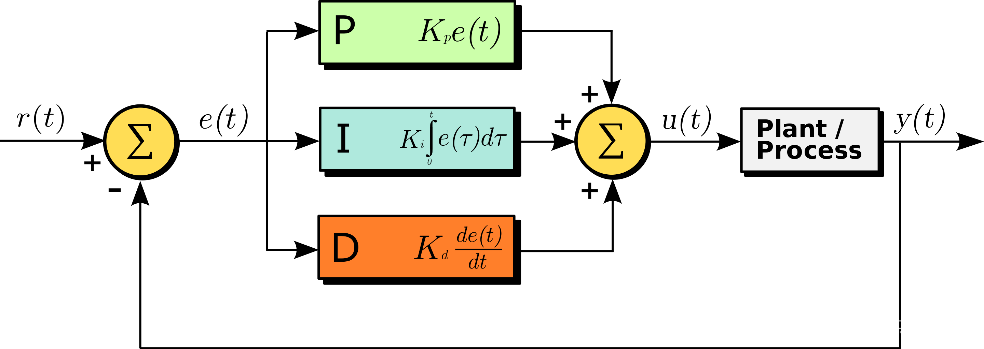
二、PID参数
1.参数含义:
P:比例项,误差值和一个正值的常数Kp(表示比例)相乘。
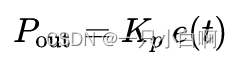
Kp只是在控制器的输出和系统的误差成比例的时候成立。比如,一个电热器控制器是在目标温度和实际温度差10°C时有100%的输出,而其目标值是25°C。那么它在15°C的时候会输出100%,在20°C的时候会输出50%,在24°C的时候输出10%,注意在误差是0的时候,控制器的输出也是0,若要让受控输出为非零的数值,就需要产生一个稳态误差或偏移量。
若比例增益大,在相同误差量下,会有较大的输出,但若比例增益太大,会使系统不稳定。相反的,若比例增益小,若在相同误差量下,其输出较小,因此控制器会较不敏感的。若比例增益太小,当有干扰出现时,其控制信号可能不够大,无法修正干扰的影响。
当比例系数Kp=1时,y=x(这里x = e(t),y = Pout),Kp越大,斜率越大。输出与误差信号成正比,换句话说,比例控制器的输出是误差信号和比例增益的乘积。
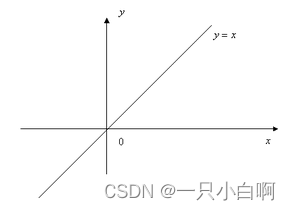
比例项的作用是调节系统的响应速度,增大比例增益可以提高系统的响应速度,但可能导致不稳定性;减小比例增益可以增加系统的稳定性,但可能导致响应速度过慢。
本身无法完全消除稳态误差,因为比例控制是一种线性反馈控制,其输出与误差成正比,只根据当前的误差大小产生控制输出,而无法纠正已经累积的误差。
I:积分项,积分控制考虑过去误差,将过去一段时间的误差值总和乘以一个正值的常数Ki。
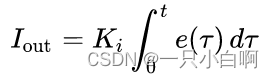
这里的积分被称为定积分,它可以被解释为平面上区域的带符号的面积,该区域由给定函数在实直线上两点之间的图形所包围。通常,平面横轴以上的面积为正,而平面横轴以下的面积为负。

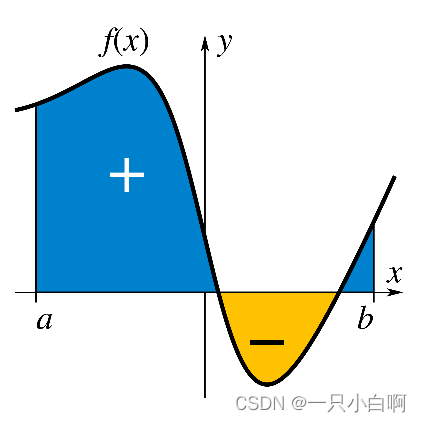
积分是对误差随时间的累积,如果应用比例控制后存在残余误差,则积分项试图通过添加由于误差的历史累积值而产生的控制效应来消除残余误差。当误差消除后,积分项将停止增长。
D:微分项,考虑将来误差,计算误差的一阶导,乘以一个正值的常数Kd。
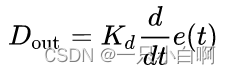
这个导数的控制会对系统的改变作出反应。导数的结果越大,那么控制系统就对输出结果作出更快速的反应。这个Kd参数也是PID被称为可预测的控制器的原因。Kd参数对减少控制器短期的改变很有帮助。一些实际中的速度缓慢的系统可以不需要Kd参数。
求导的过程称为微分,在数学中,导数表示函数的输出相对于输入变化的敏感性。导数是微积分的基本工具。例如,运动物体的位置相对于时间的导数是物体的速度:它测量的是随着时间的推移物体的位置变化有多快。
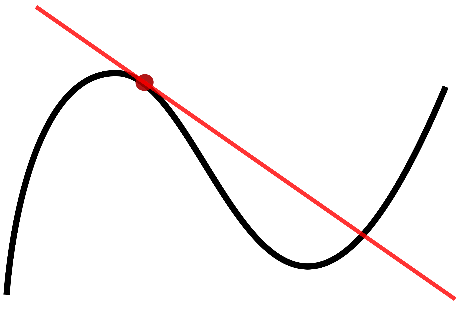
微分项根据误差的变化率来调整控制输出,帮助预测系统输出的趋势,并对输出的变化率进行调整。
2.参数概述
PID控制器的比例单元(P)、积分单元(I)和微分单元(D)分别对应目前误差、过去累计误差及未来误差。若是不知道受控系统的特性,一般认为PID控制器是最适用的控制器。
控制器的响应可以用控制器对误差的反应快慢、控制器过冲的程度及系统震荡的程度来表示。
不过使用PID控制器不一定保证可达到系统的最佳控制,也不能保证系统稳定性。有些应用只需要PID控制器的部分单元,可以将不需要单元的参数设为零即可。
因此PID控制器可以变成PI控制器、PD控制器、P控制器或I控制器。其中又以PI控制器比较常用,因为D控制器对回授噪声十分敏感,而若没有I控制器的话,系统不会回到参考值,会存在一个误差量。
总而言之,比例项提供快速的响应,积分项消除稳态误差,微分项改善系统的动态响应,综合使用比例、积分和微分三个控制项从而实现高效、稳定的控制性能。但在实际应用中,需要根据具体系统的特性和需求,合理选择和调节PID控制器的增益参数,以达到最优的控制效果。
三、实现一个简单的PID控制算法
1、实现步骤如下
- 计算误差,error=设定值-实际值。
- 计算比例值,P= Kp * error
- 计算积分值,I= Ipre + Ki * Ts * error
- 计算微分值,D= Kd * (error – error_pre)/ Ts
- 计算PID值,PID = P + I + D
- 将PID值输出到控制器。
- 重复上面的步骤。
2、实际使用注意
实际在实现上述步骤的时候,还会有一些问题,毕竟不能以理想情况考虑,比如,
1、积分饱和
若设定值有大的变动,其积分量会有大幅的变化,大到输出值被上下限限制而饱和,因此系统会有过冲,而且即使误差量符号改变,积分量变小,但输出值仍被上下限限制,维持在上限(或下限),因此输出看似没有变化,系统仍会持续的过冲,一直要到输出值落在上下限的范围内,系统的回授量才会开始下降。此问题可以用以下方式处理:
- 在程序变数离开可控制范围时,暂停积分
- 让积分值限制在一个较小的上下范围内
- 重新计算积分项,使控制器输出维持上下限之间的范围内
积分饱和讲人话方式:还是上面那个电压源,当设定值突然很大(10000V),这时积分项会超出输出值很多(10000V以上),在后面的调节中,比如设定输出电压为3V时,首先要将积分值(10000V以上)调到输出值范围(0-5V)后,才能对实际的控制进行调节,最后达到3V。
2、输出饱和
PID输出值太大/小,超过实际控制值的范围,有些执行器可能无法识别这个控制值,会产生两种状态:控制无效,保持当前值不变、输出一个最大/最小控制状态。
3、输出变化太快。
设定一个目标值后,PID输出值变化率很大,在一些反应比较慢的滞后系统或者状态改变不能突变的系统中,需要对这个变化率做限制,以免变化太快导致机器损坏或者造成其他危险。
4、等等。
3、c语言例程
计算部分如下:
// 1、计算误差
float error = pid_handle->set_value - _sample_value;
// 2、计算比例系数
float proportional = pid_handle->P * error;
// 3、计算积分系数
// time_interval * 0.5f 是为了在离散时间积分中使用梯形规则(Trapezoidal Rule)进行数值积分。该方法使用当前时间间隔的一半来估计误差的变化率,并将其与之前的误差相加
float integral = pid_handle->integral_prev + pid_handle->I * time_interval * 0.5f * (error + pid_handle->error_prev);
// 4、限值积分项的取值范围,避免积分项过大或过小导致系统不稳定或响应不正确的问题
integral = pid_data_constrain(integral, -pid_handle->output_max, pid_handle->output_max);
// 5、计算微分项
float derivative = pid_handle->D * (error - pid_handle->error_prev) / time_interval;
// 6、计算输出值
float output = proportional + integral + derivative;
// 7、限值输出值
output = pid_data_constrain(output, -pid_handle->output_max, pid_handle->output_max);
// 8、输出变化率限制
if (pid_handle->output_ramp > 0)
{
float output_rate = (output - pid_handle->output_prev) / time_interval;
if (output_rate > pid_handle->output_ramp)
output = pid_handle->output_prev + pid_handle->output_ramp * time_interval;
else if (output_rate < -pid_handle->output_ramp)
output = pid_handle->output_prev - pid_handle->output_ramp * time_interval;
}
// 9、存储当前值
pid_handle->integral_prev = integral;
pid_handle->output_prev = output;
pid_handle->error_prev = error;
pid_handle->times_prev = times_now;
// 10、更新输出值
pid_handle->output_value = output;四、调参方法
1、人工调参
这个就不用多说了,需要对PID的参数有一定的理解。
有一种通用的方法如下:先将Ki及Kd设为零,增加Kp一直到回路输出震荡为止,之后再将Kp设定为“1/4振幅衰减”(使系统第二次过冲量是第一次的1/4)增益的一半,然后增加Ki直到一定时间后的稳态误差可被修正为止。不过若Ki可能会造成不稳定,最后若有需要,可以增加Kd,并确认在负载变动后回路可以够快的回到其设定值,不过若Kd太大会造成响应太快及过冲。一般而言快速反应的PID应该会有轻微的过冲,只是有些系统不允许过冲。因此需要将控制系统调整为过阻尼系统。

2、齐格勒-尼科尔斯方法
一种启发式的调试方式,由John G. Ziegler和Nathaniel B. Nichols在1940年代导入,一开始也是将Ki及Kd设定为零,增加Kp比例增益直到系统开始等振幅振荡为止,当时的增益称为Ku,而振荡周期为Pu,即可用以下的方式计算增益:
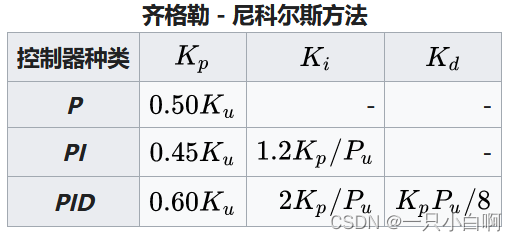
五、PID控制举例
用excle设计了一个PID控制系统,PID输出直接作用于执行器,执行器1:1输出。可自行下载文件体验调参,文件链接:PID控制数据例程.xlsx - 蓝奏云
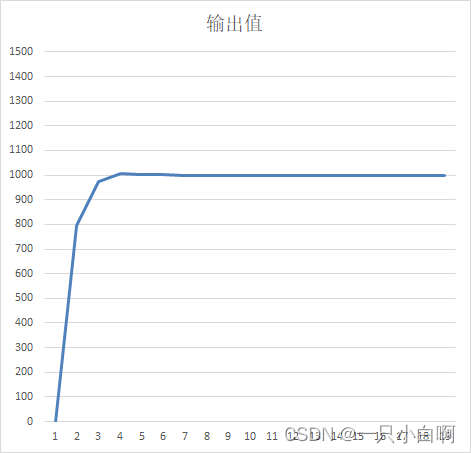
设定一个输入值后,通过调节PID系数,观察输出值的图表,文件内容:
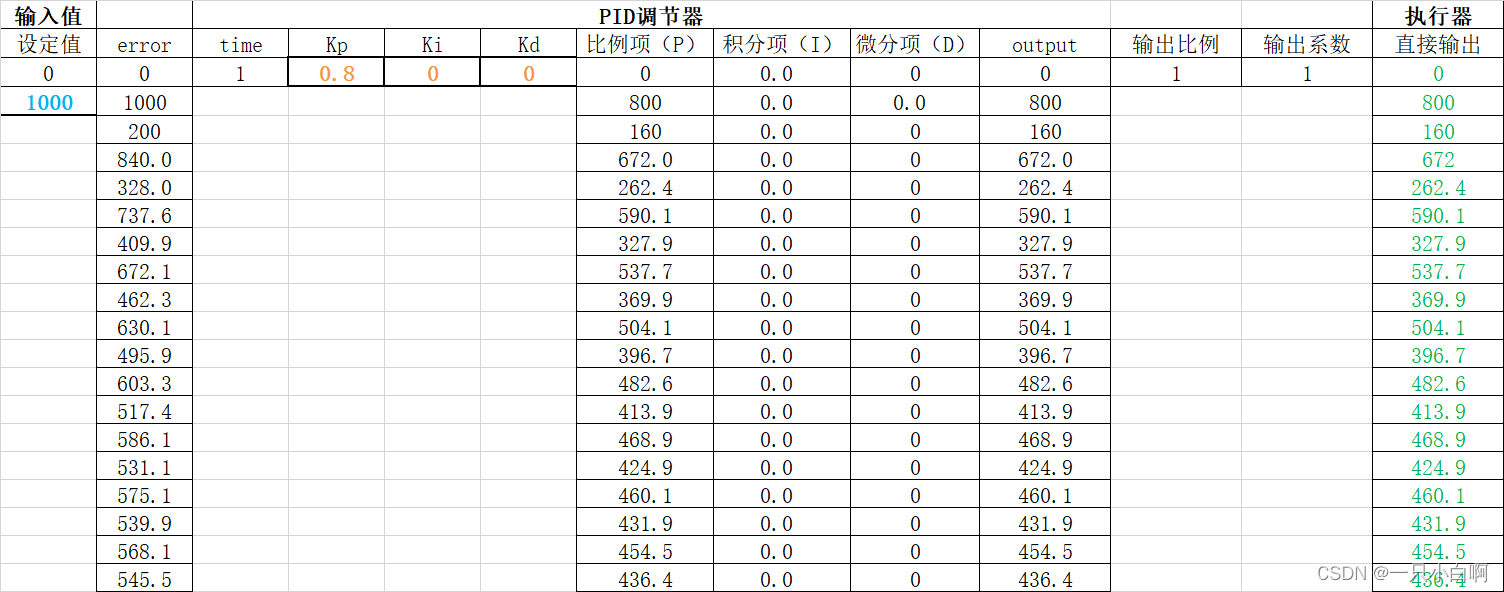
参数为Kp = 0.8、Ki = 0、Kd = 0时,输出如下图:
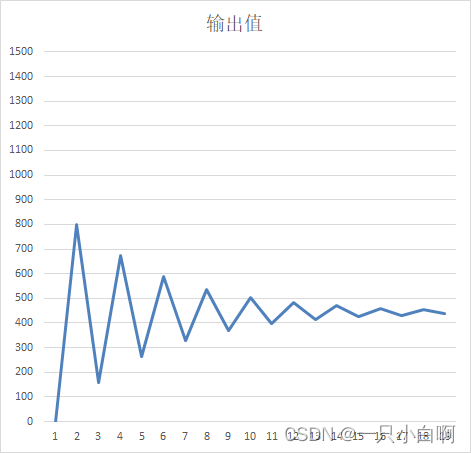
参数为Kp = 0.8、Ki = 0.5、Kd = 0时,输出如下图:
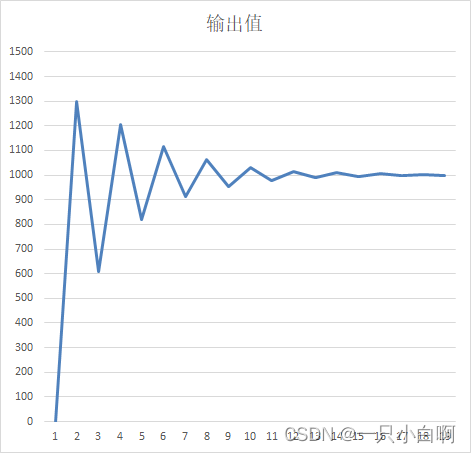
参数为Kp = 0.38、Ki = 0.41、Kd = 0.007时,输出如下图: