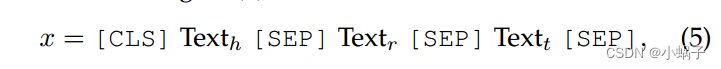从零开始备战数学建模国赛之线性规划1.1
现在距离2023年的数学建模国赛还有不足三个月的时间,想与大家共同备战国赛。
这是我自己总结的一些代码和资料(本文中的代码以及参考书籍等),放在github上供大家参考:https://github.com/HuaandQi/Mathematical-modeling.git
1.什么是线性规划?
线性规划(Linear Programming,LP)是数学建模中常见的优化问题之一。它的目标是在给定的线性约束条件下,寻找一组变量的取值,使得线性目标函数达到最大或最小值。
线性规划问题可以用以下标准形式表示:
最小化:C^T * X
约束条件:A * X <= B
X >= 0
其中,C是目标函数的系数向量,X是待求解的变量向量,A是约束条件的系数矩阵,B是约束条件的右侧向量。
2.实战
关于概念,这里不做过多的赘述,我们直接从题目实战提升结题能力。
2.1 题目1
(1)问题:

(2)解题思路:
先对方程式进行化简成以下形式:
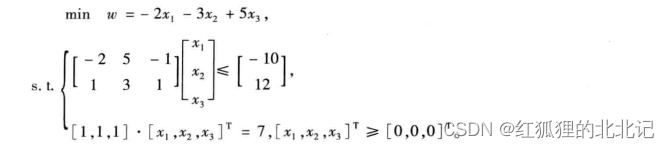
(3)求解的python程序如下:
from scipy.optimize import linprog
# 定义目标函数的系数向量
c = [-2, -3, 5]
# 定义约束条件的系数矩阵
A = [[1, 1, 1],
[-2, 5, -1],
[-1, -3, -1]]
# 定义约束条件的右侧向量
b = [7, -10, -12]
# 定义变量的取值范围
x_bounds = [(0, None), (0, None), (0, None)]
# 求解线性规划问题
res = linprog(c, A_ub=A, b_ub=b, bounds=x_bounds, method='simplex')
# 提取最优解和最大值
z_max = res.fun
x_opt = res.x
# 输出结果
print("最大值 z = {:.4f}".format(z_max))
print("最优解 x1 = {:.4f}".format(x_opt[0]))
print("最优解 x2 = {:.4f}".format(x_opt[1]))
print("最优解 x3 = {:.4f}".format(x_opt[2]))
(4)运行结果:
最大值 z = -14.5714
最优解 x1 = 6.4286
最优解 x2 = 0.5714
最优解 x3 = 0.0000
2.2 题目2
(1)问题:
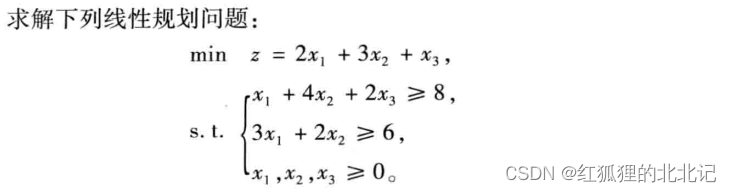
(2)程序:
from scipy.optimize import linprog
# 定义目标函数的系数向量
c = [2, 3, 1]
# 定义约束条件的系数矩阵
A = [[-1, -4, -2],
[-3, -2, 0]]
# 定义约束条件的右侧向量
b = [-8, -6]
# 定义变量的取值范围
x_bounds = [(0, None), (0, None), (0, None)]
# 求解线性规划问题
res = linprog(c, A_ub=A, b_ub=b, bounds=x_bounds, method='simplex')
# 提取最优解和最优值
z_min = res.fun
x_opt = res.x
# 输出结果
print("最小值 z = {:.4f}".format(z_min))
print("最优解 x1 = {:.4f}".format(x_opt[0]))
print("最优解 x2 = {:.4f}".format(x_opt[1]))
print("最优解 x3 = {:.4f}".format(x_opt[2]))
(3)运行结果
最小值 z = 7.0000
最优解 x1 = 0.8000
最优解 x2 = 1.8000
最优解 x3 = 0.0000
3.结语
后续持续更新…
更多代码和资料在github上:https://github.com/HuaandQi/Mathematical-modeling