原创 | 文 BFT机器人

01
背景
在非刚性点云匹配领域,将两个或多个形状的点云对应起来是一个具有挑战性的任务。在这个问题中,形状的变形可能会导致点云之间的几何形状和拓扑结构的差异。因此,点云匹配方法需要能够识别和建立这些非刚性变形下的对应关系。
以往的点云匹配方法通常依赖于手工设计的特征描述符或采用迭代优化的方法。然而,这些方法往往对数据的特征表示和模型的选择非常敏感,并且需要大量的标记数据或结构几何信息来进行监督。此外,许多方法还依赖于离线基础构建的步骤,这增加了算法的复杂性和计算成本。
为了解决这些问题,论文提出了一种名为神经内在嵌入(Neural Intrinsic Embedding,简称NIE)的方法来进行非刚性点云匹配。NIE的目标是通过学习将点云的顶点嵌入到高维空间中,同时保留形状的内在结构。为了实现这一目标,NIE通过训练来逼近点云表面上对应点之间的测地距离。通过这种方式,NIE能够学习到点云之间的非刚性变形,并将其编码为高维嵌入空间中的向量表示。。
通过在实验中与现有的点云匹配方法进行比较,论文展示了NIE的有效性。实验结果表明,NIE在不同数据集和场景下都能取得与或优于现有方法的性能,同时不需要更多的监督信息或结构几何输入。这证明了NIE在非刚性点云匹配中的潜力和优越性。
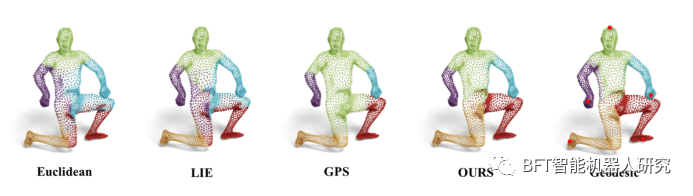
图1 点云分割成具有内在几何感知的聚类
02
算法介绍
这篇论文的研究背景主要涉及到功能映射(functional maps)和线性不变嵌入(linear invariant embedding)等相关概念。功能映射是一种点对点映射的替代表示方法,它主要基于拉普拉斯-贝尔特拉米算子的特征基。给定一对形状S1和S2,首先计算它们的前k个特征函数,并将它们存储为矩阵Φi ∈ Rni×k,其中i = 1, 2 。线性不变嵌入(LIE)是另一种与我们的框架密切相关的方法。
本论文提出的方法与LIE不同之处在于:
(1)对形状之间的对应关系没有监督;
(2)在几何上提供了更多的信息;
(3)与LIE不同,即使在小规模数据集上训练也能很好地推广。
论文中提出的算法称为神经内在嵌入(Neural Intrinsic Embedding,简称NIE)。它旨在解决在可变形形状的点云之间建立对应关系的挑战。NIE旨在将点云的每个顶点嵌入到高维空间中,同时保持底层对象的内在结构。通过训练NIE来逼近表面上对应点之间的测地距离,实现了这种嵌入。
基于NIE,该论文进一步提出了一种非刚性点云配准的弱监督学习框架。与以前需要大量和敏感的离线基础构建的方法不同,NIE不依赖这种过程。所提出的框架不需要基于地面真实对应标签进行监督。通过实验证明了该框架的有效性,结果显示与需要更多监督和/或结构几何输入的最先进基线方法相比,性能相当或更好。
03
论文的创新点
1. 提出了一种新的非刚性点云匹配方法,称为神经内在嵌入(Neural Intrinsic Embedding,NIE)。与现有的方法相比,NIE能够更好地保留点云的内在结构,从而实现更准确的匹配。
2. 提出了一种新的点云嵌入方法,称为点云自适应嵌入(Point Cloud Adaptive Embedding,PCAE)。PCAE能够自适应地学习点云的嵌入表示,从而更好地捕捉点云的几何特征。
3. 提出了一种新的点云对齐方法,称为点云对齐网络(Point Cloud Alignment Network,PCAN)。PCAN能够将两个点云嵌入到同一空间中,并通过最小化它们之间的距离来实现点云对齐。
04
实验
1.评估了学习到的嵌入表示,并提供了消融研究来验证他们提出的设计。他们通过比较不同的实验设置和参数选择来分析嵌入表示的性能。
2.展示了他们提出的NIM网络的匹配结果,并将其与几种竞争性的基线方法进行了比较。他们使用平均测地误差来评估匹配结果,这些结果是在形状归一化到单位面积的情况下仅使用点云进行推断时得出的。
3.展示了他们的NIE和NIM网络对于噪声和各种局部性等伪影的鲁棒性。他们通过引入不同类型的伪影来评估网络的鲁棒性,并分析其对匹配结果的影响。
在实验部分,作者提供了使用的数据集的详细信息,包括FAUST数据集的重新网格化版本和包含100个人体形状的训练和测试集的划分。
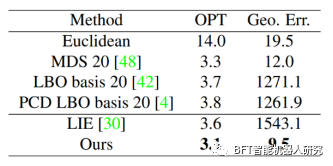
表1 不同方法在基础数据集上的比较结果
表1提供了不同方法在基础数据集上的比较结果,包括OPT(×100)和相对测地误差(x100)。该表格显示了不同方法在这两个指标上的性能。其中,"Ours"指的是该论文提出的方法,"MDS"是多维缩放方法,"LBO basis"和"PCD LBO basis"是基于LBO的方法,"LIE"是基于正交约束的方法。从表格中可以看出,该论文提出的方法在OPT和相对测地误差方面都表现最佳。
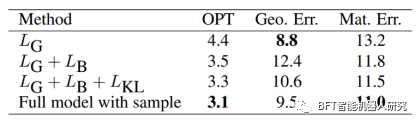
表2 关于训练损失的消融研究结果
表2提供了关于训练损失的消融研究结果,包括OPT(×100)、相对测地误差(x100)和最终匹配误差(x100)。该表格显示了在不同训练损失项和修改后的DGCNN上进行的实验的结果。以下是表格中的结果:
- 使用仅相对测地损失时,虽然可以获得最低的误差,但NIE存在秩缺失问题,导致最差的OPT得分。
- 使用相对测地损失和时,可以获得更好的OPT和相对测地误差。
- 使用相对测地损失、和时,可以进一步改善OPT和相对测地误差。
- 使用包含样本的完整模型时,可以获得最佳的OPT、相对测地误差和最终匹配误差。
这些结果表明,在训练过程中使用多个损失项和修改后的DGCNN可以显著改善匹配结果的质量。
05
结论
提出的神经内在嵌入方法可以有效地解决非刚性点云匹配问题,并且在多个数据集上取得了优于其他方法的结果。该方法可以在不需要额外的先验知识或手动标记的情况下,从点云中提取内在的几何信息,并将其用于点云匹配和分割任务。此外,该方法还具有良好的鲁棒性,可以处理噪声和部分点云等常见的数据伪影。
论文标题:
Neural Intrinsic Embedding for Non-rigid Point Cloud Matching
更多精彩内容请关注公众号:BFT机器人
本文为原创文章,版权归BFT机器人所有,如需转载请与我们联系。若您对该文章内容有任何疑问,请与我们联系,将及时回应。