实践要求

1. 问题描述

各种内部排序算法的时间复杂度分析结果只给出了算法执行时间的阶，或大概执行时间，试通过随机的数据比较各算法的关键字比较次数和关键字移动次数，以取得直观感受。

2. 基本要求

对以下10种常用的内部排序算法进行比较:直接插入排序、折半插入排序、二路插入排序、希尔排序、起泡排序、快速排序、简单选择排序、堆排序、归并排序、基数排序。
待排序表的表长不少于100；其中的数据要用伪随机数产生程序产生；至少要用5组不同的输入数据作比较；比较的指标为有关键字参加的比较次数和关键字的移动次数(关键字交换计为3次移动)。

3. 测试数据

由随机数产生器决定。

4. 实现提示

主要工作是设法在程序中的适当地方插入计数操作。程序还可以包括计算几组数据均值的操作。最后要对结果作出简单分析，包括对各组数据得出结果波动大小的解释。注意分块调试的方法。

实践报告

1. 题目分析

说明程序设计的任务，强调的是程序要做什么，此外列出各成员分工

程序设计任务：
比较十种不同的内排序算法

2. 程序设计

实现概要设计中的数据类型，对主程序、模块及主要操作写出伪代码，画出函数的调用关系

十种内排序算法

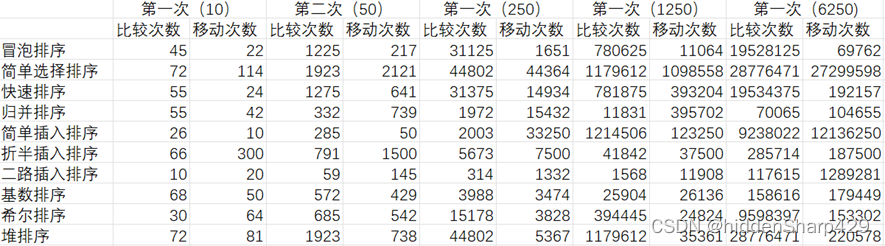
3. 测试结果

列出测试结果，包括输入和输出

在这里插入图片描述

4. 用户使用说明

给出主界面及主要功能界面

无需任何操作，自动测试

5. 附录

源程序文件清单:
sorce.cpp

6. 全部代码

source.cpp

#include <algorithm>
#include <iostream>
#include <random>
#include <vector>
using namespace std;

// 关键字参加的交换次数
long long comparison_times = 0;

// 关键字参加的移动次数
long long move_times = 0;

// 随机数生成器，生成int范围内的整数
std::random_device seed;
std::default_random_engine engine{seed()};
std::uniform_int_distribution<int> dis(INT_MIN, INT_MAX);

// 排序算法 - 冒泡排序,
// 通过相邻元素的比较和交换,在每一轮使一个元素移动到正确的位置。
// 时间复杂度O(n^2)
// 总体来说,选择排序每次交换都是使得最小值移至最前,效率略高一点。冒泡排序每次比较都可能发生交换,效率略低。
void bubbling_sort(vector<int> &arr) {
    for (int i = 0; i < arr.size(); ++i) {
        for (int j = 1; j < arr.size() - i; ++j) {
            ++comparison_times;
            if (arr[j] < arr[j - 1]) {
                swap(arr[j], arr[j - 1]);
                move_times += 3;
            }
        }
    }
}

// 排序算法 - 简单选择排序
// 每一轮从未排序的元素中选出最小的元素,使其移动到已排序的序列的末尾。
// 时间复杂度O(n^2)
void simple_selection_sort(vector<int> &arr) {
    for (int i = 0; i < arr.size(); ++i) {
        ++move_times;
        int min_index = i;
        for (int j = i; j < arr.size(); ++j) {
            ++comparison_times;
            if (arr[min_index] > arr[j]) {
                min_index = j;
                ++move_times;
            }
        }
        swap(arr[min_index], arr[i]);
        move_times += 3;
    }
}

// 排序算法 - 快速排序算法
void quick_sort(vector<int> &arr, int left, int right) {
    // 递归终止条件:区间只有0或1个元素,已然有序,无需继续划分
    if (right - left < 1) {
        return;
    }

    // 随机选取一个数作为基准数Pivot
    int index = left + rand() % (right - left + 1);
    int pivot = arr[index];
    ++move_times;

    // 初始化左右指针lt和gt,cnt用于遍历,lt表示小于pivot的最后一个元素,gt表示大于pivot的第一个元素
    int lt = left;
    int gt = right;
    int cnt = left;

    // 遍历数组,进行三向切分
    while (cnt <= gt) {
        // 当前元素小于pivot,则交换至左指针lt处,lt和cnt同时右移
        ++comparison_times;
        if (arr[cnt] < pivot) {
            swap(arr[cnt++], arr[lt++]);
            move_times += 3;
        }
        // 当前元素大于pivot,则交换至右指针gt处,gt左移
        else if (arr[cnt] > pivot) {
            swap(arr[gt--], arr[cnt]);
            move_times += 3;
        }
        // 等于pivot,直接跳过
        else {
            ++cnt;
        }
    }

    // 递归调用,继续对左右两部分进行快速排序
    quick_sort(arr, left, lt - 1);
    quick_sort(arr, gt + 1, right);
}

// 排序算法 - 归并排序：通过递归将数组划分为两部分,排序后合并得到最终结果。
void merge_sort(vector<int> &tmp, vector<int> &arr, int left, int right) {
    if (right - left < 1) {  // 递归终止条件,子数组长度为 1
        return;
    }
    int mid = left + ((right - left) >> 1);  // 取中间索引
    merge_sort(tmp, arr, left, mid);         // 对左半部分排序
    merge_sort(tmp, arr, mid + 1, right);    // 对右半部分排序

    int l = left, r = mid + 1, k = 0;  // 初始化变量
    while (l <= left && r <= right) {  // 双指针,取较小者
        ++comparison_times;
        ++move_times;
        if (arr[l] < arr[r]) {
            tmp[k++] = arr[l++];  // 将较小值放入 tmp,指针后移
        } else {
            tmp[k++] = arr[r++];
        }
    }
    while (l <= mid) {  // 将左半部分剩余元素放入 tmp
        ++move_times;
        tmp[k++] = arr[l++];
    }
    while (r <= right) {  // 将右半部分剩余元素放入 tmp
        ++move_times;
        tmp[k++] = arr[r++];
    }
    copy(tmp.begin(), tmp.begin() + (right - left + 1),
         arr.begin() + left);  // 将 tmp 拷贝回 arr
    move_times += right - left + 1;
}

// 排序算法 - 简单插入排序
void simple_insertion_sort(vector<int> &arr) {
    for (int i = 1; i < arr.size(); ++i) {
        for (int j = i - 1; j >= 0; --j) {
            ++comparison_times;
            if (arr[j + 1] < arr[j]) {
                move_times += 3;
                swap(arr[j + 1], arr[j]);
            } else {
                break;
            }
        }
    }
}

// 排序算法 - 折半插入排序
void half_insert_sort(vector<int> &arr) {
    for (int i = 1; i < arr.size(); ++i) {
        int left = 0;
        int right = i - 1;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            ++comparison_times;
            if (arr[mid] > arr[i]) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        for (int k = i; k >= left; --k) {
            swap(arr[left], arr[k]);
            move_times += 3;
        }
    }
}

// 排序算法 - 二路插入排序
// 将数组分成已排序和未排序两部分,每次从未排序的部分找一个最小的元素插入到已排序的部分中。
// 时间复杂度O(n^2)
void two_way_insertion_sort(vector<int> &arr) {
    for (int i = 1; i < arr.size(); ++i) {
        ++move_times;
        int key = arr[i];
        int j = i - 1;
        // 找到已排序部分第一个大于等于key的元素,并记录其索引
        while (j >= 0 && arr[j] > key && (++comparison_times)) {
            ++move_times;
            arr[j + 1] = arr[j];
            j--;
        }
        // 在已排序部分的正确位置插入key
        arr[j + 1] = key;
        ++move_times;
    }
}

// 排序算法 - 基数排序
// 针对每一位数进行排序,从低位到高位逐渐排序,实现整体有序。要求元素的表示形式从低位到高位是有意义的。
// 时间复杂度O(n*k),其中k是排序位数。
void radix_sort(vector<int> &arr) {
    // 获取最大数,确定排序位数
    int max_num = *max_element(arr.begin(), arr.end());
    comparison_times += arr.size();

    int num_digits = 0;
    while (max_num > 0) {
        max_num /= 10;
        num_digits++;
    }

    // 设置10个桶
    vector<vector<int>> buckets(10);
    // 按位排序,从个位开始
    for (int pos = 0; pos < num_digits; pos++) {
        // 将所有整数按指定位数放入桶中
        for (int num : arr) {
            int digit = 0;
            buckets[digit].push_back(num);
            ++move_times;
        }

        // 按桶顺序输出
        move_times += arr.size();
        arr.clear();

        for (auto &bucket : buckets) {
            for (int num : bucket) {
                ++move_times;
                arr.push_back(num);
            }
            bucket.clear();
        }
    }
}

// 排序算法 - 希尔排序
// 是插入排序的一种优化版本。它通过间隔为h的增量来比较并交换相隔h个元素,采用递减的h值,最终当h=1时,变成普通的插入排序。
// 时间复杂度O(nlogn)
void shell_sort(vector<int> &arr) {
    int h = 1;
    while (h < arr.size() / 3) {
        h = 3 * h + 1;  // 确定初始步长h
    }

    while (h >= 1) {
        for (int i = h; i < arr.size(); i++) {
            int j = i;
            int temp = arr[i];
            ++move_times;
            while (j >= h && arr[j - h] > temp && ++comparison_times) {
                ++move_times;
                arr[j] = arr[j - h];
                j -= h;
            }
            ++move_times;
            arr[j] = temp;
        }
        h /= 3;  // 步长缩小
    }
}

// 排序算法 - 堆排序,利用堆结构(可看成完全二叉树)的特点实现排序。
// 时间复杂度O(nlogn)
void heapify(vector<int> &arr, int n, int i) {
    int largest = i;    // 目前最大值的索引
    int l = 2 * i + 1;  // 左子节点索引
    int r = 2 * i + 2;  // 右子节点索引

    comparison_times += 2;
    if (l < n && arr[l] > arr[largest]) largest = l;
    if (r < n && arr[r] > arr[largest]) largest = r;
    if (largest != i) {
        swap(arr[i], arr[largest]);
        move_times += 3;
        heapify(arr, n, largest);
    }
}

void heap_sort(vector<int> &arr) {
    // 建立最大堆,将数组转换成最大堆
    for (int i = arr.size() / 2 - 1; i >= 0; i--) heapify(arr, arr.size(), i);

    // 交换根节点和最后一个节点,调整最大堆,重复此操作
    for (int i = arr.size() - 1; i >= 0; i--) {
        move_times += 3;
        swap(arr[0], arr[i]);
        heapify(arr, i, 0);
    }
}

void restore_status(vector<int> &tmp, vector<int> &arr,
                    long long &comparison_times, long long &move_times) {
    tmp = arr;
    comparison_times = 0;
    move_times = 0;
    return;
}

void print_statistical_results(const long long &comparison_times,
                               const long long &move_times) {
    cout << comparison_times << ' ' << move_times << '\n';
}

int main() {
    // ios::sync_with_stdio(false);
    int step = 10;
    for (int i = 0; i < 5; ++i, step *= 5) {
        vector<int> arr, tmp;
        for (int j = 0; j < step; ++j) {
            arr.push_back(dis(engine));
        }

        // 冒泡排序
        restore_status(tmp, arr, comparison_times, move_times);
        bubbling_sort(tmp);
        print_statistical_results(comparison_times, move_times);

        // 简单选择排序
        restore_status(tmp, arr, comparison_times, move_times);
        simple_selection_sort(tmp);
        print_statistical_results(comparison_times, move_times);

        // 快速排序
        restore_status(tmp, arr, comparison_times, move_times);
        quick_sort(tmp, 0, tmp.size() - 1);
        print_statistical_results(comparison_times, move_times);

        // 归并排序
        restore_status(tmp, arr, comparison_times, move_times);
        vector<int> temporary(arr.size());
        merge_sort(temporary, tmp, 0, arr.size() - 1);
        print_statistical_results(comparison_times, move_times);

        // 简单插入排序
        restore_status(tmp, arr, comparison_times, move_times);
        simple_insertion_sort(tmp);
        print_statistical_results(comparison_times, move_times);

        // 折半插入排序
        restore_status(tmp, arr, comparison_times, move_times);
        half_insert_sort(tmp);
        print_statistical_results(comparison_times, move_times);

        // 二路插入排序
        restore_status(tmp, arr, comparison_times, move_times);
        two_way_insertion_sort(tmp);
        print_statistical_results(comparison_times, move_times);

        // 基数排序
        restore_status(tmp, arr, comparison_times, move_times);
        radix_sort(tmp);
        print_statistical_results(comparison_times, move_times);

        // 希尔排序
        restore_status(tmp, arr, comparison_times, move_times);
        shell_sort(tmp);
        print_statistical_results(comparison_times, move_times);

        // 堆排序
        restore_status(tmp, arr, comparison_times, move_times);
        heap_sort(tmp);
        print_statistical_results(comparison_times, move_times);

        cout << endl;
    }
    cout << "end";
    return 0;
}