穷举法Exhaustive method是使用最广泛、设计最简单,同时最耗时的算法,也被称为暴力法、蛮力法Brute force method。
两数之和
给定一个整数数组array和一个目标值target,请在数组中找出和为目标值target的两个整数,并输出它们在数组array中的下标。
我们可以通过如下代码尝试解决:
#include<iostream>
//数组指针,数组元素个数,目标值
void outputIndexOfArray(int* array, int length, int target) {
bool result = false;
for (int index_1 = 0; index_1 < length; index_1++) {
for (int index_2 = 0; index_2 < length; index_2++) {
if (index_1 != index_2 && array[index_1] + array[index_2] == target) {
std::cout << "array[" << index_1 << "]+array[" << index_2 << "]=" << target << std::endl;
result = true;
}
}
}
if (!result) {
std::cout << "无解" << std::endl;
}
}
int main() {
int array[10];
for (int i = 0; i < 10; i++) {
array[i] = i;
}
outputIndexOfArray(array, sizeof(array) / sizeof(array[0]), 10);
}
这个代码不难理解,需要注意的是:
C++中函数参数为数组时,函数内无法使用sizeof(array)/sizeof(array[0])的方法获取数组长度,这种方法得到的是指针大小/元素大小。
需要额外的参数来传递数组大小。
运行之后我们会发现第一个结果和最后一个结果是相同的,空间中存在重复的解。
将这个题的解集用二维数组表示,就能看出问题所在。
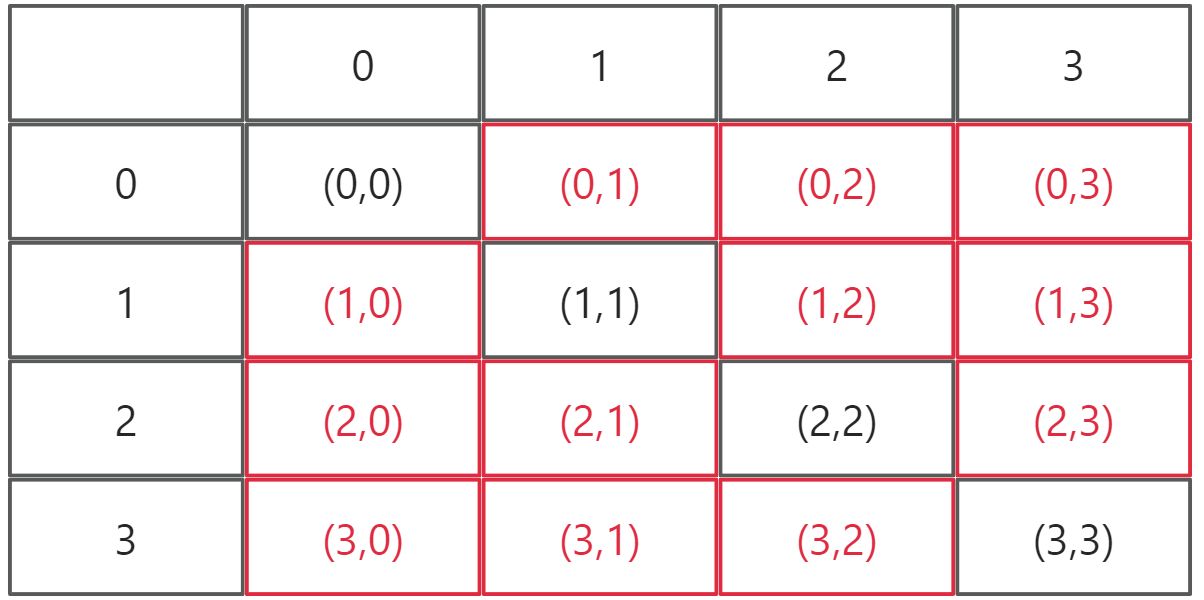
这是一个角对称矩阵,矩阵中(i,j)和(j,i)表示的组合是等价的。
我们将本题的解空间缩小到这个矩阵的上对角矩阵或下对角矩阵(不包含对角线),这样得到的结果就不会有重复了。
在代码实现上,只要将内层循环变量index_2的起始值从原来的0改为index_1+1,就可以将搜索范围限定到上对角矩阵,解空间就变为原来的一半,同时不再需要index_1!=index_2的判断。
改进后的算法实现如下:
#include<iostream>
//数组指针,数组元素个数,目标值
void outputIndexOfArray(int* array, int length, int target) {
bool result = false;
for (int index_1 = 0; index_1 < length; index_1++) {
for (int index_2 = index_1 + 1; index_2 < length; index_2++) {
if (array[index_1] + array[index_2] == target) {
std::cout << "array[" << index_1 << "]+array[" << index_2 << "]=" << target << std::endl;
result = true;
}
}
}
if (!result) {
std::cout << "无解" << std::endl;
}
}
int main() {
int array[10];
for (int i = 0; i < 10; i++) {
array[i] = i;
}
outputIndexOfArray(array, sizeof(array) / sizeof(array[0]), 10);
}
压缩了问题的解空间后,之前的重复结果被消除,运行结果符合预期。
在应用穷举法解决问题时,关键是划定好问题的解空间。如果解空间的范围定得过大,那么不但会增加冗余的搜索操作,还可能导致结果重复;如果解空间的范围定得过小,则可能漏掉一部分解,违背了穷举法牺牲时间换取解的全面性的初衷。
百钱百鸡
我国古代数学家张丘建在《算经》一书中提出了著名的“百钱百鸡”问题:
鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一。百钱买百鸡,则翁、母、雏各几何?
可将问题抽象成以下方程组:
{
5
x
+
3
y
+
1
3
z
=
100
x
+
y
+
z
=
100
\begin{cases} 5x+3y+\frac{1}{3}z=100\\ x+y+z=100 \end{cases}
{5x+3y+31z=100x+y+z=100
该方程组中包含三个未知数,仅有两个方程,是一个三元一次不定方程组。根据代数基本定理,该方程组会有无数组解,但是本题存在约束条件,所以它的解是一定有限的。
由于整型在计算时会自动舍弃小数部分,这样会造成误差,从而影响最终的结果,我们需要对第一个方程两边同时乘上三。
#include<iostream>
void buyChicken() {
for (int x = 0; x <= 100; x++) {
for (int y = 0; y <= 100; y++) {
for (int z = 0; z <= 100; z++) {
if (x + y + z == 100 && 15 * x + 9 * y + z == 300) {
std::cout << "cock:" << x << "hen:" << y << "chick:" << z << std::endl;
}
}
}
}
}
int main() {
buyChicken();
}
Meziak的砝码问题
一位商人有一个质量为40磅的砝码,一天,他不小心将这个砝码摔成了4块。吝啬的商人不愿意扔掉这个破碎的砝码,于是他仔细研究这4块砝码碎片,发现恰好每块砝码碎片的质量都是整数,而且各不相同,同时这4块砝码碎片可以在天平上称出1-40磅的任意整数磅。求出这4块砝码碎片的质量各是多少。
从题目给出的已知条件,我们可以总结出以下几点:
- 四块砝码碎片的质量都是整数,并且质量之和为10磅。
- 砝码碎片的质量各不相同。
- 四块砝码碎片可以在天平上称出
1~40磅任意整数磅的质量。
所以这个问题的解空间是有限的、可列的。我们只需要划定一个合理的解空间,并在这个解空间中搜索出满足以上三个条件的解。
消除冗余解
与两数之和问题一样,组合(1,2,3,4)和(4,3,2,1)是等价的,所以只需要考虑碎片的质量各是多少,不需要考虑碎片的排列方式。我们需要划定一个不重、不漏的解空间。
“两数之和”问题的解空间是一个二维矩阵,而本题的解空间是一个四维向量,可将上面的算法类比推广到思维向量解空间的问题上:
void MeziakWeight() {
int a, b, c, d;
for (a = 1; a < 40; a++) {
for (b = a + 1; b < 40; b++) {
for (c = b + 1; c < 40; c++) {
for (d = c + 1; d < 40; d++) {
//是否质量之和等于40
//是否可以称出1~40任意整数磅的质量
}
}
}
}
}
这里将内层循环的变量b、c、d的起点从原来的1改为上一层循环变量值加1,这样既可以清除解空间中的冗余解,又可以在判断结果时省略对“砝码碎片的质量各不相同”这一条件的判断,因为循环的最内层得到的abcd一定不相等。
任意整数磅
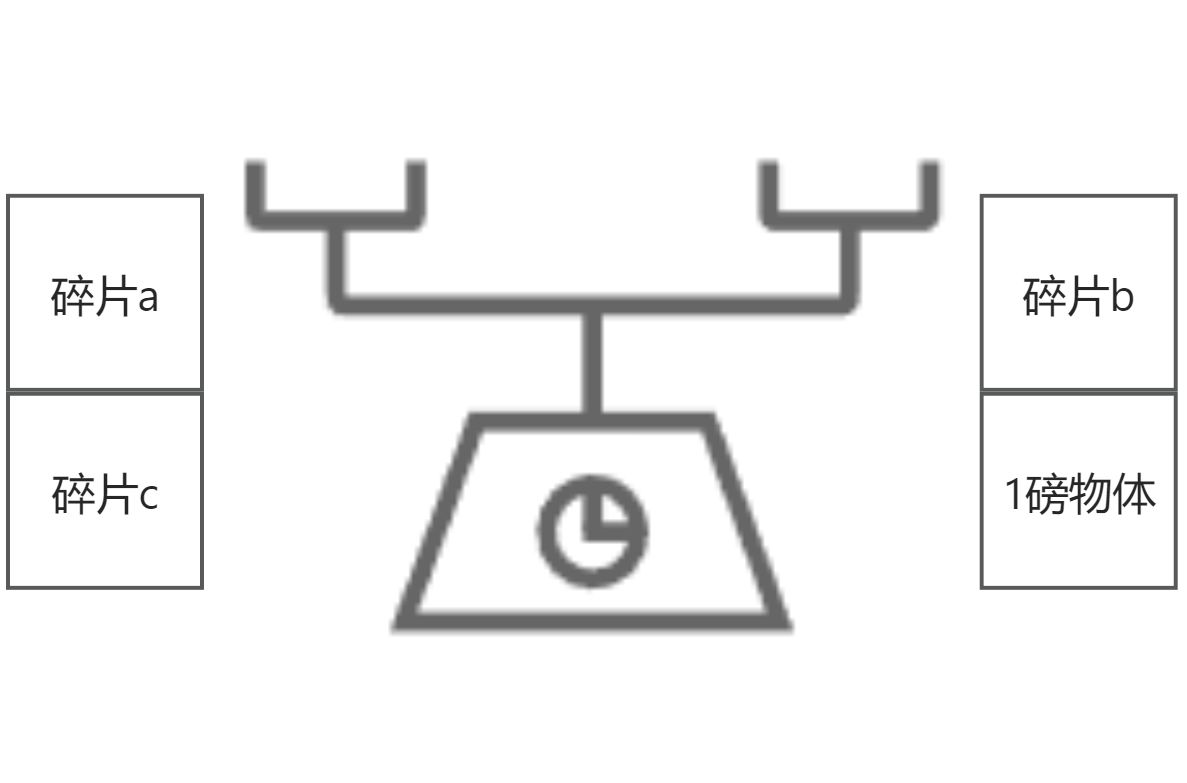
将碎片a和碎片c放到天平的一边,将碎片b和一个1磅的苹果放到天平的另一边,此时天平保持平衡。这说明砝码abc可以称出1磅的质量,我们可以通过交换砝码碎片的组合和摆放位置来称出不同的质量。
如果将这个问题转化为数学符号,其实就是判断方程在W=1,2…40时是否都有解:
x
1
a
+
x
2
b
+
x
3
c
+
x
4
d
=
W
x
1
,
x
2
,
x
3
,
x
4
∈
{
x
1
,
x
2
,
x
3
,
x
4
}
x_1a+x_2b+x_3c+x_4d=W\quad x_1,x_2,x_3,x_4\in\left\{x_1,x_2,x_3,x_4\right\}
x1a+x2b+x3c+x4d=Wx1,x2,x3,x4∈{x1,x2,x3,x4}
代码实现如下:
bool isMeasurableOneToForty(int a, int b, int c, int d) {
int weight;
for (weight = 1; weight <= 40; weight++) {
if (!isMeasurable(a, b, c, d, weight)) {
return false;
}
}
return true;
}
bool isMeasurable(int a, int b, int c, int d, int weight) {
int x1, x2, x3, x4;
for (x1 = -1; x1 <= 1; x1++) {
for (x2 = -1; x2 <= 1; x2++) {
for (x3 = -1; x3 <= 1; x3++) {
for (x4 = -1; x4 <= 1; x4++) {
if (x1 * a + x2 * b + x3 * c + x4 * d == weight)
return true;
}
}
}
}
return false;
}
在函数isMeasurableOneToForty()中,通过一个循环语句来判断砝码碎片组合abcd是否可以称出1~40的任意整数磅。如果可以则返回true,否则返回false。
函数isMeasurable()包含5个参数。如果碎片组合abcd能称出weight所表示的质量,则函数isMeasurable()返回true,否则返回false。
#include<iostream>
bool isMeasurable(int a, int b, int c, int d, int weight);
bool isMeasurableOneToForty(int a, int b, int c, int d);
void MeziakWeight();
int main() {
MeziakWeight();
}
void MeziakWeight() {
int a, b, c, d;
for (a = 1; a < 40; a++) {
for (b = a + 1; b < 40; b++) {
for (c = b + 1; c < 40; c++) {
for (d = c + 1; d < 40; d++) {
if (a + b + c + d == 40 && isMeasurableOneToForty(a, b, c, d)) {
std::cout << a << " " << b << " " << c << " " << d << std::endl;
}
}
}
}
}
}
bool isMeasurableOneToForty(int a, int b, int c, int d) {
int weight;
for (weight = 1; weight <= 40; weight++) {
if (!isMeasurable(a, b, c, d, weight)) {
return false;
}
}
return true;
}
bool isMeasurable(int a, int b, int c, int d, int weight) {
int x1, x2, x3, x4;
for (x1 = -1; x1 <= 1; x1++) {
for (x2 = -1; x2 <= 1; x2++) {
for (x3 = -1; x3 <= 1; x3++) {
for (x4 = -1; x4 <= 1; x4++) {
if (x1 * a + x2 * b + x3 * c + x4 * d == weight)
return true;
}
}
}
}
return false;
}
总结
牺牲时间换取解的全面性。
上面的三个问题都可以化为对整数解的方程组求解的问题。
求解的过程就是对范围内的所有可能值进行尝试。
尝试的时候需要注意重复解的问题。对于那些不限定顺序的题目,内层循环的计数器起始值可以尝试从+1开始。
起始值从0开始还是从1开始,到哪里结束,要看实际问题,要看我们要遍历的是什么。
在排序算法中,我们如果遍历的是下标,那就是从0开始,循环条件就是<=size-1。
如果遍历的是下标,那就是从1开始,循环条件就是<=size。
在砝码中,解方程时,我们要对变量可能的系数逐一尝试,因此遍历的范围就是[-1,1]。
在穷举的时候,要特别注意是否存在重复、如何处理重复的问题以及我遍历的到底是什么的问题。