目录
1. 什么是哈夫曼树
2. 为什么有哈夫曼树
3. 哈夫曼树的原理
3.1 哈夫曼树的构造方法
3.2 哈夫曼解码
3.3 几种定义
4. 哈夫曼二叉树的特点
5. 关于哈夫曼树的代码
1. 什么是哈夫曼树
- 哈夫曼树解决的是编码问题,给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。说的直白一点就是找出存放一串字符所需的最少的二进制编码。
2. 为什么有哈夫曼树
- 如下图:我们存到T(S)里的编码比较长,比较繁琐,有没有一种更简洁的方法呢?

3. 哈夫曼树的原理
3.1 哈夫曼树的构造方法
- 可以用下面的方法:首先标出每个元素出现的次数

- 第一步:找出字符中最小的两个,小的在左边,大的在右边,组成二叉树。在频率表中删除此次找到的两个数,并加入此次最小两个数的频率和,下列E和D最小组成一个二叉树。

- 第二步:以此类推,再找出字符中最小的两个,小的在左边,大的在右边,组成二叉树。
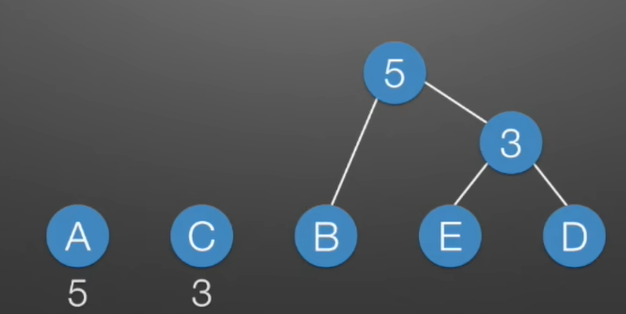

第三步:我们给每个左分支标记为0,给每个右分支标记为1
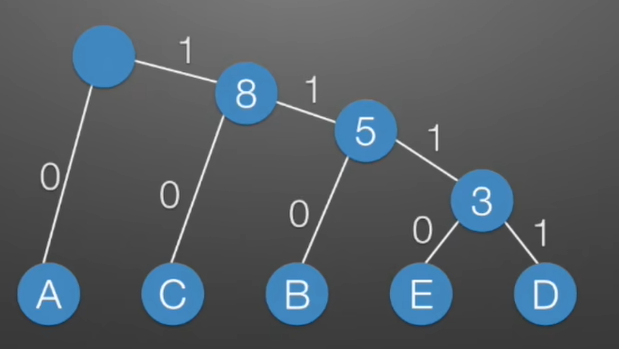
- 第四步:每个 字符 的 二进制编码 为(从根节点数到对应的叶子节点,路径上的值拼接起来就是叶子节点字母的应该的编码)

- 现在生成的H(S)是不是比T(S)短了不少

3.2 哈夫曼解码
- 从左向右扫描二叉树,当到了叶子节点时候输出原始值。
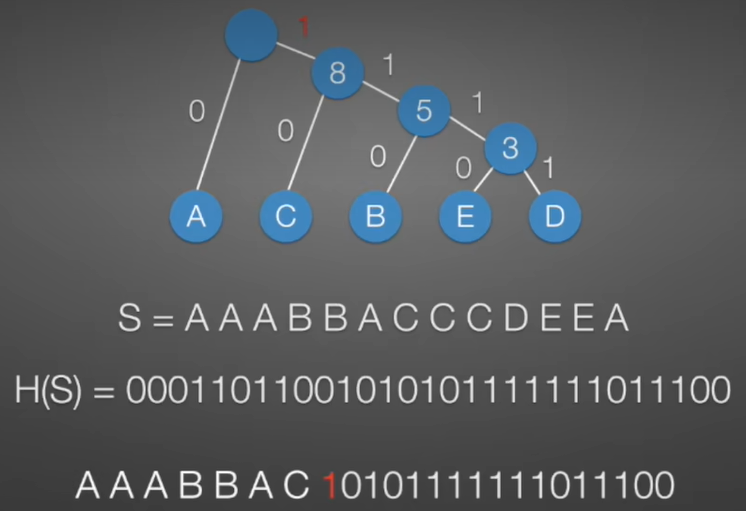
问题:会不会出现长编码的不与短编码的字母冲突:答案是不会的,因为扫描二叉树都是每次扫描到叶子节点,不会出现返回的现象。

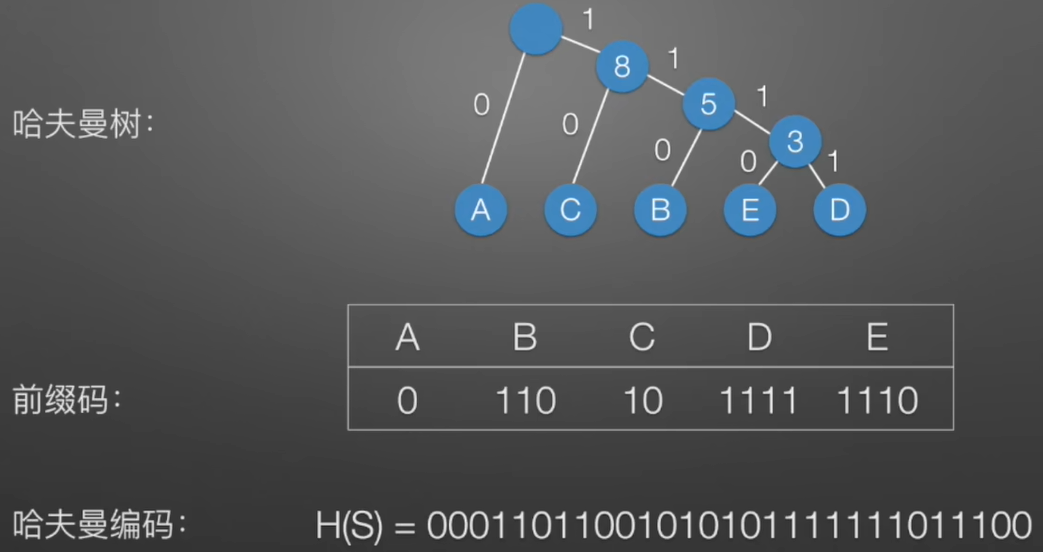
3.3 几种定义
- 路径:路径是指从树中一个结点到另一个结点的分支所构成的路线。
- 树的路径长度:树的路径长度是指从根到每个结点的路径长度之和。
- 带权路径长度:结点具有权值,从该结点到根之间的路径长度乘以结点的权值,就是该结点的带权路径长度。如:E的带权路径长度=4x2=8
- 树的带权路径长度(WPL):树的带权路径长度(WPL) 是指树中所有叶子结点的带权路径长度之和。如:WPL =1x5 + 3x2 + 2x3 +2x4 + 1x4 =29
4. 哈夫曼二叉树的特点
- 权值越大的结点,距离根结点越近。
- 树中没有度为1的结点。这类树又叫作正则严格)二叉树。
- 树的带权路径长度最短。
5. 关于哈夫曼树的代码
typedef char **HuffmanCode;
//生成哈夫曼编码
void HuffCoding(HuffmanTree& HT, HuffmanCode& HC, int n)
{
HC = (HuffmanCode)malloc(sizeof(char*)*(n + 1)); //开n+1个空间,因为下标为0的空间不用
char* code = (char*)malloc(sizeof(char)*n); //辅助空间,编码最长为n(最长时,前n-1个用于存储数据,最后1个用于存放'\0')
code[n - 1] = '\0'; //辅助空间最后一个位置为'\0'
for (int i = 1; i <= n; i++)
{
int start = n - 1; //每次生成数据的哈夫曼编码之前,先将start指针指向'\0'
int c = i; //正在进行的第i个数据的编码
int p = HT[c].parent; //找到该数据的父结点
while (p) //直到父结点为0,即父结点为根结点时,停止
{
if (HT[p].lc == c) //如果该结点是其父结点的左孩子,则编码为0,否则为1
code[--start] = '0';
else
code[--start] = '1';
c = p; //继续往上进行编码
p = HT[c].parent; //c的父结点
}
HC[i] = (char*)malloc(sizeof(char)*(n - start)); //开辟用于存储编码的内存空间
strcpy(HC[i], &code[start]); //将编码拷贝到字符指针数组中的相应位置
}
free(code); //释放辅助空间
}
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef double DataType; //结点权值的数据类型
typedef struct HTNode //单个结点的信息
{
DataType weight; //权值
int parent; //父节点
int lc, rc; //左右孩子
}*HuffmanTree;
typedef char **HuffmanCode; //字符指针数组中存储的元素类型
//在下标为1到i-1的范围找到权值最小的两个值的下标,其中s1的权值小于s2的权值
void Select(HuffmanTree& HT, int n, int& s1, int& s2)
{
int min;
//找第一个最小值
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0)
{
min = i;
break;
}
}
for (int i = min + 1; i <= n; i++)
{
if (HT[i].parent == 0 && HT[i].weight < HT[min].weight)
min = i;
}
s1 = min; //第一个最小值给s1
//找第二个最小值
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0 && i != s1)
{
min = i;
break;
}
}
for (int i = min + 1; i <= n; i++)
{
if (HT[i].parent == 0 && HT[i].weight < HT[min].weight&&i != s1)
min = i;
}
s2 = min; //第二个最小值给s2
}
//构建哈夫曼树
void CreateHuff(HuffmanTree& HT, DataType* w, int n)
{
int m = 2 * n - 1; //哈夫曼树总结点数
HT = (HuffmanTree)calloc(m + 1, sizeof(HTNode)); //开m+1个HTNode,因为下标为0的HTNode不存储数据
for (int i = 1; i <= n; i++)
{
HT[i].weight = w[i - 1]; //赋权值给n个叶子结点
}
for (int i = n + 1; i <= m; i++) //构建哈夫曼树
{
//选择权值最小的s1和s2,生成它们的父结点
int s1, s2;
Select(HT, i - 1, s1, s2); //在下标为1到i-1的范围找到权值最小的两个值的下标,其中s1的权值小于s2的权值
HT[i].weight = HT[s1].weight + HT[s2].weight; //i的权重是s1和s2的权重之和
HT[s1].parent = i; //s1的父亲是i
HT[s2].parent = i; //s2的父亲是i
HT[i].lc = s1; //左孩子是s1
HT[i].rc = s2; //右孩子是s2
}
//打印哈夫曼树中各结点之间的关系
printf("哈夫曼树为:>\n");
printf("下标 权值 父结点 左孩子 右孩子\n");
printf("0 \n");
for (int i = 1; i <= m; i++)
{
printf("%-4d %-6.2lf %-6d %-6d %-6d\n", i, HT[i].weight, HT[i].parent, HT[i].lc, HT[i].rc);
}
printf("\n");
}
//生成哈夫曼编码
void HuffCoding(HuffmanTree& HT, HuffmanCode& HC, int n)
{
HC = (HuffmanCode)malloc(sizeof(char*)*(n + 1)); //开n+1个空间,因为下标为0的空间不用
char* code = (char*)malloc(sizeof(char)*n); //辅助空间,编码最长为n(最长时,前n-1个用于存储数据,最后1个用于存放'\0')
code[n - 1] = '\0'; //辅助空间最后一个位置为'\0'
for (int i = 1; i <= n; i++)
{
int start = n - 1; //每次生成数据的哈夫曼编码之前,先将start指针指向'\0'
int c = i; //正在进行的第i个数据的编码
int p = HT[c].parent; //找到该数据的父结点
while (p) //直到父结点为0,即父结点为根结点时,停止
{
if (HT[p].lc == c) //如果该结点是其父结点的左孩子,则编码为0,否则为1
code[--start] = '0';
else
code[--start] = '1';
c = p; //继续往上进行编码
p = HT[c].parent; //c的父结点
}
HC[i] = (char*)malloc(sizeof(char)*(n - start)); //开辟用于存储编码的内存空间
strcpy(HC[i], &code[start]); //将编码拷贝到字符指针数组中的相应位置
}
free(code); //释放辅助空间
}
//主函数
int main()
{
int n = 0;
printf("请输入数据个数:>");
scanf("%d", &n);
DataType* w = (DataType*)malloc(sizeof(DataType)*n);
if (w == NULL)
{
printf("malloc fail\n");
exit(-1);
}
printf("请输入数据:>");
for (int i = 0; i < n; i++)
{
scanf("%lf", &w[i]);
}
HuffmanTree HT;
CreateHuff(HT, w, n); //构建哈夫曼树
HuffmanCode HC;
HuffCoding(HT, HC, n); //构建哈夫曼编码
for (int i = 1; i <= n; i++) //打印哈夫曼编码
{
printf("数据%.2lf的编码为:%s\n", HT[i].weight, HC[i]);
}
free(w);
return 0;
}