题目及测试
package pid060;
/* 60. 排列序列
给出集合 [1,2,3,...,n],其所有元素共有 n! 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:
"123"
"132"
"213"
"231"
"312"
"321"
给定 n 和 k,返回第 k 个排列。
示例 1:
输入:n = 3, k = 3
输出:"213"
示例 2:
输入:n = 4, k = 9
输出:"2314"
示例 3:
输入:n = 3, k = 1
输出:"123"
提示:
1 <= n <= 9
1 <= k <= n!
*/
import java.util.List;
public class main {
public static void main(String[] args) {
int [] testTable = {3,4,3};
int [] testTable2 = {3,9,1};
for(int i=0;i<testTable.length;i++){
test(testTable[i],testTable2[i]);
}
}
private static void test(int ito,int ito2) {
Solution solution = new Solution();
String rtn;
long begin = System.currentTimeMillis();
System.out.print(ito+" ");
System.out.print(ito2);
System.out.println();
//开始时打印数组
rtn= solution.getPermutation(ito,ito2);//执行程序
long end = System.currentTimeMillis();
System.out.println("rtn=" );
System.out.print(rtn);
System.out.println();
System.out.println("耗时:" + (end - begin) + "ms");
System.out.println("-------------------");
}
}
没想出来
解法1(别人的)
一句话题解:以下给出了两种方法,思路其实是一样的:通过 计算剩余数字个数的阶乘数,一位一位选出第 k 个排列的数位。
思路分析:容易想到,使用同「力扣」第 46 题: 全排列 的回溯搜索算法,依次得到全排列,输出第 k 个全排列即可。事实上,我们不必求出所有的全排列。
基于以下几点考虑:
所求排列 一定在叶子结点处得到,进入每一个分支,可以根据已经选定的数的个数,进而计算还未选定的数的个数,然后计算阶乘,就知道这一个分支的 叶子结点 的个数:
如果 k 大于这一个分支将要产生的叶子结点数,直接跳过这个分支,这个操作叫「剪枝」;
如果 k 小于等于这一个分支将要产生的叶子结点数,那说明所求的全排列一定在这一个分支将要产生的叶子结点里,需要递归求解。

编码注意事项:
计算阶乘的时候,可以使用循环计算。注意:0!=1,它表示了没有数可选的时候,即表示到达叶子结点了,排列数只剩下 1 个;
题目中说「给定 n 的范围是 [1, 9]」,可以把从 0 到 9 的阶乘计算好,放在一个数组里,可以根据索引直接获得阶乘值;编码的时候,+1 还是 −1 ,大于还是大于等于,这些不能靠猜。常见的做法是:代入一个具体的数值,认真调试。
回溯搜索算法 + 剪枝 ,直接来到叶子结点
import java.util.Arrays;
public class Solution {
/**
* 记录数字是否使用过
*/
private boolean[] used;
/**
* 阶乘数组
*/
private int[] factorial;
private int n;
private int k;
public String getPermutation(int n, int k) {
this.n = n;
this.k = k;
calculateFactorial(n);
// 查找全排列需要的布尔数组
used = new boolean[n + 1];
Arrays.fill(used, false);
StringBuilder path = new StringBuilder();
dfs(0, path);
return path.toString();
}
/**
* @param index 在这一步之前已经选择了几个数字,其值恰好等于这一步需要确定的下标位置
* @param path
*/
private void dfs(int index, StringBuilder path) {
if (index == n) {
return;
}
// 计算还未确定的数字的全排列的个数,第 1 次进入的时候是 n - 1
int cnt = factorial[n - 1 - index];
for (int i = 1; i <= n; i++) {
if (used[i]) {
continue;
}
if (cnt < k) {
k -= cnt;
continue;
}
path.append(i);
used[i] = true;
dfs(index + 1, path);
// 注意 1:不可以回溯(重置变量),算法设计是「一下子来到叶子结点」,没有回头的过程
// 注意 2:这里要加 return,后面的数没有必要遍历去尝试了
return;
}
}
/**
* 计算阶乘数组
*
* @param n
*/
private void calculateFactorial(int n) {
factorial = new int[n + 1];
factorial[0] = 1;
for (int i = 1; i <= n; i++) {
factorial[i] = factorial[i - 1] * i;
}
}
}k -= cnt; 这一步,每一次剪枝太慢,事实上,可以用除法加快这一步骤。但是需要维护一个有序数组(或者链表),时间复杂度不变。
解法2(别人的)
有序数组(链表)模拟
思路分析:以 n = 4,k = 6,为例,现在确定第 1 个数字填啥。如果第 k 个数恰好是后面的数字个数的阶乘,那么第 1 个数字就只能填最小的 1。
如果 n = 4,k = 16,现在确定第 11 个数字填啥。如果 k > 后面的数字个数的阶乘。数一数,可以跳过几个阶乘数。
其实这个思路很像方法一的「剪枝」,只不过方法一就减法,方法二用除法。事实上,方法二要维护数组的有序性,所以时间复杂度不变。根据以上思路,设计算法流程如下:
算法流程设计:
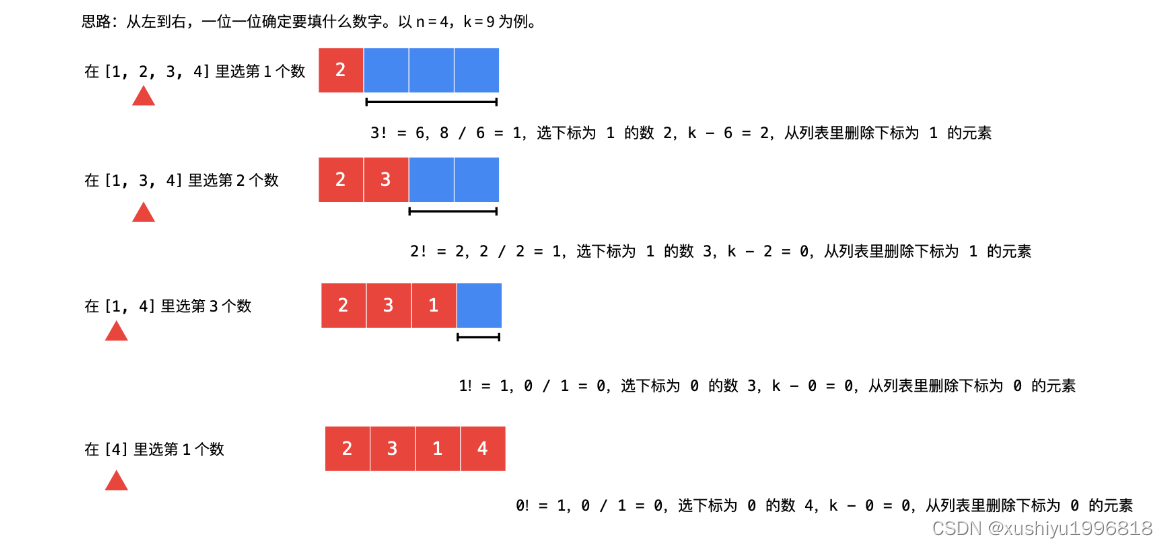
把候选数放在一个 有序列表 里,从左到右根据「剩下的数的阶乘数」确定每一位填谁,公式 k / (后面几位的阶乘数) 的值 恰好等于候选数组的下标;
选出一个数以后,k 就需要减去相应跳过的阶乘数的倍数;
已经填好的数需要从候选列表里删除,注意保持列表的有序性(因为排列的定义是按照字典序);
由于这里考虑的是下标,第 k 个数,下标为 k - 1,一开始的时候,k--。
每次选出一个数,就将这个数从列表里面拿出。这个列表需要支持频繁的删除操作,因此使用双链表。在 Java 中 LinkedList 就是使用双链表实现的。
public class Solution {
public String getPermutation(int n, int k) {
// 注意:相当于在 n 个数字的全排列中找到下标为 k - 1 的那个数,因此 k 先减 1
k --;
int[] factorial = new int[n];
factorial[0] = 1;
// 先算出所有的阶乘值
for (int i = 1; i < n; i++) {
factorial[i] = factorial[i - 1] * i;
}
// 这里使用数组或者链表都行
List<Integer> nums = new LinkedList<>();
for (int i = 1; i <= n; i++) {
nums.add(i);
}
StringBuilder stringBuilder = new StringBuilder();
// i 表示剩余的数字个数,初始化为 n - 1
for (int i = n - 1; i >= 0; i--) {
int index = k / factorial[i] ;
stringBuilder.append(nums.remove(index));
k -= index * factorial[i];
}
return stringBuilder.toString();
}
}