枚举满足条件的左端点能延续的最长右端点

class Solution {
public:
    int longestAlternatingSubarray(vector<int> &nums, int threshold) {
        int res = 0;
        int n = nums.size();
        for (int i = 0; i < n;) {
            if (nums[i] % 2 == 0 && nums[i] <= threshold) {
                int j = i + 1;
                while (j < n && nums[j] <= threshold && nums[j] % 2 != nums[j - 1] % 2)
                    j++;
                res = max(res, j - i);
                i = j;
            } else
                i++;
        }
        return res;
    }
};

线性筛: 预处理求出1~n中的各数是否是质数, 然后枚举x

class Solution {
public:
    vector<vector<int>> findPrimePairs(int n) {
        vector<int> pri;
        vector<int> vis(n + 1);
        for (int i = 2; i <= n; i++) {
            if (!vis[i])//vis[i]==0且i!=1 则i为质数
                pri.push_back(i);
            for (auto pi: pri) {
                if (pi * i > n)
                    break;
                vis[pi * i] = 1;
                if (i % pi == 0)
                    break;
            }
        }
        vector<vector<int>> res;
        for (int i = 2; i <= n - i; i++)
            if (!vis[i] && !vis[n - i])
                res.push_back({i, n - i});
        return res;
    }
};

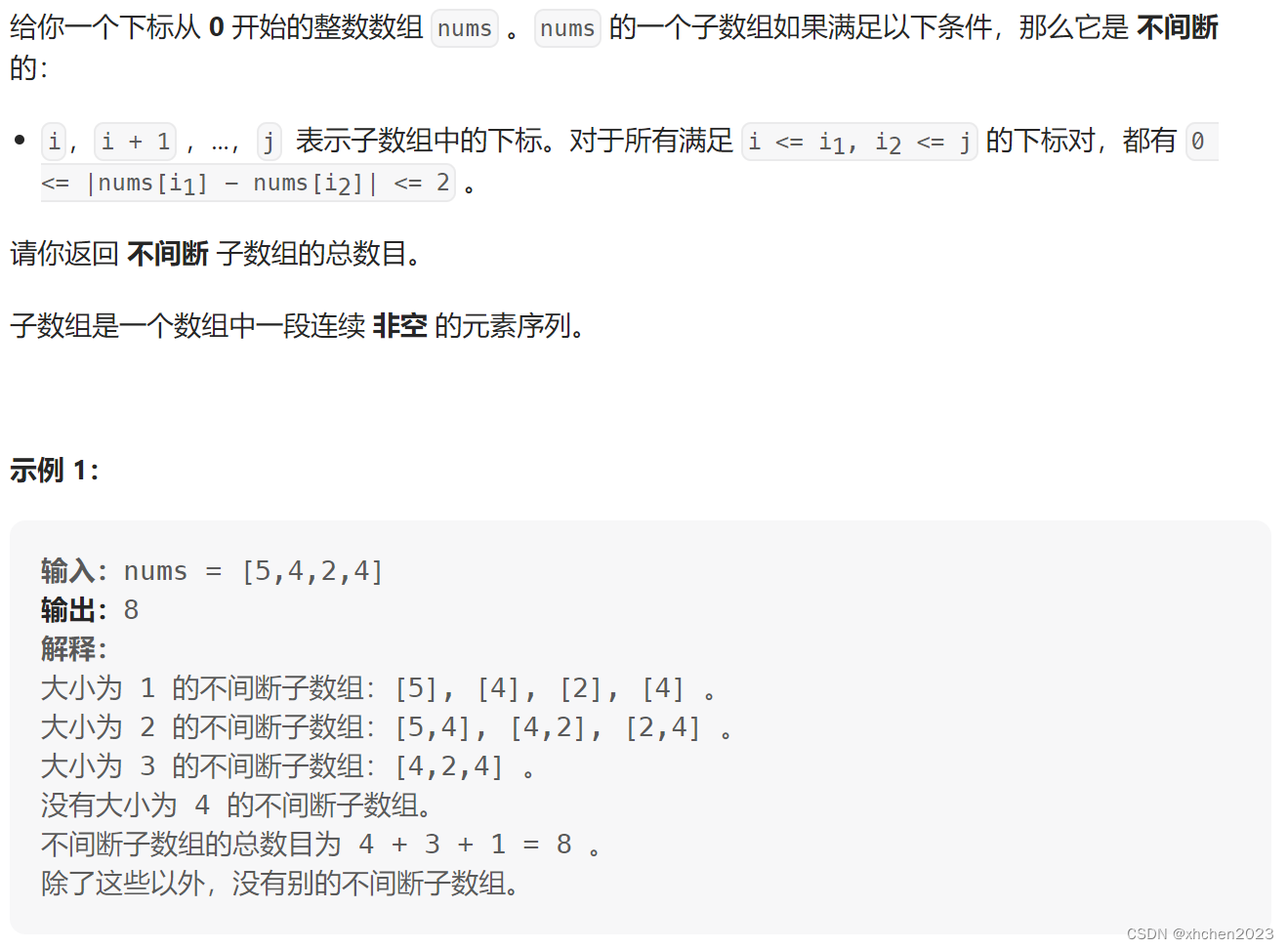
滑动窗口: 若一个数组是不间断子数组则其任意子数组都是不间断子数组, 所以可以用滑动窗口来枚举窗口的右端点$r$, 设此时窗口的左端点最小为$l$, 则以$r$为子数组右端点的不间断子数组的数目为$r-l+1$. 中途用堆维护窗口内的最大值和最小值, 同时用哈希表记录一个数值在窗口内出现的次数.

class Solution {
public:
    long long continuousSubarrays(vector<int> &a) {
        int n = a.size();
        long long res = 0;
        unordered_map<int, int> cnt;//哈希表记录窗口内数出现次数
        priority_queue<int, vector<int>, greater<int>> minheap;//最小堆
        priority_queue<int> maxheap;//最大堆
        for (int l = 0, r = 0; r < n; r++) {//枚举窗口右端点为r的情况
            minheap.push(a[r]);
            maxheap.push(a[r]);
            cnt[a[r]]++;
            while (1) {// 可能需要更新窗口左端点
                while (!cnt[maxheap.top()])//删除不在窗口内的元素
                    maxheap.pop();
                while (!cnt[minheap.top()])//删除不在窗口内的元素
                    minheap.pop();
                if (!maxheap.empty() && !minheap.empty() && maxheap.top() - minheap.top() > 2)//更新窗口左端点
                    cnt[a[l++]]--;
                else
                    break;
            }
            res += r - l + 1;
        }
        return res;
    }
};

滑动窗口+多重集: 枚举子数组的长度$len$, 对相同长度的子数组使用滑动窗口的方式从左往右遍历, 用多重集维护当前窗口内的元素, 在窗口移动过程(右端点右移和左端点右移)中维护当前的不平衡数字.

class Solution {
public:
    int sumImbalanceNumbers(vector<int> &a) {
        int n = a.size();
        int res = 0;
        multiset<int> s;//多重集中可以含相同元素
        for (int len = 2; len <= n; len++) {//枚举子数组的长度len
            s.clear();//清0
            int cur = 0;
            for (int i = 0; i < len - 1; i++)
                s.insert(a[i]);
            for (auto x = s.begin(); next(x) != s.end(); x++)//对应[0,len-1)区间
                if (*next(x) - *x > 1)
                    cur++;
            for (int l = 0, r = len - 1; r < n; l++, r++) {//枚举长为len的子数组的右端点r
                int d = 0;
                auto loc = s.upper_bound(a[r]);// a[r]需要插入至loc处
                if (loc != s.begin()) {
                    if (loc != s.end() && *loc - *prev(loc) > 1)// 多重集插入前 loc与其前驱不平衡, 所以变化量 -1
                        d--;
                    if (a[r] - *prev(loc) > 1)// 多重集插入后 a[r]与其前驱不平衡, 所以变化量 +1
                        d++;
                }
                if (loc != s.end() && *loc - a[r] > 1)// 多重集插入后 a[r]与其后驱不平衡, 所以变化量 +1
                    d++;
                s.insert(loc, a[r]);//添加a[r]
                cur += d;//更新当前的不平衡数
                res += cur;
                d = 0;
                loc = s.lower_bound(a[l]);//多重集中loc处的a[l]需要被删除
                if (loc != s.begin() && *loc - *prev(loc) > 1)// 删除前loc与其前驱不平衡, 所以变化量 -1
                    d--;
                if (next(loc) != s.end() && *next(loc) - *loc > 1)// 删除前loc与其后驱不平衡, 所以变化量 -1
                    d--;
                if (loc != s.begin() && next(loc) != s.end() && *next(loc) - *prev(loc) > 1)//loc前驱与其后驱在删除后不平衡, 所以变化量 +1
                    d++;
                cur += d;//更新当前的不平衡数
                s.erase(loc);//删除a[l]
            }
        }
        return res;
    }
};