目录
- Specular Term(高光项)
- Ambient Term(环境光照项)
- Blinn-Phong Reflection Model
- Shading Frequencies(着色频率)
- Shade each triangle(flat shading)在每个三角形上进行着色
- Shade each vertex (Gouraud shading)(顶点着色)
- Shade each pixel (Phong shading)
- Defining Per-Vertex Normal Vectors(定义每个顶点的法向量)
- Defining Per-Pixel Normal Vectors(定义每个像素的法向量)
- Graphics (Real-time Rendering) Pipeline 图形(实时渲染)管线
- Vertex Processing(顶点处理)
- Rasterization(光栅化)
- Fragment Processing(片元处理)
- Texture Mapping(纹理映射)
- 参考资源
Specular Term(高光项)
继续上节课的内容,上节课讲完了漫反射部分,这节课从高光部分开始讲。
当观察方向和镜面反射的方向接近的时候可以看到高光,其它的时候都看不到。
也就是下图中
v
⃗
\vec{v}
v和
R
⃗
\vec{R}
R足够接近的时候:
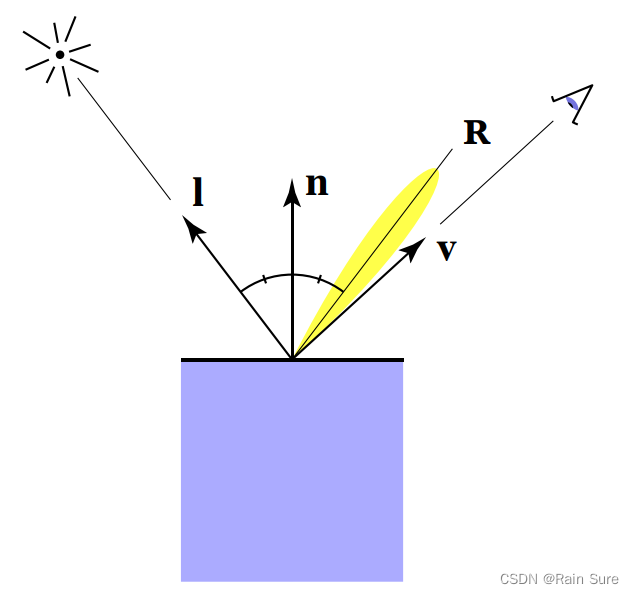
当观测方向
v
⃗
\vec{v}
v和反射方向
R
⃗
\vec{R}
R足够接近的时候,就等价于法线方向
n
⃗
\vec{n}
n和半程向量
h
⃗
\vec{h}
h足够接近。
如下图所示:
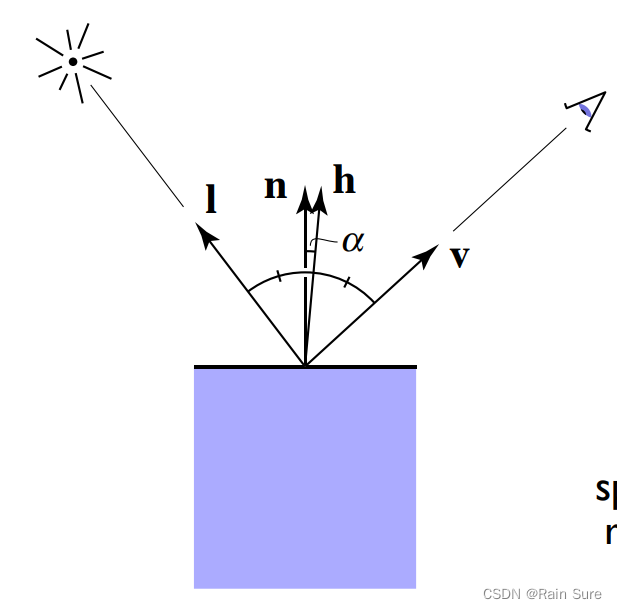
因此,高光部分的亮度就可以得到计算公式了:
其中, k s k_s ks是镜面反射系数,通常认为它是白的颜色。
之所以使用 n ⃗ \vec{n} n和 h ⃗ \vec{h} h来计算夹角,是因为半程向量 h ⃗ \vec{h} h非常好算。

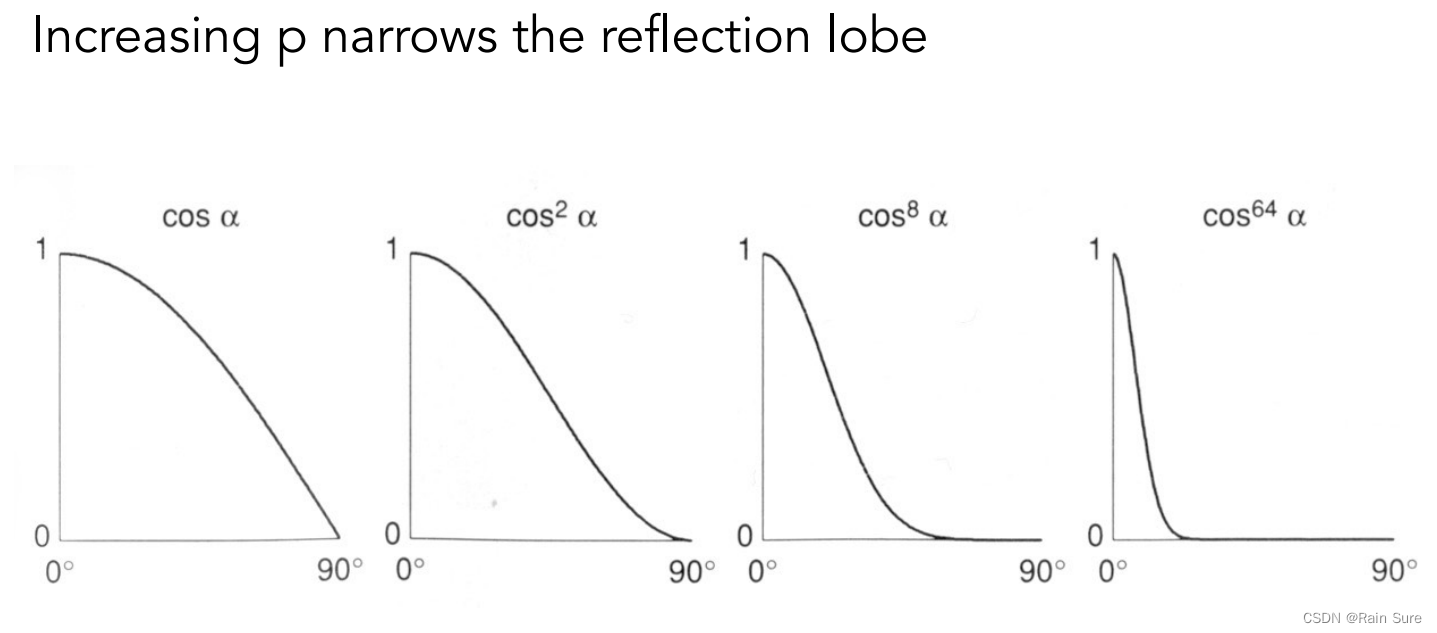
上图中的指数
p
p
p是为了降低容忍,因为高光通常是一个非常小的部分,如果不加这个指数
p
p
p会导致当夹角较大的时候仍然可以看到一个比较亮的高光,这是错误的。
在Blinn-Phong模型中, p p p通常取值为 100 100 100 ~ 200 200 200。
Ambient Term(环境光照项)
我们大胆假设环境中任何一点接收到的环境光强度都是一样的 I a I_a Ia,并且具有一个环境光系数 k a k_a ka。
环境光强度为 L a = k a I a L_a = k_a I_a La=kaIa,这是一个常数。
这是错误的,如果要求出真实的环境光,需要应用到全局光照等知识,暂且不表。
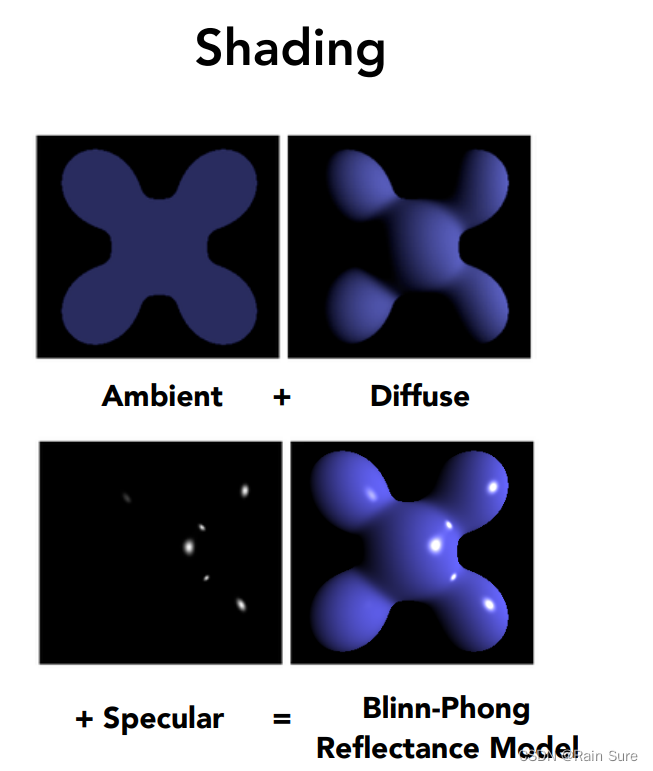
Blinn-Phong Reflection Model
现在把漫反射、环境光、高光三个部分全都加起来,就得到了Blinn-Phong反射模型:
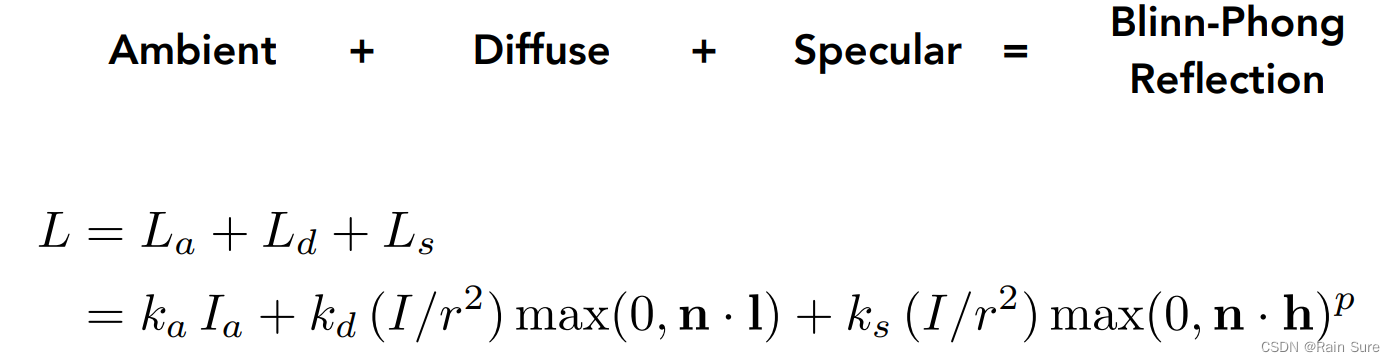
Shading Frequencies(着色频率)
着色频率是什么?
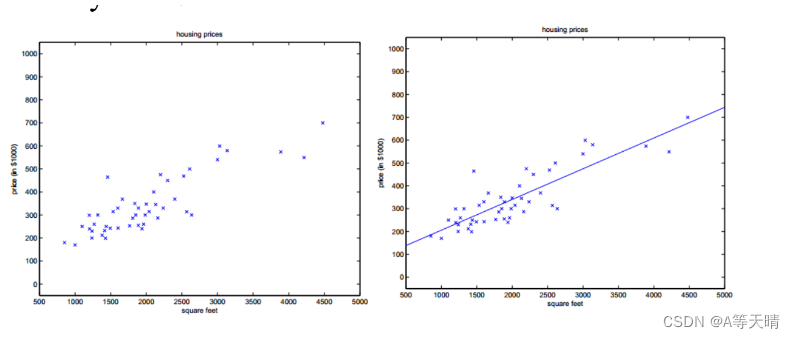
下图中的三个球完全相同,但是着色的结果各不相同。
第一个球是对每一个平面进行一次着色,计算这个平面的法线,然后计算着色。
第二个球是针对每个顶点计算一个法线,然后做一次着色,三个顶点内部三角形的颜色通过插值计算出颜色。
第三个球是针对每个像素做一次着色,针对每个三角形,利用其三个顶点的法向计算出三角形内部每个像素的法向,然后做一次着色。

Shade each triangle(flat shading)在每个三角形上进行着色
算出这个三角形平面的法线,然后进行着色,在三角形内部是完全一致的。

Shade each vertex (Gouraud shading)(顶点着色)
针对每个顶点计算一个法线,然后进行着色;在每个三角形内部,通过插值的方法计算出每个像素的着色。

Shade each pixel (Phong shading)
针对每个三角形,利用其三个顶点的法向计算出三角形内部每个像素的法向,然后做一次着色。

Defining Per-Vertex Normal Vectors(定义每个顶点的法向量)
通过许多三角形面来推断出这个点的法向量:
相邻的面的法线求平均:
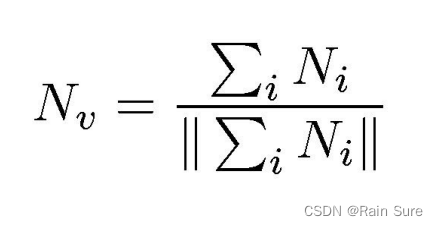
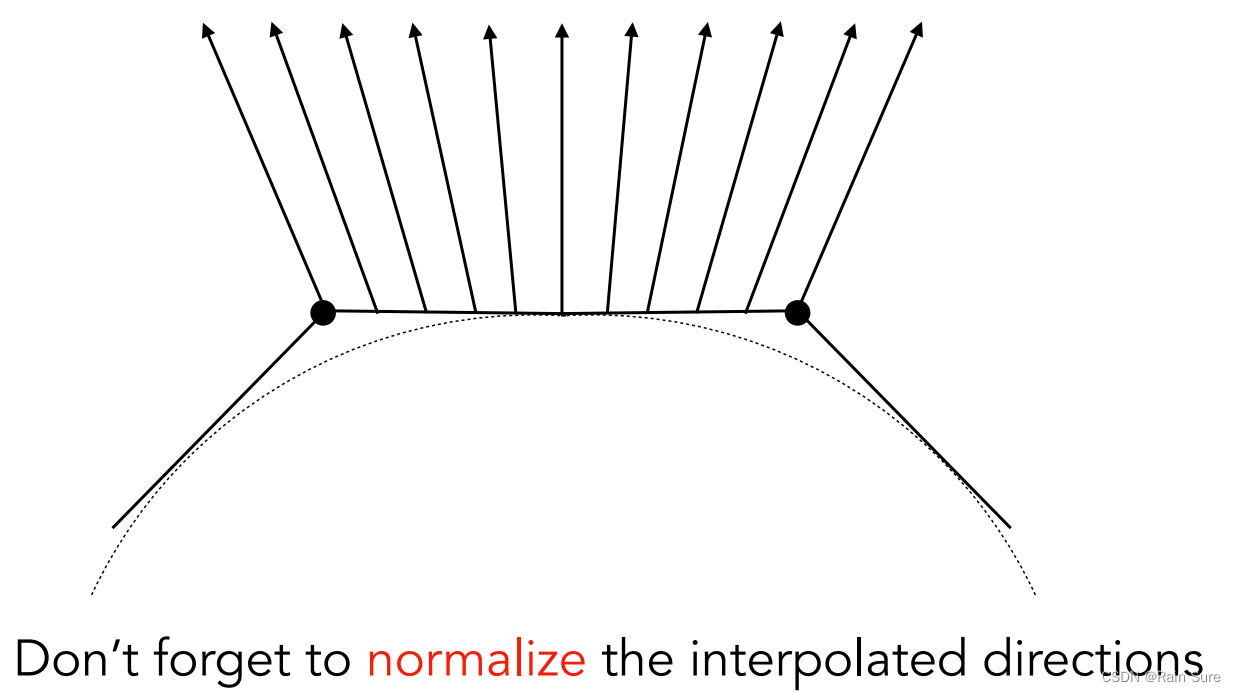
Defining Per-Pixel Normal Vectors(定义每个像素的法向量)
利用各个顶点的重心坐标插值进行计算:
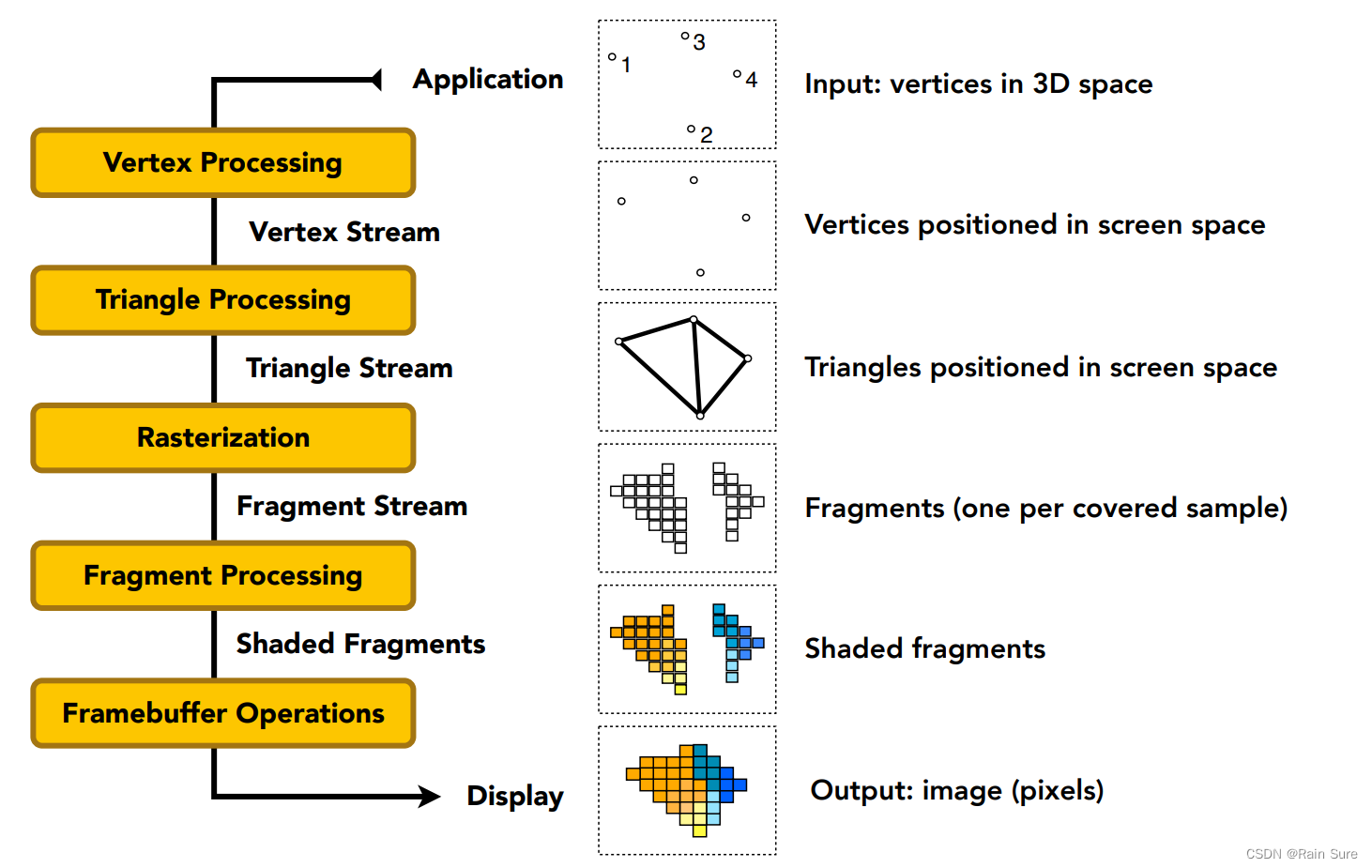
Graphics (Real-time Rendering) Pipeline 图形(实时渲染)管线
如何从场景到一张图,这中间到底经历了什么样的过程?
- 首先,输入三维空间中的许多点
- 经过一系列变换,将三维空间中的点投影到屏幕空间中。
- 将这些屏幕空间中的点按照原来的三角形关系继续连接成为三角形。
- 进行光栅化,将三角形离散成为屏幕中的fregments。
- 对每个fragments进行着色。
- 帧缓冲操作,得到每个像素的颜色,最终输出结果。(例如:如果利用了MSAA算法,需要将许多个fragments拼接成一个像素)。
Vertex Processing(顶点处理)
MVP变换,Model, View, Projection transforms
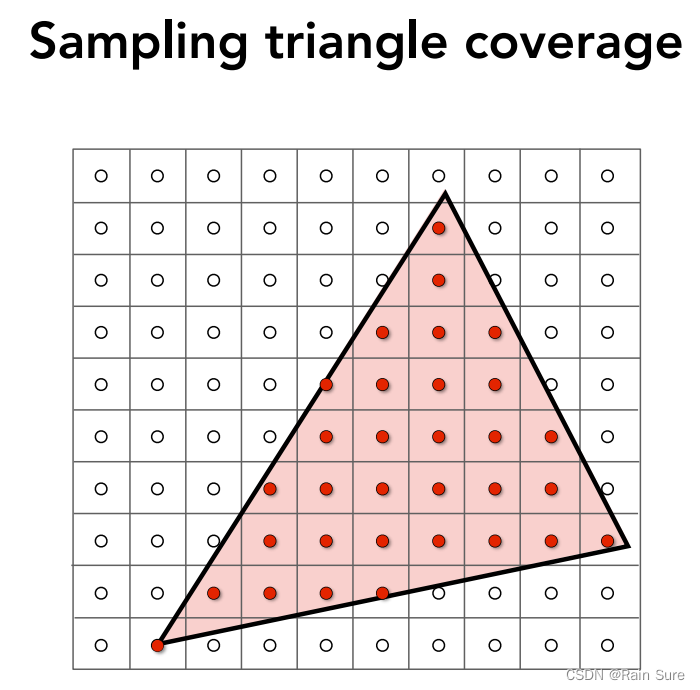
Rasterization(光栅化)
Fragment Processing(片元处理)
例如深度缓冲处理

着色处理:
纹理映射:

Texture Mapping(纹理映射)
任何一个三维物体的表面都是二维的:
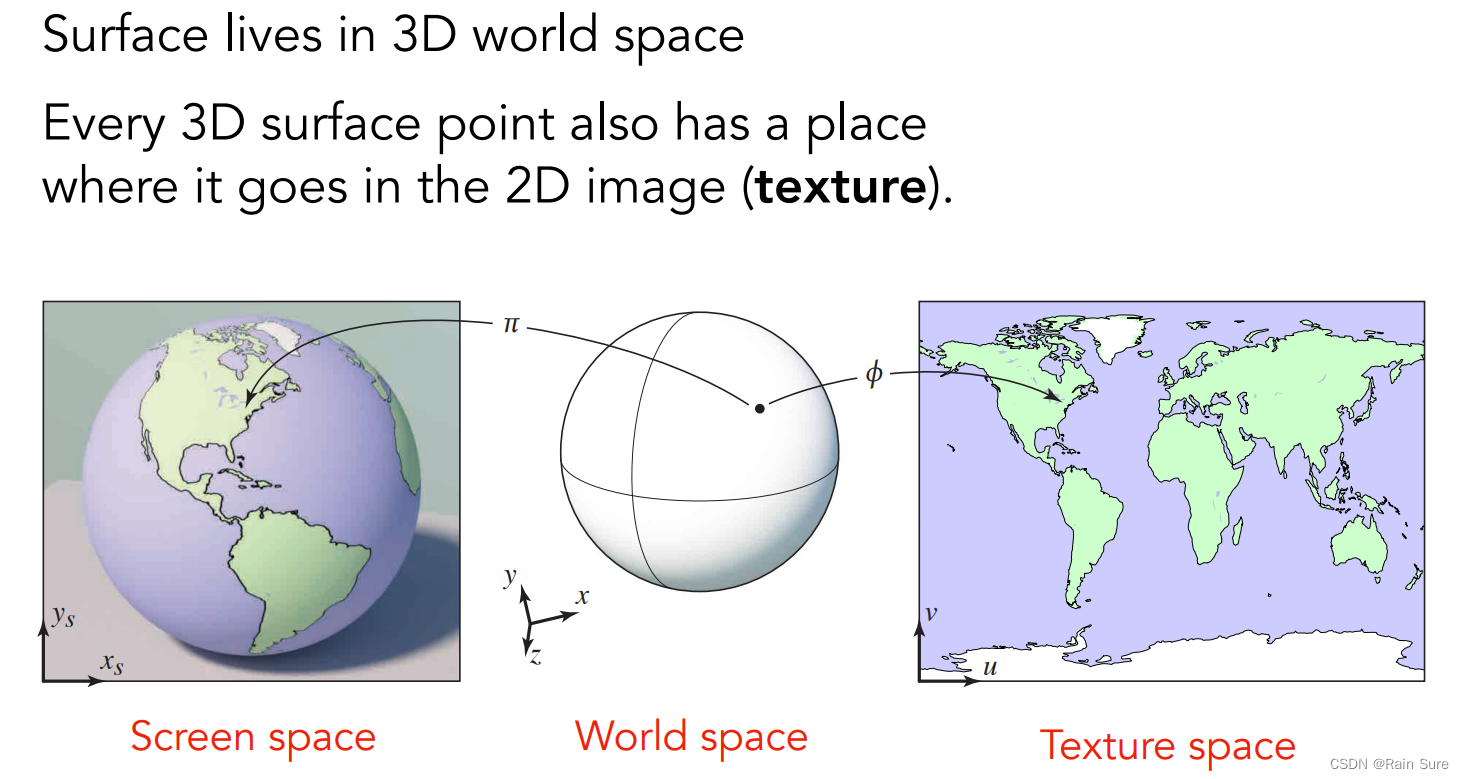
物体表面任何一个点和纹理上的点是一一对应的,这就是纹理映射。
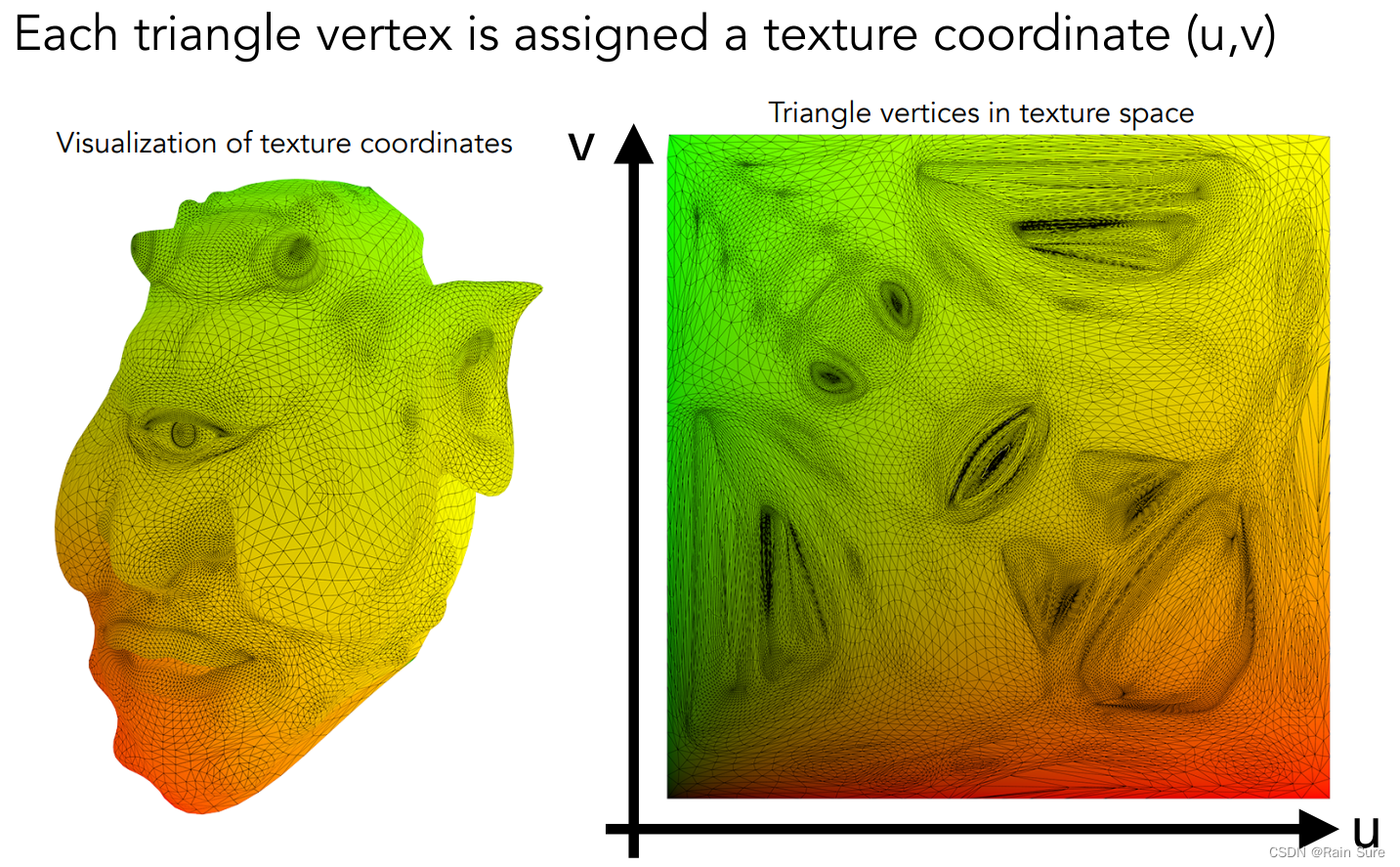
每一个三角形顶点都被指定了一个纹理坐标 ( u , v ) (u, v) (u,v)。
参考资源
GAMES101 Lecture08