北京大学2018计算机学科夏令营上机考试

news2024/9/30 15:35:54

 

目录

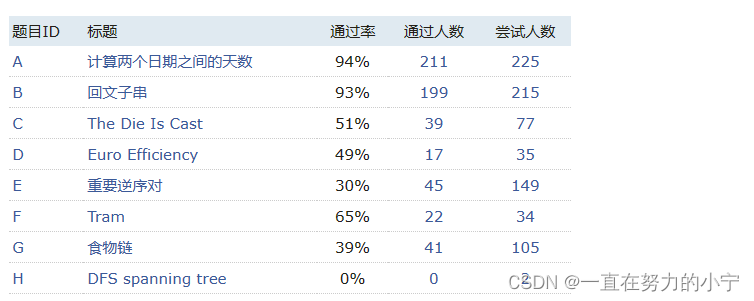
A:计算两个日期之间的天数【暴力不水】   

B:回文子串【暴力不水】

C:The Die Is Cast【DFS】

D:Euro Efficiency【看不懂】  

E:重要逆序对【归并排序】

F:Tram【看不懂】

G:食物链【图】

H:DFS spanning tree【不会】

A:计算两个日期之间的天数【暴力不水】

//http://bailian.openjudge.cn/xly2018/A/
#include<iostream>
using namespace std;
int main(){
	int a[]={0,31,28,31,30,31,30,31,31,30,31,30,31};
	int sy,sm,sd;
	int ey,em,ed;
	int sum=0,sum1=0;
	cin>>sy>>sm>>sd;
	cin>>ey>>em>>ed;
	for(int i=1;i<sy;i++){
		sum+=365;
		if(i%4==0&&i%100!=0||i%400==0)
			sum++;
	}
	for(int i=1;i<sm;i++){
		sum+=a[i];
		if(i==2&&(sy%4==0&&sy%100!=0||sy%400==0))
		sum++;
	}
	sum+=sd;
	for(int i=1;i<ey;i++){
		sum1+=365;
		if(i%4==0&&i%100!=0||i%400==0)
			sum1++;
	}
	for(int i=1;i<em;i++){
		sum1+=a[i];
		if(i==2&&(ey%4==0&&ey%100!=0||ey%400==0))
		sum1++;
	}
	sum1+=ed;
	cout<<sum1-sum<<endl;
	return 0;
}

B:回文子串【暴力不水】

这个题做了好久……我是傻逼

#include<iostream>
#include<cmath>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
char jiequ[100];
bool huiwen(string a){
	int len=a.length();
	int maxx=1;
	int flag=1;
	for(int i=0;i<len/2+1;i++){
		if(a[i]!=a[len-i-1]) flag=0;
	}
	if(flag==0) return 0;
	return 1;
}
int main(){
	int n;
	cin>>n;
	string ch;
	for(int i=0;i<n;i++){
		cin>>ch;
		int lenn=ch.length();
		int temp=lenn;
		int flag=0;
		for(int temp=lenn;temp>0;temp--){
			if(flag==1) break;
			for(int j=0;j<=lenn-temp;j++){
				string jiequ=ch.substr(j,temp);
		//		cout<<jiequ<<endl;
				if(huiwen(jiequ)) {
					cout<<jiequ<<endl;
					flag=1;
					break;
				}
			}
		}
	}
	return 0;
}

C:The Die Is Cast【DFS】

(1条消息) 【做练习】The Die Is Cast （搜索）_混沌神选韭菜的博客-CSDN博客

需要两层不同的dfs。第一个dfs搜连通的非背景点，而当它发现了一个新的骰子点上的像素时，调用第二层dfs。第二层dfs负责搜连通的骰子点像素。

看不懂了 谢谢

#include<iostream>
#include<algorithm>
using namespace std;

enum class Pixel: unsigned char {
	Background, 
	Die,
	DieDot
};

void DfsDie(int i, int j, int index);
void DfsDieDot(int i, int j, int index);

int w, h;
Pixel img[64][64];

bool visited[64][64];
bool visited_dieDot[64][64];

int cnt[500];
int nDie;

// 从一个像素点开始，遍历它所在的骰子
// index 为骰子的序号
void DfsDie(int i, int j, int index){
	if (i < 0 || j < 0 || i >= h || j >= w || visited[i][j] || img[i][j] == Pixel::Background) return;
	
	visited[i][j] = true;
	DfsDie(i - 1, j, index);
	DfsDie(i + 1, j, index);
	DfsDie(i, j - 1, index);
	DfsDie(i, j + 1, index);

	if (img[i][j] == Pixel::DieDot && !visited_dieDot[i][j]) {
		cnt[index]++;
		DfsDieDot(i, j, index);
	}

}

// 从一个像素点开始，遍历它所在的骰子的点
void DfsDieDot(int i, int j, int index) {
	if (i < 0 || j < 0 || i >= h || j >= w || visited_dieDot[i][j]
	|| img[i][j] != Pixel::DieDot) return;

	visited_dieDot[i][j] = true;

	DfsDieDot(i - 1, j, index);
	DfsDieDot(i + 1, j, index);
	DfsDieDot(i, j - 1, index);
	DfsDieDot(i, j + 1, index);
}


int main(){
	int nThrow = 0;
	while (++nThrow) {
		cin >> w >> h;
		if (w == 0 && h == 0) break;
		cin.get();
		for (int i = 0; i < h; i++) {
			for (int j = 0; j < w; j++) {
				char ch = cin.get();
				img[i][j] = ch == '*' ? Pixel::Die : (ch == 'X' ? Pixel::DieDot : Pixel::Background);
			}
			cin.get();
		}

		// init
		nDie = 0;
		for (int i = 0; i < h; i++)
			for (int j = 0; j < w; j++) 
				visited[i][j] = visited_dieDot[i][j] = 0;
		for (int i = 0; i < 500; i++) cnt[i] = 0;

		// 遍历、搜索
		for (int i = 0; i < h; i++)
			for (int j = 0; j < w; j++) {
				if (img[i][j] != Pixel::Background && ! visited[i][j]) DfsDie(i, j, nDie++);
			}

		// 排序
		sort(cnt, cnt + nDie);

		// 输出
		cout << "Throw " << nThrow << '\n';
		for (int i = 0; i < nDie; i++)
			cout << cnt[i] << (i == nDie - 1 ? '\n' : ' ');
		cout << endl;

	}

	return 0;
}

D:Euro Efficiency【看不懂】

E:重要逆序对【归并排序】

参考：归并排序方法解决重要逆序对问题


/*
#include<iostream>
using namespace std;
int a[10000000];
int sum;
int main(void){
	int N;
	cin>>N;
	for(int i=0;i<N;i++){
		cin>>a[i];
	}
	for(int i=0;i<N-1;i++){
		for(int j=i+1;j<N;j++){
			if(a[i]>2*a[j]) sum++;
		}
	}
	cout<<sum;
}
*/

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int maxn = 200010;
int array[maxn], temp[maxn];
long long ans = 0; // 存储逆序对个数，使用long long 总数能够超过int范围

void merge(int left, int mid, int right) // 归并函数
{
    int i = left; // 左边数组的起始位置
    int j = mid + 1; // 右边数组的起始位置
    int pos = left; // 递增的计数器，用于存储合并后的结果
    // 计算“重要逆序对”时不能像“逆序对”那样，将计数嵌入到归并过程当中去，会改变时间复杂度超过O(nlogn)
    while(i <= mid && j <= right) 
    {
        if(array[i] <= 2 * array[j]) // 不满足重要逆序对条件
        {
            i++; // 左边元素不需要与右边元素进行比较
        }
        else 
        {
            j++; // 右边元素满足重要逆序对条件，继续查找下一个右边元素
            ans += mid - i + 1; // 计数   i已经满足逆序条件了，所以左半部分i还没比较的肯定也满足，所以加上这些个玩意 
        }
    }
    i = left, j = mid + 1, pos = left; // 恢复初始
    while(i <= mid && j <= right) // 从小到大排序存储
    {
        if(array[i] <= array[j]) // 左边元素小于等于右边元素
        {
            temp[pos++] = array[i++]; // 存储左边元素
        }
        else 
        {
            temp[pos++] = array[j++]; // 存储右边元素
            // ans += mid-i+1; // 在“逆序对”中，直接在这里计数就好
        }
    }
    while(i <= mid) // 将剩下的左边元素存储到temp数组中
    {
        temp[pos++] = array[i++];
    }
    while(j <= right) // 将剩下的右边元素存储到temp数组中
    {
        temp[pos++] = array[j++];
    }
    for(int i = left; i <= right; i++) // 将temp数组中的结果复制回array数组
    {
        array[i] = temp[i];
    }
}

void mergesort(int left, int right) // 归并排序函数
{
    if(left < right) // 当left小于right时，继续分割数组
    {
        int mid = (left + right) / 2; // 分割数组的中间位置
        mergesort(left, mid); // 对左边数组继续递归排序
        mergesort(mid + 1, right); // 对右边数组继续递归排序
        merge(left, mid, right); // 合并左右数组
    }
}

int main()
{
    // freopen("input.txt", "r", stdin); // 打开输入文件
    int n;
    scanf("%d", &n); // 输入数组大小
    for(int i = 0; i < n; i++)
    {
        scanf("%d", &array[i]); // 输入数组元素
    }
    mergesort(0, n - 1); // 归并排序
    printf("%lld", ans); // 输出逆序对个数
    // fclose(stdin); // 关闭输入文件

    return 0;
}

上面注释掉的暴力行不通哦，时间复杂度太太太高了

F:Tram【看不懂】

G:食物链【图】

H:DFS spanning tree【不会】

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/711185.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

《微服务架构设计模式》第四章 使用Saga管理事务

《微服务架构设计模式》第四章 使用Saga管理事务

内容总结自《微服务架构设计模式》 使用Saga管理事务 一、XA解决方案存在问题二、使用Saga管理事务Saga是什么补偿事务是什么Saga协调模式协同式Saga编排式Saga 隔离性Saga结构 三、总结 一、XA解决方案存在问题 在多个服务、数据库和消息代理之间维持数据一致性的传统方式是采…
阅读更多...
小黑重庆归来，眼睛复查顺利，见到了三年没见的线上同门的leetcode之旅:剑指 Offer II 015. 字符串中的所有变位词

小黑重庆归来，眼睛复查顺利，见到了三年没见的线上同门的leetcode之旅:剑指 Offer II 015. 字符串中的所有变位词

小黑代码1:滑动窗口 class Solution:def findAnagrams(self, s: str, p: str) -> List[int]:# 字符串长度n_s len(s)n_p len(p)if n_s < n_p:return []# 差值数组arr [0] * 26# 初始窗口for i in range(n_p):arr[ord(p[i])-97] - 1arr[ord(s[i])-97] 1# 计算初始窗口…
阅读更多...
Web服务器群集：Tomcat配置https证书

Web服务器群集：Tomcat配置https证书

目录 一、理论 1.SSL 2.HTTPS协议和HTTP协议的区别 3.https证书配置 4.tomcat强制使用https 二、实验 1.https证书配置过程 2.tomcat强制使用https 三、总结 一、理论 1.SSL &#xff08;1&#xff09;概念 SSL是网络加密传输协议&#xff0c;是支持在网络服务器(主…
阅读更多...
chatgpt赋能python：烧录代码过程是怎样的

chatgpt赋能python：烧录代码过程是怎样的

烧录代码过程是怎样的 烧录代码是将编写好的程序代码烧录进内置闪存器件&#xff08;Flash&#xff09;或外部存储器&#xff08;SD卡、EEPROM等&#xff09;中的过程。本文将介绍烧录代码的具体过程和常用工具&#xff0c;以及一些注意事项。 烧录代码的步骤 步骤一&#x…
阅读更多...
分布式负载均衡 Ribbon

分布式负载均衡 Ribbon

一、Ribbon简介 是Netfix发布的负载均衡&#xff0c;Eureka一般配合Ribbon进行使用&#xff0c;基于HTTP和TCP的客户端负载均衡工具。 只有负载均衡的能力&#xff0c;不具有发送请求的能力&#xff0c;要配合服务通信组件。 RestTemplate 针对各种类型的 HTTP 请求都提供了相…
阅读更多...
青少年机器人技术一级考试备考重点（一）：机器人常识

青少年机器人技术一级考试备考重点（一）：机器人常识

随着机器人技术的飞速发展&#xff0c;越来越多的青少年开始关注并参与其中。青少年机器人技术考试作为一项评估学生机器人技术水平的重要考试&#xff0c;备受广大青少年和家长的关注。为了更好地备战青少年机器人技术一级考试&#xff0c;了解考试的学习要点和备考重点是非常…
阅读更多...
LeetCode-67. 二进制求和

LeetCode-67. 二进制求和

LeetCode-67. 二进制求和 1、题目描述2、解题思路3、代码实现4、解题记录 ) 1、题目描述 题目描述&#xff1a; 给你两个二进制字符串 a 和 b &#xff0c;以二进制字符串的形式返回它们的和。 示例1&#xff1a; 输入:a “11”, b “1” 输出&#xff1a;“100” 示例2&…
阅读更多...
kafka实现消息接受和发送

kafka实现消息接受和发送

1、首先引入依赖 <dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId> </dependency> <dependency><groupId>org.springframework.kafka</groupId><artifactId>spr…
阅读更多...
第九十五天学习记录：C++核心：类和对象Ⅳ（五星重要）

第九十五天学习记录：C++核心：类和对象Ⅳ（五星重要）

C对象模型和this指针 成员变量和成员函数分开存储 在C中&#xff0c;类内的成员变量和成员函数分开存储只有非静态成员变量才属于类的对象上 #include<iostream> using namespace std;class Person {int m_A;//非静态成员变量 属于类的对象上static int m_B;//静态成…
阅读更多...
Gradio库的Gallery模块介绍与select方法详解

Gradio库的Gallery模块介绍与select方法详解

❤️觉得内容不错的话&#xff0c;欢迎点赞收藏加关注&#x1f60a;&#x1f60a;&#x1f60a;&#xff0c;后续会继续输入更多优质内容❤️ &#x1f449;有问题欢迎大家加关注私戳或者评论&#xff08;包括但不限于NLP算法相关&#xff0c;linux学习相关&#xff0c;读研读博…
阅读更多...
Flask boostrap实现图片视频上传下载展示

Flask boostrap实现图片视频上传下载展示

Flask boostrap实现图片视频上传下载展示 1、展示效果2、前端代码3、后端代码 1、展示效果 项目目录结构 2、前端代码 html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title>&l…
阅读更多...
Go 程序是怎样跑起来的

Go 程序是怎样跑起来的

Go 程序是怎样跑起来的 引入 我们从一个 helloworld 的例子开始 package mainimport "fmt"func main() {fmt.Println("hello world") }用 vim 要打开&#xff0c;输入命令&#xff1a; :%!xxd下面是输出 00000000:7061 636b 6167 6520 6d61 696e 0a0a…
阅读更多...
tomcat概述，优化，多实例部署

tomcat概述，优化，多实例部署

目录 一、概述 二、三个容器 1、Web 容器&#xff1a; 2、Servlet 容器&#xff1a; 3、JSP 容器&#xff1a; 三、Tomcat 功能组件结构 四、优化 1、启动速度优化 2、配置参数优化 五、多实例部署 一、概述 Tomcat 是 Java 语言开发的&#xff0c;Tomcat 服务器是一…
阅读更多...
ubuntu下安装docker遇到的问题

ubuntu下安装docker遇到的问题

如果你还没有安装虚拟机&#xff0c;推荐一篇关于安装Ubuntu的详细教程&#xff1a; VMware虚拟机安装Ubuntu20.04详细图文教程https://blog.csdn.net/weixin_41805734/article/details/120698714首先&#xff0c;安装docker的前提是虚拟机能够联网&#xff0c;如果能看到右上…
阅读更多...
官方文档中docker安装php插件xdebug

官方文档中docker安装php插件xdebug

docker安装php插件 直接上代码常见问题如果查看系统类型如何查看xdebug合适的版本安装异常提示Cannot find autoconf. Please check your autoconf installation and the$PHP_AUTOCONF environment variable. Then, rerun this script.configure: error: in /tmp/pear/temp/pea…
阅读更多...
Zookeeper 分布式锁

Zookeeper 分布式锁

优质博文&#xff1a;IT-BLOG-CN 一、简介 随着公司业务的发展&#xff0c;单机应用已经无法支撑现有的用户量&#xff0c;之前采用synchronized和Lock锁已经无法满足分布式系统的要求。我们应用程序目前都会运行120台&#xff0c;节假日会扩容至240台&#xff0c;属于多JVM环…
阅读更多...
领域事件驱动（二）聚合与聚合根的了解

领域事件驱动（二）聚合与聚合根的了解

上一章对值对象以及实体进行了一些简单的讲解&#xff1a; 聚合 聚合&#xff1a;我们把一些关联性极强、生命周期一致的实体、值对象放到一个聚合里。 聚合有一个聚合根和上下文边界&#xff0c;这个边界根据业务单一职责和高内聚原则&#xff0c;定义了聚合内部应该包含哪…
阅读更多...
U-Boot移植 - 2_环境搭建和u-boot烧录启动

U-Boot移植 - 2_环境搭建和u-boot烧录启动

文章目录 1. 编译环境搭建1.1 交叉编译器下载1.2 交叉编译器安装 2. 编译原厂uboot3. 烧录开发板3.1 烧录到SD卡3.2 启动开发板 1. 编译环境搭建 1.1 交叉编译器下载 嵌入式Linux开发&#xff0c;程序编译通常在电脑端的Linux&#xff08;如虚拟机中的Ubuntu)下进行编译&…
阅读更多...
阿里云ECS部署

阿里云ECS部署

nginx 安装nginx # 查看dnf版本 dnf --version# 查找是否是否安装 dnf search nginx# 安装nginx dnf install nginx# 启动nginx systemctl start nginx# 查看nginx运行状态 systemctl status nginx# 相当于开机自启&#xff08;重启服务器&#xff0c;nginx自动启动&#xff…
阅读更多...
GoLand下载、安装

GoLand下载、安装

一、Goland下载 官方最新版本下载地址&#xff1a; Download GoLand: A Go IDE with extended support for JavaScript, TypeScript, and databases 其他版本下载&#xff1a; Other Versions - GoLand 二、安装过程 1.下载好goland-2021.1.1安装包后&#xff0c;双击运行安装包…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023