前言:
- 大家好,我是良辰丫,第十九篇,牛客网选择题+编程题汽水瓶+ 查找两个字符串a,b中的最长公共子串(动态规划问题).💞💞💞
- 生活就像一只盲盒,藏着意想不到的辛苦,当然也有万般惊喜的可能。不管是次次都如愿以偿,还是赢面寥寥无几,终究起起伏伏才是常态。我们既有过顺遂,也难免绝望,但若一陷入困境就立即抽身而退,那就再也没有翻盘的可能。只要生活还在继续,就有赢的可能。
🧑个人主页:良辰针不戳
📖所属专栏:百日冲大厂
🍎励志语句:生活也许会让我们遍体鳞伤,但最终这些伤口会成为我们一辈子的财富。
💦期待大家三连,关注,点赞,收藏。
💌作者能力有限,可能也会出错,欢迎大家指正。
💞愿与君为伴,共探Java汪洋大海。

目录
- 1. 选择题
- 2. 编程题
- 2.1 汽水瓶
- 2.2 查找两个字符串a,b中的最长公共子串
1. 选择题

- 线性表包含链表和顺序表(数组).
- 顺序表既要逻辑地址连续,存取顺序也要连续(物理地址连续).
- 链表要求逻辑地址连续,物理地址不连续.

- 栈遵循先进后出原则.
- 依次入栈,所以出栈序列为入栈序列反过来.

- 非完全二叉树不能采用顺序表的存储结构,因为非完全二叉树会有空节点,不便于统计位置关系.
- 二叉树中只有完全二叉树可以使用数组存储.

- 递归函数是自己调用自己的函数.
- 递归最终结束是因为有一个不调用自己的结束条件.

- 二叉树遍历中前序+中序或者中序加后序可以推断出另外一种遍历方式,由此我们要记住推断遍历方式一定有中序.
- 后序遍历(前序遍历)可以找到根节点,中序遍历可以给二叉树分支.

- 我们从左往右先还原二叉树.
- 然后根据前序遍历根左右还原前序遍历的序列.

- 堆分为大根堆和小根堆.
- 大根堆的堆比孩子节点大.
- 小根堆的堆比孩子节点小.

用一系列的关键字除以13取余数,结果为1的符合标准.

- 当内存中放不下所有要排序的数据,要借助外部空间(通常借助磁盘)进行排序.
- 我们学过的外部排序只有归并排序.
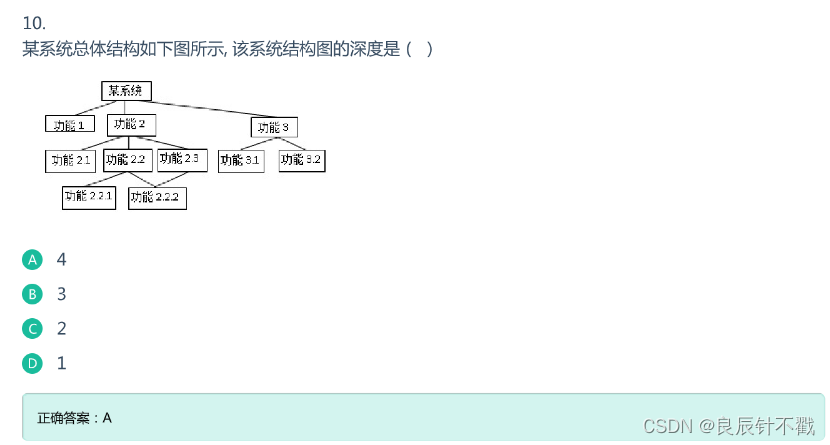
树的深度是最大节点的高度(从根节点开始算第一层).
2. 编程题
2.1 汽水瓶
做题链接:
链接: 汽水瓶
题目描述:


题目分析:
说白了这其实就是一个数学问题,理清了逻辑,问题就会迎刃而解了.
- 手里有0个瓶子或者有1个瓶子只能喝0瓶,因为只有三个瓶子才可以换汽水.
- 在这里我们需要注意的是可以喝老板借瓶子,当我们的瓶子是两个的时候,可以向老板借一个瓶子,三个空瓶子换一瓶汽水,喝完汽水把空瓶子还给老板即可.
- 处理完0个与1个的空瓶子,我们就要处理2个及其2个以上的空瓶子.
- 空瓶子大于等于3的时候就可以换汽水,此时我们喝汽水的总数sum = empty / 3.
- 当然我们还要计算我们的剩余空瓶子数量,喝完汽水的空瓶子加上我们换完汽水剩余的空瓶子.empty = empty/3 + empty%3.
- 当然最后我们还要处理一下边界问题,如果空瓶子数量为2,那么我们在喝汽水的数量sum的基础上加1.
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextInt()) { // 注意 while 处理多个 case
int n = in.nextInt();
if(n == 0){
return;
}
int num = nums(n);
System.out.println(num);
}
}
private static int nums(int n){
if(n <2){
return 0;
}
int sum = 0;
int empty = n;
while(empty>=3){
sum+= empty/3;
empty = empty%3+empty/3;
}
if(empty == 2){
sum+=1;
}
return sum;
}
}
2.2 查找两个字符串a,b中的最长公共子串
做题链接:
链接: 查找两个字符串a,b中的最长公共子串
题目描述:


题目分析:
今天有见到了一个动态规划的题目,接下来跟着良辰的步伐去分析一下.
- 动态规划(dp)用到的是分治思想,也就是把一个较大的问题化解成小问题,根据小问题的解推导大问题的解(公式).
- 要想解决动态规划的问题,我们首先要去了解状态,状态转移方程,状态初始化,返回值.
- 状态也就是问题的描述,问题求的是两个字符串的最大公共子串.我们可以先归纳子问题,也就是字符串A的子串与字符串B的子串的最大公共子串,然后我们用数组下标进行描述,A的前 i 个字符与B的前 j 个字符的最长公共子串
- 状态转移方程是如何得到的呢?根据我们的状态进行推导,并且加上我们的状态的前后关联.如果A的前 i 个字符与 B的前 j 个字符相同的时候,f(i,j) = f(i - 1,j-1) + 1;不相同的时候f(i,j) = 0.这时候有人就有疑惑了,为什么不相同的时候f(i,j) = 0呢?注意我们这里返回的是最大子串的内容,不是返回它的最大长度,不相同的为0是为了重新定义(重新找)子串的初始位置.
- 返回值是最大公共子串的内容,因此我们需要记录最长公共子串的起始位置和结束位置.
import java.util.*;
public class Main {
public static String getMaxSubstr(String str1, String str2){
char[] arr1 = str1.toCharArray();
char[] arr2 = str2.toCharArray();
int len1 = arr1.length;
int len2 = arr2.length;
//最长子串的起始位置
int start = 0;
//最长子串的长度
int maxLen = 0;
//多增加一行一列,作为辅助状态
//状态: 以a的第i个字符结尾和以b的第j个字符结尾的最长公共子串的长度
int[][] maxSubLen = new int[len1 + 1][len2 + 1];
for(int i = 1; i <= len1; ++i)
{
for(int j = 1; j <= len2; ++j)
{
//如果第i个字符和第j个字符相等,则进行累加
if(arr1[i - 1] == arr2[j - 1])
{
maxSubLen[i][j] = maxSubLen[i - 1][j - 1] + 1;
//更新最长公共子串
if(maxLen < maxSubLen[i][j])
{
maxLen = maxSubLen[i][j];
start = i - maxLen;
}
}
}
}
return str1.substring(start, start + maxLen);
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
String str1;
String str2;
while(sc.hasNext()) {
str1 = sc.next();
str2 = sc.next();
//为什么要以短的为主体呢?我们要看清题哈.
if (str1.length() < str2.length())
System.out.println(getMaxSubstr(str1, str2));
else
System.out.println(getMaxSubstr(str2, str1));
}
}
}
- 在题目描述中我们看到这样一句话 : 查找两个字符串a,b中的最长公共子串。若有多个,输出在较短串中最先出现的那个。
- 因为没看清题多走了许多弯路哈哈.



一定要看清题,这道题是以短的为主体,要不然研究半天根本不知道自己为啥错了.