题目来源：https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/description/

 

 

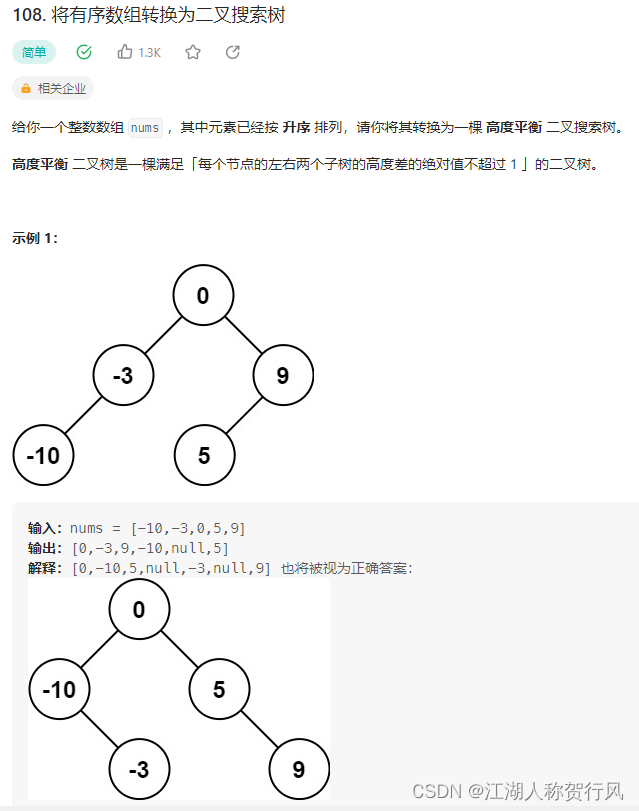
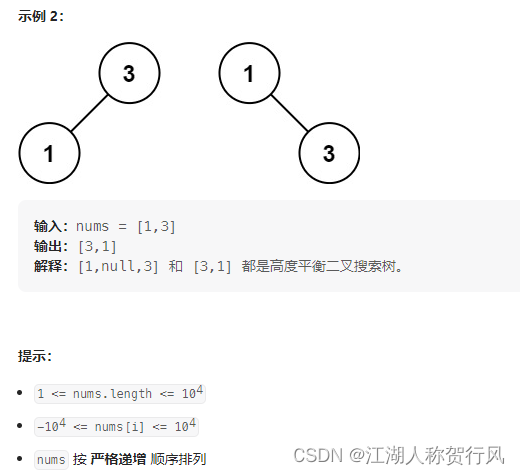
 C++题解1：递归法。由于要求是平衡树，又给出了递增数组，所以构建二叉树只需将中间值作为中间节点，左右两边分属左右子树，这样就可以不断地保证左右子树的高度平衡。重点在于区分左右区间，我采用的是左闭右闭区间，中间节点如果有两个选择左边的一个。

class Solution {
public:
    TreeNode* sorttree(vector<int>& nums, int leftind, int rightind) {
        int mid = floor((leftind + rightind) / 2);
        TreeNode* node = new TreeNode(nums[mid]);
        if(leftind == rightind) return node;
        else if(leftind > rightind) return nullptr;
        else{
            node->left = sorttree(nums, leftind, mid-1);
            node->right = sorttree(nums, mid+1, rightind);
        }
        return node;
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        int len = nums.size();
        if(len == 1) return new TreeNode(nums[0]);
        TreeNode* root = sorttree(nums, 0, len-1);
        return root;
    }
};

C++题解2：迭代法，类似层序遍历，但是用数组的值替代每一节点的值，且需要存放左右区间的索引。来源代码随想录

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        if (nums.size() == 0) return nullptr;

        TreeNode* root = new TreeNode(0);   // 初始根节点
        queue<TreeNode*> nodeQue;           // 放遍历的节点
        queue<int> leftQue;                 // 保存左区间下标
        queue<int> rightQue;                // 保存右区间下标
        nodeQue.push(root);                 // 根节点入队列
        leftQue.push(0);                    // 0为左区间下标初始位置
        rightQue.push(nums.size() - 1);     // nums.size() - 1为右区间下标初始位置

        while (!nodeQue.empty()) {
            TreeNode* curNode = nodeQue.front();
            nodeQue.pop();
            int left = leftQue.front(); leftQue.pop();
            int right = rightQue.front(); rightQue.pop();
            int mid = left + ((right - left) / 2);

            curNode->val = nums[mid];       // 将mid对应的元素给中间节点

            if (left <= mid - 1) {          // 处理左区间
                curNode->left = new TreeNode(0);
                nodeQue.push(curNode->left);
                leftQue.push(left);
                rightQue.push(mid - 1);
            }

            if (right >= mid + 1) {         // 处理右区间
                curNode->right = new TreeNode(0);
                nodeQue.push(curNode->right);
                leftQue.push(mid + 1);
                rightQue.push(right);
            }
        }
        return root;
    }
};