[数据结构 -- 手撕排序第一篇] 插入排序

news2024/9/26 5:20:53

目录

1、常见的排序算法

2、插入排序的思路

2.1 基本思想

2.2 直接插入排序

2.2.1 单趟排序的思路

2.2.2 单趟排序代码实现

3、插入排序代码

4、插入排序+打印测试

5、插入排序的时间复杂度

5.1 最坏情况

5.2 最好情况

6、直接插入排序的特性总结

1、常见的排序算法

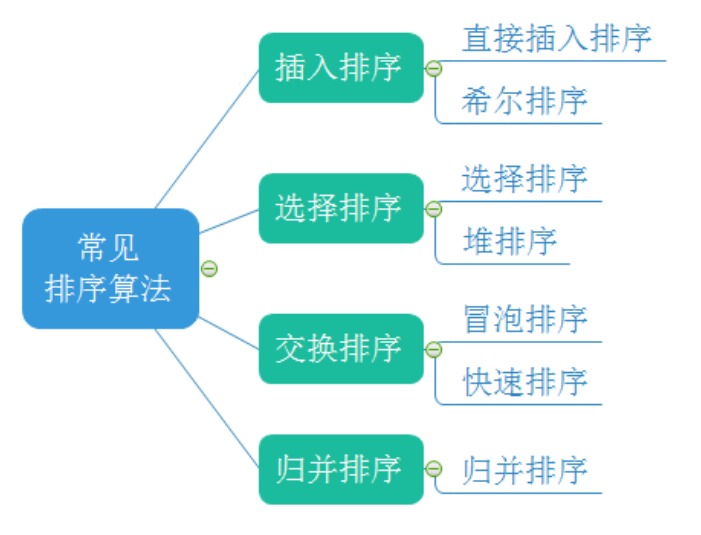
2、插入排序的思路

2.1 基本思想

直接插入排序是一种简单的插入排序法，其基本思想是：
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列。

实际中我们玩扑克牌时，就用了插入排序的思想：

2.2 直接插入排序

当插入第i(i>=1)个元素时，前面的array[0],array[1],…,array[i-1]已经排好序，此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较，找到插入位置即将array[i]插入，原来位置上的元素顺序后移。

2.2.1 单趟排序的思路

我们将数组中最后一个元素的下标记为end，每次要插进来的数字先放在end+1位置上，再用一个临时变量tmp将这个数字保存起来，从end开始依次往前比较，如果tmp比end小，就让end往后移一位，tmp再与end-1，end-2……不断比较，当tmp大于某个位置的元素时，就将tmp插入到该位置下标+1的位置上，单趟排序就完成了。

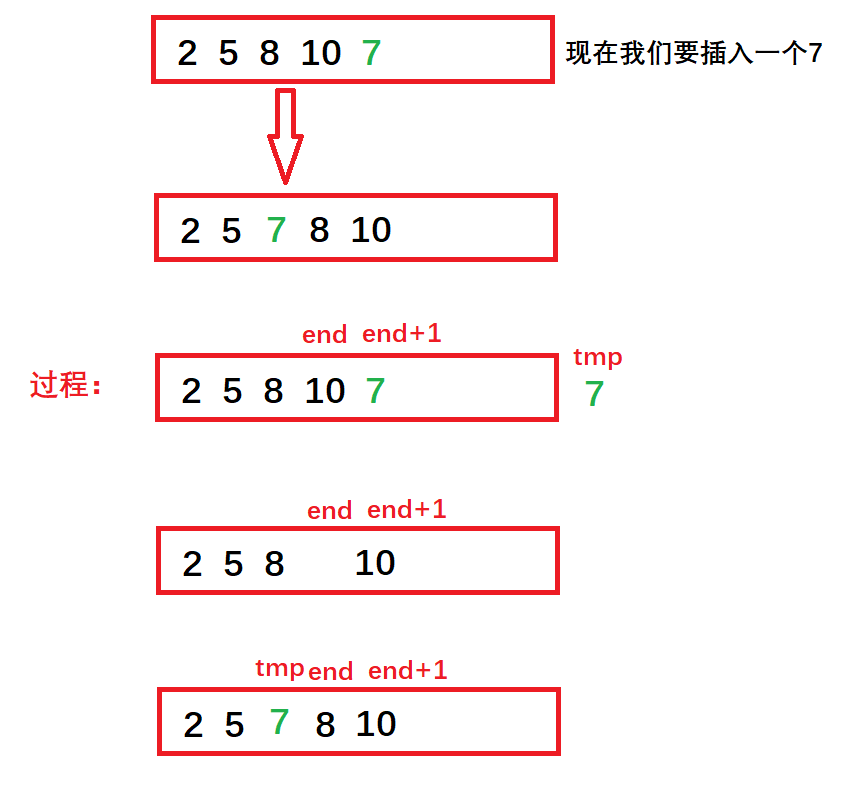
2.2.2 单趟排序代码实现

int tmp = a[end + 1];
while (end >= 0)
{
    if (a[end] > tmp)
    {
        a[end + 1] = a[end];
        end--;
    }
    else
    {
        break;
    }
}
a[end + 1] = tmp;

我们代码中有一个巧妙的写法，在 a[end] < tmp 时，跳出循环，再将tmp插入到 a[end+1] 位置。这样能同时解决 a[end] < tmp 与第一个元素<tmp 的插入。

3、插入排序代码

插入排序是在单趟排序的基础上，将整个数组排序一遍，我们给但趟排序的代码外加上一层循环，就实现了插入排序。

for (int i = 1; i < n; i++)
{
    int end = i - 1;
    int tmp = a[i];

    while (end >= 0)
    {
        if (a[end] > tmp)
        {
            a[end + 1] = a[end];
            end--;
        }
        else
        {
            break;
        }
    }
    a[end + 1] = tmp;
}

4、插入排序+打印测试

void Print(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}
void InsertSort(int* a, int n)
{
	for (int i = 1; i < n; i++)
	{
		int end = i - 1;
		int tmp = a[i];

		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tmp;
	}
}
void TestInsert()
{
	int a[] = { 9,8,7,6,5,4,3,2,1 };
	InsertSort(&a, sizeof(a) / sizeof(int));
	Print(&a, sizeof(a) / sizeof(int));
}
int main()
{
	TestInsert();
	return 0;
}

效果展示：