正态分布以及高斯函数的定义
如果随机变量
X
X
X 的密度函数为
f
μ
,
σ
(
x
)
=
1
σ
2
π
e
−
(
x
−
μ
)
2
2
σ
2
,
x
∈
R
,
σ
>
0
f_{\mu, \sigma}(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\dfrac{(x-\mu)^2}{2 \sigma^2}}, \quad x \in \mathbb{R}, \sigma>0
fμ,σ(x)=σ2π1e−2σ2(x−μ)2,x∈R,σ>0称
X
X
X 服从参数为
(
μ
,
σ
)
(\mu, \sigma)
(μ,σ) 的正态分布 (normal distribution), 也称 Gauss分布, 记为
X
∼
N
(
μ
,
σ
)
X \sim N\left(\mu, \sigma\right)
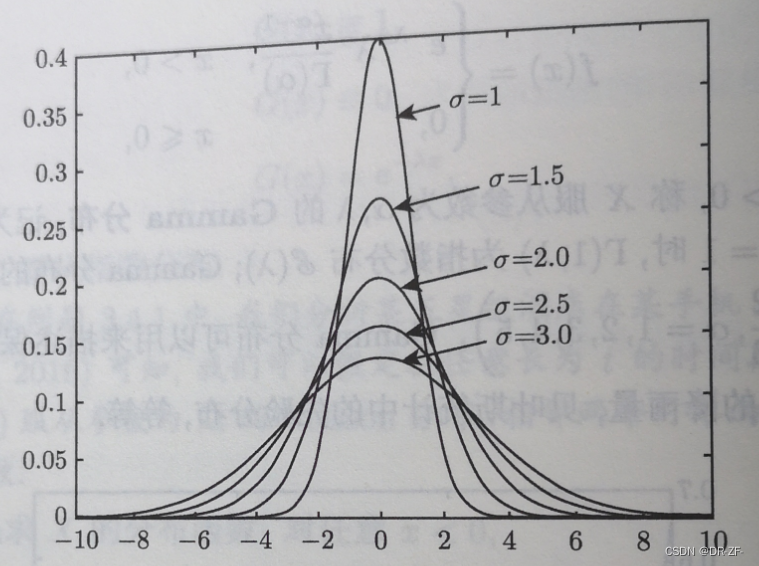
X∼N(μ,σ). 其密度函数的图像
(
μ
=
0
,
σ
=
1
,
1.5
,
2.0
,
2.5
,
3.0
)
(\mu=0, \sigma=1,1.5,2.0,2.5,3.0)
(μ=0,σ=1,1.5,2.0,2.5,3.0) 如 图 3.11 所示.
标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1)
密度函数为
ϕ
(
x
)
=
1
2
π
e
−
x
2
2
,
x
∈
R
\phi(x)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}, \quad x \in \mathbb{R}
ϕ(x)=2π1e−2x2,x∈R
分布函数为
Φ
(
x
)
=
∫
−
∞
x
ϕ
(
t
)
d
t
\Phi(x)=\int_{-\infty}^x \phi(t) \mathrm{d} t
Φ(x)=∫−∞xϕ(t)dt
正态分布的性质1
(1) 密度函数关于 μ \mu μ 对称, 在 μ \mu μ 处取最大值, 最大值为 1 2 π σ \frac{1}{\sqrt{2 \pi} \sigma} 2πσ1.
正态分布的性质2
(2) 密度函数在 x = μ ± σ x=\mu \pm \sigma x=μ±σ 处有拐点.
正态分布的性质3
(3) 若
X
∼
N
(
μ
,
σ
)
X \sim N\left(\mu, \sigma\right)
X∼N(μ,σ), 则
Y
=
X
−
μ
σ
∼
N
(
0
,
1
)
Y=\dfrac{X-\mu}{\sigma} \sim N(0,1)
Y=σX−μ∼N(0,1).
P
(
Y
⩽
y
)
=
P
(
X
−
μ
σ
⩽
y
)
=
P
(
X
⩽
μ
+
σ
y
)
=
∫
−
∞
μ
+
σ
y
f
μ
,
σ
(
x
)
d
x
=
1
2
π
σ
∫
−
∞
μ
+
σ
y
e
−
(
x
−
μ
)
2
2
σ
2
d
x
(
令
x
−
μ
σ
=
t
)
=
1
2
π
∫
∞
y
e
−
t
2
2
d
t
=
Φ
(
y
)
\begin{aligned} P(Y \leqslant y) & =P\left(\frac{X-\mu}{\sigma} \leqslant y\right) \\ & =P(X \leqslant \mu+\sigma y) \\ & =\int_{-\infty}^{\mu+\sigma y} f_{\mu, \sigma}(x) \mathrm{d} x \\ & =\frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^{\mu+\sigma y} e^{\frac{-(x-\mu)^2}{2 \sigma^2}} \mathrm{~d} x \quad\left(\text { 令 } \frac{x-\mu}{\sigma}=t\right) \\ & =\frac{1}{\sqrt{2 \pi}} \int_{\infty}^y e^{-\frac{t^2}{2}} \mathrm{~d} t \\ & =\Phi(y) \end{aligned}
P(Y⩽y)=P(σX−μ⩽y)=P(X⩽μ+σy)=∫−∞μ+σyfμ,σ(x)dx=2πσ1∫−∞μ+σye2σ2−(x−μ)2 dx( 令 σx−μ=t)=2π1∫∞ye−2t2 dt=Φ(y)
正态分布的性质4
(4)
1
2
π
∫
−
∞
+
∞
e
−
x
2
2
d
x
=
1
\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-\frac{x^2}{2}} \mathrm{~d} x=1
2π1∫−∞+∞e−2x2 dx=1.
事实上,
(
1
2
π
∫
−
∞
+
∞
e
−
x
2
2
d
x
)
2
=
(
1
2
π
∫
−
∞
+
∞
e
−
x
2
2
d
x
)
(
1
2
π
∫
−
∞
+
∞
e
−
y
2
2
d
y
)
=
1
2
π
∫
−
∞
+
∞
∫
−
∞
+
∞
e
−
z
2
+
y
2
2
d
x
d
y
=
1
2
π
∫
0
2
π
∫
0
+
∞
e
−
r
2
2
r
d
θ
d
r
=
−
e
−
r
2
2
∣
0
+
∞
=
1
\begin{aligned} \left(\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-\frac{x^2}{2}} \mathrm{~d} x\right)^2 & =\left(\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-\frac{x^2}{2}} \mathrm{~d} x\right)\left(\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-\frac{y^2}{2}} \mathrm{~d} y\right) \\ & =\frac{1}{2 \pi} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} e^{-\frac{z^2+y^2}{2}} \mathrm{~d} x \mathrm{~d} y \\ & =\frac{1}{2 \pi} \int_0^{2 \pi} \int_0^{+\infty} e^{-\frac{r^2}{2}} r \mathrm{~d} \theta \mathrm{d} r \\ & =-\left.e^{-\frac{r^2}{2}}\right|_0 ^{+\infty}=1 \end{aligned}
(2π1∫−∞+∞e−2x2 dx)2=(2π1∫−∞+∞e−2x2 dx)(2π1∫−∞+∞e−2y2 dy)=2π1∫−∞+∞∫−∞+∞e−2z2+y2 dx dy=2π1∫02π∫0+∞e−2r2r dθdr=−e−2r2
0+∞=1
正态分布的性质5
(5) Φ ( − x ) = 1 − Φ ( x ) \Phi(-x)=1-\Phi(x) Φ(−x)=1−Φ(x).
正态分布的性质6: ( 0 , σ ) (0,\sigma) (0,σ)
当 σ ⟶ 0 \sigma \longrightarrow 0 σ⟶0 时, 1 = lim σ → 0 ∫ − ∞ + ∞ 1 2 π σ e − x 2 2 σ 2 d x = ∫ − ∞ + ∞ δ ( x ) d x \begin{aligned} 1 & =\lim _{\sigma \rightarrow 0} \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{x^2}{2 \sigma^2}} \mathrm{~d} x \\ & =\int_{-\infty}^{+\infty} \delta(x) \mathrm{d} x \end{aligned} 1=σ→0lim∫−∞+∞2πσ1e−2σ2x2 dx=∫−∞+∞δ(x)dx