1. 文章简介

• 标题：Goat: Fine-tuned LLaMA Outperforms GPT-4 on Arithmetic Tasks
• 作者：Tiedong Liu, Bryan Kian Hsiang Low
• 日期：2023
• 期刊：arxiv preprint

2. 文章概括

  文章给出了一种可高精度完成基本数学运算的大模型Goat(Good at Arithmetic Tasks)，相比于GPT-4，Goat在多位数字的基本运算（加减乘除）上有大幅的精度提升。

3 文章重点技术

3.1 LLM的选择

  文章的Goat模型是在LLaMA[1]基础上进行微调的。之所以选择LLaMA，是因为研究表明分词是影响大模型数学运算能力的一个重要因素，而LLaMA对于处理数字的分词上要优于其它LLM。下表展示了文章对比的一些LLM的分词结果，可以看到LLaMA对与数字的分词是最合理最能支撑数学运算的。

3.2 算数任务的可学习性(learnability)

  算数任务可划分为两类：LLM可学习(learnable)的任务和不可学习(unlearnable)的任务。研究表明，不可学习的任务可通过链式思维(Chain-of-Thought, COT)分解为可学习的任务。
  首先，文章对基本的数学运算进行划分。为此，文章进行了数值实验，将LLM可以以较高的精度解决的任务分类为可学习任务，反之LLM表现很差的任务被分类为不可学习任务。下表为文章将数学基本运算进行的分类。其中不可学习的任务包含两种：多位数*多位数，多位数/多位数。

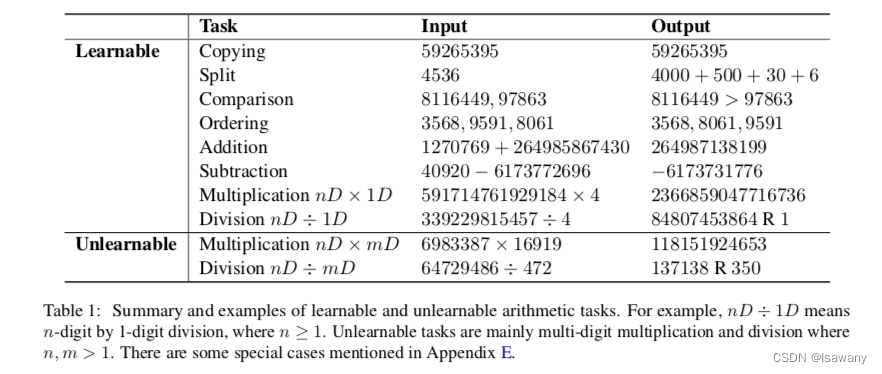
3.3 大模型的加减乘除

  按照上述分类，所有的加法和减法都是可学习的任务，模型可以成功捕获到其中的数学操作模式，得到较高精度。
  针对乘法，如上表分类，多位数*一位数是可学习的任务，但多位数*多位数是不可学习的任务。为了让LLM计算多位数*多位数，我们将其划分为5个可学习的子任务

• extraction：从自然语言指令中提取数学运算。如给定指令"Compute 126 * 234"，我们提取出其中的"126 * 234 ="这种标准的运算格式（对应上表中可学习任务-Copying）.
• split: 将二者中较小的数划分。如上述标准运算格式，我们首先找到比较小的数"126"（对应上表中可学习任务-Comparison），然后我们将"126"进行分解得到"126=100+20+6"（对应上表中可学习任务-Split）.
• expansion：按照分配律将乘法展开。如上述标准运算分解之后，我们得到"(100+20+6) * 234 = 100 * 234 + 20 * 234 + 6 * 234"（对应上表中可学习任务-Copying）.
• product：计算分配之后的每一项的乘积。如上式可演变为" 100 * 234 + 20 * 234 + 6 * 234 = 1 * 234 (end+00) + 2 *234(end+0) + 6 * 234 =23400 + 4680 + 1404"，即通过多位数*一位数和末尾补0的操作完成（对应上表中可学习任务-Multiplication+Copying）.
• adding：计算各子项之和。如上式结果求和为"23400 + 4680 + 1404 = 28080 + 1404 = 29484"即为最后结果（对应上表中可学习任务-Adding+Copying）.
    针对除法，多位数除以一位数的任务是可学习任务，现在我们考虑多位数除以多位数的任务。为此，我们通过慢除法来进行循环计算：$$R_j-D\times (q_{n-(j+1)}\times 10^j)=R_{j+1}$$，其中$n$表示被除数的位数，$R_j$表示上一轮的商，$q_{n-(j+1)}$表示模型需要计算的值，要满足$D\times q_{n-(j+1)}\times 10^j\le R_j$，$D$表示除数。上式迭代的终止条件为$R_{j+1}<D$。考虑8914/64，首先第一轮的$R_j=8914,D=64$，我们找到最大的可以使得$64\times q_{n-(j+1)}\times 10^j\le 8914$的$j$，得到$j=2$，对应的最大的$q=1$，即得到$$8914-64\times (1\times 10^2)=2514$$；接下来$R_j=2514\ge D$，则唏嘘找到最大的可以使得$64\times q_{n-(j+1)}\times 10^j\le 2514$的$j$，得到$j=1$，对应最大的$q=3$，即得到$$2514-64\times (3\times 10^1)=594$$；接下来$R_j=594\ge D$，则继续找到最大的可以使得$64\times q_{n-(j+1)}\times 10^j\le 594$的$j$，得到$j=0$，对应最大的$q=9$，即得到$$594-64\times (9\times 10^0)=18$$；最后$R_j<D=64$，终止判断。最后得到的商由上面所有的$q_{n-(j+1)}\times 10^j$组成，即$1\ast 10^2+3\ast 10^1+9\ast 10^0=139$（相当于split的反向操作），余数为剩下的$R_j=18$。注意到上述整个过程只采用了基本的可学习任务，包括Copyting, Subtraction, Comparison, Multiplication(nD*1D), 反向split。

4. 数值实验结果

  文章随机生成了一百万个问答对，其中问题的自然语言部分是由多个不同的prompt形式组成，问题中包含的数字是不超过16位的随机数字，然后按照上述标准的COT产生回答作为标注数据。模型在LLaMA基础上通过上述数据进行微调，得到Goat模型。
  下表为文章的数值实验结果，可以看到Goat-7B在所有数学任务上表现基本上都在90%甚至95%以上，在unlearnable任务上精度远超过GPT-4。

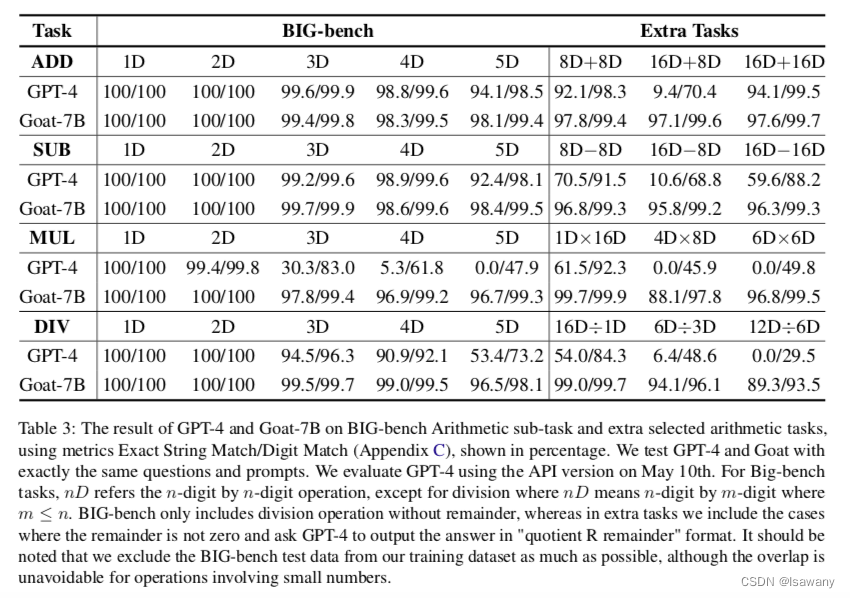
  值得一提的是，文章通过增加"Solve it step by step"在GPT-4的prompt中，引导GPT-4产生中间结果。文章发现在一些测试样例中，GPT-4产生了一些错误的中间过程，但最终答案确是正确的。这说明GPT-4可能并没有很好的利用到中间过程。
  此外，文章测试了将上述COT作为In-Context Learning的样本加入GPT-4的prompt，显著提高了GPT-4的运算能力，说明文章提出的COT是非常有效的。下图为GPT-4的一个3-shot样例。

5. 文章亮点

  文章提出了一种Chain-of-Thought(COT)方法，可以有效地解决LLM无法正确进行数学基本运算的问题。文章基于该COT训练了大语言模型Goat，在基本数学运算能力上达到了SOTA水平。

6. 原文传送门

Goat: Fine-tuned LLaMA Outperforms GPT-4 on Arithmetic Tasks

7. References

[1] 论文笔记–LLaMA: Open and Efficient Foundation Language Models