👑作者主页：@进击的安度因
🏠学习社区：进击的安度因（个人社区）
📖专栏链接：有营养的算法笔记

文章目录

一、思路
二、模板讲解
三、模板测试
四、加练 —— 逆序对的数量

今天讲解的内容是归并排序模板及其练习题 ~

一、思路

归并排序，从它的名字我们可以大约猜测这个排序的步骤。归 —— 归置，意思是整理收拾，归置原位；并 —— 合并，将序列合并回去，而归并排序的主题思路也差不多就是这样。

归并排序的思想是分治，就是递归。归并和上篇笔记的快排算是分治中的两个难点，我们学习初级算法，归并部分基本只需要吃透这两部分就 ok 。

接下来我们梳理一下 归并排序 的主要步骤：

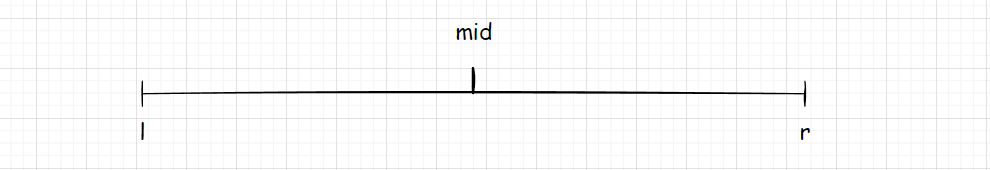
确定分界点，分界点一般为中点：mid = q[l + r >> 1]
递归排序左右区间，使区间有序
双指针合并区间

二、模板讲解

前面我们讲了主要步骤，我们再挖一下每一步该干什么，再给出模板：

第一点确定分界点没什么好说的，就是确定 每次归并排序划分区间的分界点 。

第二点的话，就是递归左右区间的问题，而递归排序之前就只是 确定分界点 而已，说明是会先 递归到最底层，然后逐渐排序，归并返回的 。

第三点的话，这一步就得好好说说：

双指针合并区间，说着容易，但是其实不是那么好实现的。

如果不借助额外空间，那么合并时，就可能会造成数据覆盖等错误情况。

所以需要借助辅助数组 tmp，排序过程中，将区间内元素有序放置于 tmp 中，当 tmp 数组对于每次归并的区间有序后，将数据倒回原数组 。

梳理一遍后，我们再看模板：

void merge_sort(int q[], int l, int r)
{
    if (l >= r)
        return; 
    // 1. 确定分界点
    int mid = l + r >> 1;   
    // 2. 递归排序左右区间
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);
    // 3. 双指针合并区间
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r)
    {
        // 写法具有稳定性
        if (q[i] <= q[j])
            tmp[k++] = q[i++];
        else
            tmp[k++] = q[j++];
    }
    // 将没合并的数据直接倒入 tmp 中
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    // 将数据倒回原数组
    for (int i = l, j = 0; i <= r; i++, j++)
    {
        q[i] = tmp[j];
    }
}

时间复杂度：O(N * logN) 空间复杂度：O(N)

接下来，对模板中的不容易理解的部分讲解一下：

1：双指针合并区间

while (i <= mid && j <= r)
{
    // 写法具有稳定性
    if (q[i] <= q[j])
        tmp[k++] = q[i++];
    else
        tmp[k++] = q[j++];
}

这一部分就是 i 和 j 对应的两区间的内容进行比较，让其有序存入辅助数组 tmp 中：

q：1    4    6    1    3    5
   i        mid   j     
 第一个 1        第二个1
tmp：1    1    3    4    5    6
 第一个1 第二个1

在这一过程中，对于相同值的数据位置保持不变，归并排序是具有 稳定性 的。

2：将没合并的内容倒入 tmp 中

while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];

假如一段区间的内容已经完全存入 tmp 中，另一段区间未存储完毕：

q：1    4    6    1    3
   i        mid   j     
tmp：1    1    3    		此时 右区间已经放置完毕，左区间还剩下 4 6
   第一个1   第二个1
   
左区间剩余元素的最小值为 4，必定大于等于 tmp 数组的最后一个元素，直接将数据倒入 tmp 中
while (i <= mid) tmp[k++] = q[i++];
tmp：1    1    3    4    6

3：将数据倒回原数组

for (int i = l, j = 0; i <= r; i++, j++)
{
    q[i] = tmp[j];
}

这里 i = l 而不是 i = 0 的原因是，我们每次归并的可能不是 一整个原数组 ，可能是一段区间，区间从 l 开始，到 r 结束。

如果看完板子还是比较模糊的话，可以下去举个例子画一下归并排序的过程，观察递归到最底层，然后逐渐归并返回。这一过程了解了，这个板子几乎也就吃透了~

三、模板测试

给定你一个长度为 n 的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式：

输入共两行，第一行包含整数 n 。

第二行包含 n 个整数（所有整数均在 1∼10^9 范围内），表示整个数列。

输出格式：

输出共一行，包含 n个整数，表示排好序的数列。

数据范围：

1 ≤ n ≤ 100000

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

AC，没问题

四、加练 —— 逆序对的数量

描述：

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对；否则不是。

输入格式：

第一行包含整数 n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式：

输出一个整数，表示逆序对的个数。

数据范围：

1 ≤ n ≤ 100000
数列中的元素的取值范围 [1, 10^9]。

输入样例：

6
2 3 4 5 6 1

输出样例：

思路：

这道题的主要思路还是 归并排序 。

先了解一下什么是 逆序对：

例如：5 2 1，5 分别可以和 2 和 1 构成逆序对：5 2、5 1。2 可以和 1 构成逆序对 2 1。

对于这题，我们依然是将数列分为两个区间：

逆序对出现的位置有 三种情况 ：

蓝色逆序对：左半边区间的逆序对数量，区间：[l, mid]
紫色逆序对：右半边区间的逆序对数量，区间：[mid + 1, r]
红色逆序对：存在于左右半边区间之间，区间不固定

那么，如何快速准确计算出 红色逆序对 的数目？我们需要进行推导：

假设：s1 是序列中，能和 s1 对应位置构成逆序对的数目。

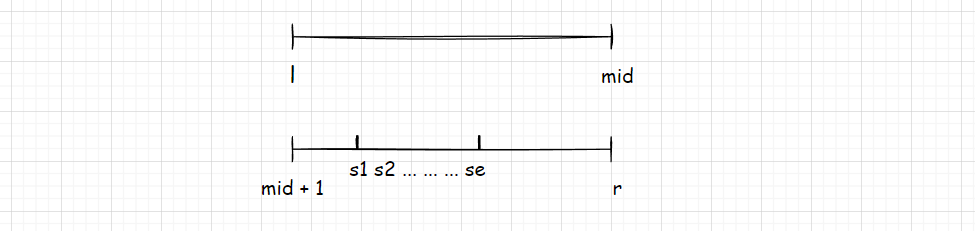
s2 ~ se 的性质和 s1 完全相同，那么对于一整个序列中，逆序对总数就是：s1 + s2 + ... + se

有了这个铺垫，我们继续推导，现在假设区间由于归并排序的原因使 [l, mid] 和 [mid + 1, r] 相对有序：

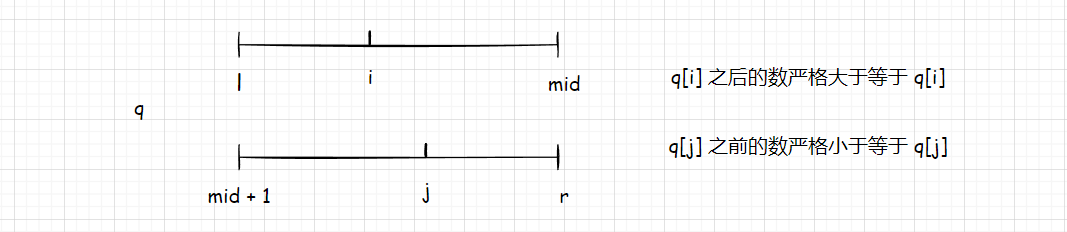
当 q[i] > q[j] 那么在 i 所在区间中 q[i] 后的数是严格大于等于 q[i] 的，j 所在区间中 q[j] 前的数是严格小于等于 q[j] 的。

一旦满足 q[i] > q[j] 这个条件，那么 q[i] 之后的元素都可以和 q[j] 构成 逆序对 。

那么它们之间 逆序对的个数 如何计算？

mid 是左区间边界，i 是满足组成逆序对数据的起始位置，那么从 i 开始一共有 mid - i + 1 个元素可以和 q[j] 构成逆序对。

有了这个公式，那么我们只需要在归并的过程中，一旦条件满足左区间元素大于右区间元素，那么从左区间的该位置开始到右区间的位置均可以构成逆序对，随后进行统计就可以。

注意：

当序列完全逆序时，所能构成的逆序对最多。

假设序列为：n, n - 1, n - 2, ..., 1，一共 n 个数

逆序对的总数就为 n - 1 + n - 2 + ... + 1，由于一个数只能与其之后的数构成逆序对，所以 1 后无元素，无法构成逆序对，等差数列为 n - 1 个数。

根据等差数列求和公式求出逆序对的计算公式：n * (n - 1) / 2，

题目给定最大数据为 100000，带入结果为 4,999,950,000，而 int 最大容纳数据为 23亿多，这里有靠近 50 亿，所以定义逆序对的变量时，需要使用 long long。

接下来我们看看代码怎么写：

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int q[N], tmp[N], n;

long long merge_sort(int q[], int l, int r)
{
    if (l >= r) return 0;
    
    int mid = l + r >> 1;
    
    // 左区间逆序对数目 + 右区间逆序对数目
    long long res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    // 归并过程 
    while (i <= mid && j <= r)
    {
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else // q[i] > q[j]
        {
            res += mid - i + 1;
            tmp[k++] = q[j++];
        }
    }
    
    // 倒入 tmp 中
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    
    // 倒回 原数组
    for (int i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
    return res;
}

int main()
{
    cin >> n;
    
    for (int i = 0; i < n; i++) cin >> q[i];
    
    cout << merge_sort(q, 0, n - 1);
    
    return 0;
}