堆与一维数组

建立堆与一维数组的联系

堆排序并不是直接对堆节点Node类型排序，而是通过建立索引之间的关系，对一维数组排序。
称之为堆排序，是因为节点索引值之间的关系与完全二叉树的非常类似，而树又称堆。
设根节点为i，i从0开始记，则：

左孩子：2i+1
右孩子：2i+2

也就是说，如果要交换根节点和左孩子的数据，就是将int[i]与int[2i+1]交换（当数据为int型时）。
这一关系是由“堆是一个完全二叉树”决定的。
堆排序的思路就是，在堆的根节点与左右孩子之间排序，然后递归地分别对左右孩子对应的子树实行相同的排序。
与冒泡、选择、插入排序的区别在于：

冒泡、选择、插入都是相邻项间进行比较，n个元素有n-1个空位，会比较n-1次。
堆排序的根节点和右孩子之间的差值为i+2，并且间隔随i增大而增大，可以显著减少比较次数。

在排序的规则上，有大顶堆和小顶堆两种：

大顶堆：将最大值放到堆顶
小顶堆：将最小值放到堆顶。

在冒泡、选择、插入排序中，我们无法通过一轮比较保证全局有序，是因为每轮比较的对象只有相邻两项，只能保证局部有序。
在堆排序中，同样无法通过一轮比较保证全局有序，单次只能在子树的根节点和左右孩子三个元素之间局部有序。
堆排序的步骤为（以大顶堆为例）：

递归地选出局部最大值，当整个数组局部排序完成后，根节点下标为[0]的根节点元素即为全局最大值。
将全局最大值与数组最后一个元素交换位置。
忽略数组最后一个元素，重复第1步，将新的全局最大值与倒数第二个元素交换位置。
如此反复，得到有序序列。

对比冒泡排序，可以发现，堆排序与冒泡排序非常类似，都是选出全局最大值，然后将全局最大值加入到有序序列。
不同之处在于冒泡排序是相邻元素间两两比较，而堆排序有较大的空隙，减少了比较次数，从而优化时间复杂度。

局部最大值

假设有一个待排序的数组：int nums[] = { 2,5,4,1,3,7,6 };
我们可以拆成如下几个堆：

[2,5,4]
[5,1,3]
[4,7,6]

首先定义堆内的排序方法，这一步会被反复调用，我们可以单独拿出来，封装成一个函数。

//传入数组、根节点索引、无序序列长度
void adjust(int num[], int index, int n) {
    //j默认指向左孩子
    int j = 2 * index;
    if (j < n && num[j - 1] < num[j]) {
        //j指向左右孩子中的较大值
        j++;
    }
    //将较大值移到根节点位置
    if (num[index - 1] < num[j - 1]) {
        int tmp = num[index - 1];
        num[index - 1] = num[j - 1];
        num[j - 1] = tmp;
    }
}

这一方法只能在三个元素间选出较大值，子树的叶子节点的值可能比根节点还要大。

如果我们对红框内的子树排序完成之后，再对紫框进行排序，那么根节点4的左右孩子都将比根节点要大，我们还需要回头对红框进行一次排序。那么第一趟对红框的排序就显得很多余。
因此，我们实际的排序方式是自下而上。

建堆

掌握了局部最大值，我们就可以对一个线性数组进行堆排序了。
需要注意的是，堆排序仍然是对线性序列的排序，我们称这一算法为堆排序，是因为这一过程中，元素索引值之间的关系与完全二叉树非常类似。
前面已经说过，下标从0开始的排序需要回头再排一趟，因此我们选择自下而上建堆。
对于索引为i的元素，它的右孩子索引为2*i+1，我们需要保证它小于等于元素个数n，则有2*i+1<=n。
化简得到：i<=(n-1)/2，由于结果为整型，1/2会丢失，所以i<=n/2，此即为计数器的初始值。
由于这里我们控制的是索引，从1开始，所以计数器控制条件为i>=0。

朴实无华的建堆

int main() {
	int num[] = { 2,4,3,6,7,5,1 };
	int length = sizeof(num) / sizeof(num[0]);
	//建树
	for (int i = length/2; i >= 1; i--) {
		adjust(num, i, length);
	}
	//检验结果
	for (int i = 0; i < length; i++) {
		printf("%d ", num[i]);
	}
	return 0;
}

观察输出，我们会发现，一趟下来的结果并不是完全有序的。
与冒泡排序类似，我们每趟比较只能在三个元素间确定最大值，与兄弟节点向双亲节点传递最大值。
这样会导致部分元素虽然比较大，但因为不是当前子堆中最大的，而没有被向上传递。
这个问题在冒泡排序中也存在，冒泡排序的做法是多来几趟循环。在堆排序中，我们可以改进局部最大值的adjust()方法，递归地使得子树有序。

void adjust(int num[], int index, int n) {
	//向上覆盖会导致数据丢失，需要临时变量存储
	int tmp = num[index - 1];
	//j默认指向左孩子
	int j = 2 * index;
	while (j <= n) {
		if (j < n && num[j - 1] < num[j]) {
			//指向左右孩子中的较大值
			j++;
		}
		if (tmp >= num[j - 1]) {
			//当前的根节点已是最大元素，不需要交换
			break;
		}
		//将较大值向上覆盖
		//左右孩子的较大值赋值给双亲结点
		num[j / 2 - 1] = num[j - 1];
		//调整指针位置，指向该孩子的左孩子
		j = 2 * j;
	}
	//将num中第index个元素放到最终调整的位置上。
	num[j / 2 - 1] = tmp;
}

交换-调整

在adjust()方法中，我们并没有对左右子树的位置进行调整，只能保证根节点大于左右孩子。
在建堆的过程中，我们也无法保证最后的结果是有序的，只能保证根节点大于它的左右孩子，而无法保证左右孩子间有序。

交换指的是将目前排出的最大值与数组最后一个元素交换位置。
调整指的是将交换后的剩余元素从上而下调整为一个新的大顶堆。

for (int i = length - 1; i >= 0; i--) {
    //交换
    int tmp = num[i];
    num[i] = num[0];
    num[0] = tmp;
    //调整
    adjust(num, 1, i);
}

在这一步的调整中，我们仍然调用了adjust()方法，并且在方法参数中，修改的值只有数组的右边界n。
而在建堆过程中，我们是自下而上，进行了多次调整。
原因是adjust()方法的实现中，之能在一条线上调整，本质还是数组的移动。与在数组中插入元素后，普通的移动数据不同：

普通的数组移动是相邻元素向后覆盖。
堆排序的元素移动是满足完全二叉树下标索引关系的元素间向上覆盖。

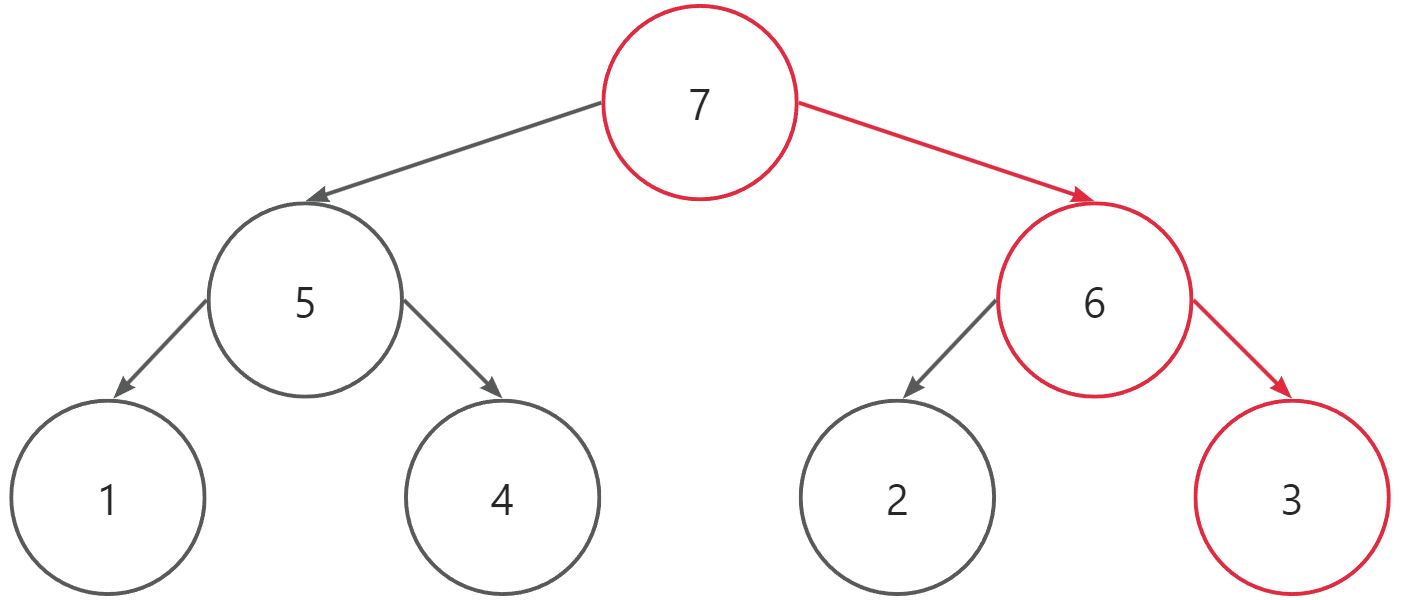
也就是说，只能保证一条线上局部有序。
并且观察adjust()方法，可以发现它只对左右孩子中的较大值进行调整。如果自上而下建堆，那么无论循环多少次，较小值对应的子树都无法有效排序。因此在建堆的过程中，我们选择自下而上的方法，保证每一个根节点一定大于它的左右孩子。
在交换调整的过程中，原数组的末尾元素被调整到整个堆的根节点位置，它一定小于左右孩子，将在adjust()方法内移动到一个合适的位置。在移动的过程中，会将较大值向上移动，使得新树仍然有序。

总结概括

堆排序是对线性序列的排序，而不是真的对一个完全二叉树进行排序，用完全二叉树的形式解释堆排序的过程是出于直观的需要。

#include <stdio.h>
//传入数组、根节点索引、无序序列长度
void adjust(int num[], int index, int n);
int main() {
	int num[] = { 2,4,3,6,7,5,1 };
	int length = sizeof(num) / sizeof(num[0]);
	//建树
	for (int i = length / 2; i >= 1; i--) {
		adjust(num, i, length);
	}
	for (int i = length - 1; i >= 0; i--) {
		//交换
		int tmp = num[i];
		num[i] = num[0];
		num[0] = tmp;
		//调整
		adjust(num, 1, i);
	}
	//检验结果
	for (int i = 0; i < length; i++) {
		printf("%d ", num[i]);
	}
	return 0;
}

void adjust(int num[], int index, int n) {
	//向上覆盖会导致数据丢失，需要临时变量存储
	int tmp = num[index - 1];
	//j默认指向左孩子
	int j = 2 * index;
	while (j <= n) {
		if (j < n && num[j - 1] < num[j]) {
			//指向左右孩子中的较大值
			j++;
		}
		if (tmp >= num[j - 1]) {
			//当前的根节点已是最大元素，不需要交换
			break;
		}
		//将较大值向上覆盖
		//左右孩子的较大值赋值给双亲结点
		num[j / 2 - 1] = num[j - 1];
		//调整指针位置，指向该孩子的左孩子
		j = 2 * j;
	}
	//将num中第index个元素放到最终调整的位置上。
	num[j / 2 - 1] = tmp;
}