算法详解
多路归并;多路归并算法从理论到应用(易懂)_留恋单行路的博客-CSDN博客
多路归并就是将多个已经归并排序排好序的数组再进行排序(不一定是通过归并排序)。
算法题目

这道题就是一般做法是先通过排序将三个数组排好然后再进行三指针求最小。但是我们仔细考虑一下,如果我们先将这三个数组排好序那么势必需要额外开一个数组,那么空间复杂度就变成了O(N)。如果我们在排序的同时去取最小距离呢?我们就不需要开一个额外的数组了。 但是那样咋做呢?我们来模拟一下吧。
假如现在我们已经找到三个点了,分别是a,b,c;那么我们如何求例题中那个式子的最小值呢?其实我们可以将例题中的式子换一下。就变成了len = 2 * (max(a,b,c) - min(a,b,c)).如下图
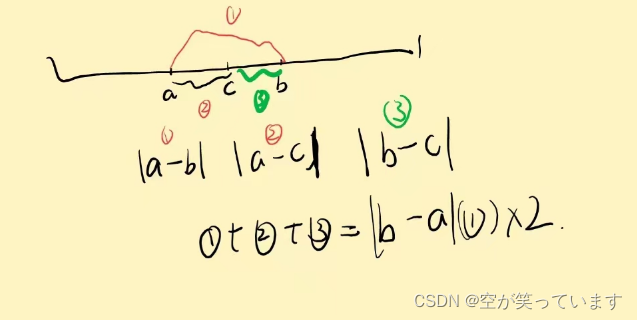
然后,继续:那么我们如何才能找到那三个指针呢?我认为只需要三个指针每次如果谁小于等于其他两个指针就算一次res(式子的值)=(max - min)*2。然后将最小的那个指针向后移动(目的:减小三个指针之间的值)。
#include <iostream>
using namespace std;const int N = 100010;
long long int a[N];
long long int b[N];
long long int c[N];int main(){
long long int l,n,m;
cin>>l>>n>>m;
for(int i=0;i<l;i++)cin>>a[i];
for(int i=0;i<n;i++)cin>>b[i];
for(int i=0;i<m;i++)cin>>c[i];
long long int res = 1e18;
int i,j,k;
long long int x,y,z;
for( i=0,j=0,k=0;i<l&&j<n&&k<m;){
x=a[i], y=b[j], z=c[k];
res = min(res,max(x,max(y,z)) - min(x,min(y,z)));
if(x<=y&&x<=z) i++;
else if(y<=x&&y<=z) j++;
else k++;
}
cout<<res*2;
return 0;
}