1.简述
小波去噪滤波算法是一种基于小波变换的滤波方法,它通过对信号进行小波变换来分解信号的频率分量,并根据信号的特点选择合适的阈值处理方法来去除噪声。该算法的主要思想是将信号分解成多个频率分量,根据信号的特点选择合适的阈值处理方法对每个频率分量进行去噪处理,然后将去噪后的频率分量进行合成,得到平滑后的信号。 具体来说,小波去噪滤波算法的步骤如下:
- 对信号进行小波分解,得到多个频率分量。
- 对每个频率分量进行阈值处理,去除噪声。
- 将去噪后的频率分量进行合成,得到平滑后的信号。小波去噪滤波算法的优点是可以有效地去除噪声,同时保留信号的整体趋势;缺点是需要选择合适的小波基和阈值处理方法,否则可能会影响滤波的效果。另外,小波去噪滤波算法对于信号中存在的快速变化的特征可以得到很好的保留,因此在一些需要保留信号快速变化特征的应用场景中,小波去噪滤波算法得到了广泛的应用。
2.代码及运行结果
小波除噪实例:
load sinsin %打开原始图像
%% X中包含图像信息
init=2055615866;
randn('seed',init);
x=X+18*randn(size(X)); %叠加后产生噪声图像
%% 用wdencmp函数给图像除噪 使用全局阈值参数除噪
[thr,sorh,keepapp]=ddencmp('den','wv',x);
xd=wdencmp('gbl',x,'sym4',2,thr,sorh,keepapp);
%% 显示
subplot(121)
imshow(x,map)
title('加噪图像')
subplot(122)
imshow(xd,map)
title('除噪图像')

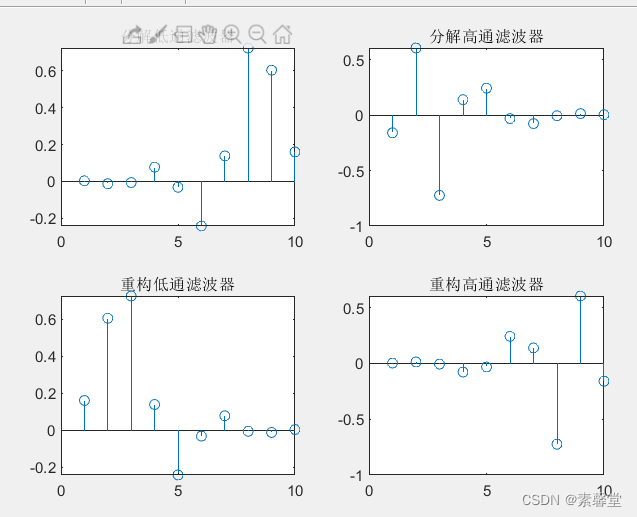
小波滤波器设计 分解和重构的滤波器
wname='db5'; %设置小波名
[Lo_D,Hi_D,Lo_R,Hi_R]=wfilters(wname);
%% 计算与给定小波名相关的四个滤波器
subplot(221);stem(Lo_D);
title('分解低通滤波器');
subplot(222);stem(Hi_D);
title('分解高通滤波器');
subplot(223);stem(Lo_R);
title('重构低通滤波器');
subplot(224);stem(Hi_R);
title('重构高通滤波器');
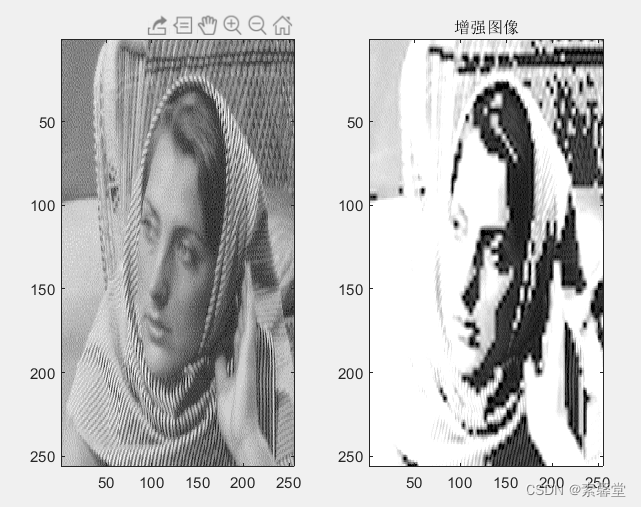
小波增强
load woman;
subplot(121);
image(X);
colormap(map);
title('原始图像');
[c,s]=wavedec2(X,2,'sym4');
%% 进行二层小波分解
len=length(c); %处理分解系数,突出轮廓,弱化细节
for I=1:len
if(c(I)>350)
c(I)=2*c(I);
else
c(I)=0.5*c(I);
end
end
nx=waverec2(c,s,'sym4'); %分解系数重构
%% 画出增强图像
subplot(122);
image(nx);
title('增强图像')