什么是递归？

函数直接或间接调用自身的过程称为递归，相应的函数称为递归函数。使用递归算法，某些问题可以很容易地解决。这样的问题的示例是河内塔（TOH）、中序/前序/后序树遍历、图的DFS等。递归函数通过调用自身的副本并解决原始问题的较小子问题来解决特定问题。在需要时可以生成更多的递归调用。我们必须知道，我们应该提供一个特定的情况，以终止这个递归过程。所以我们可以说，每次函数调用自己时，都是用原始问题的更简单版本。

递归的性质：

• 使用不同的输入多次执行相同的操作。
• 在每一步中，我们尝试更小的输入，使问题更小。
• 需要基本条件来停止递归，否则将发生无限循环。

算法：步骤

在函数中实现递归的算法步骤如下：

• 步骤1-定义基本案例：找出已知解或解不重要的最简单的情况。这是递归的停止条件，因为它防止函数无限地调用自己。
• 步骤2-定义递归用例：用更小的子问题来定义问题。将问题分解为更小的问题，并递归调用函数来解决每个子问题。
• 步骤3-确保递归终止：确保递归函数最终达到基本情况，并且不会进入无限循环。
• 步骤4-联合收割机解决方案：将子问题的解组合起来求解原问题。

数学解释

让我们考虑一个问题，程序员必须确定前n个自然数的总和，有几种方法可以做到这一点，但最简单的方法是简单地将从1到n的数字相加。这个函数看起来像这样

方法（1）-简单地逐个添加

f(n) = 1 + 2 + 3 +...+ n

但是有另一种数学方法来表示它，

方法（2）-递归加法

f(n) = 1             n=1
f(n) = n + f(n-1)    n>1

方法（1）和方法（2）之间有一个简单的区别，在方法（2）中，函数“f（）”本身在函数内部被调用，因此这种现象被称为递归，包含递归的函数被称为递归函数，最后，这是程序员手中的一个很好的工具，可以更容易和有效地编码一些问题。

递归函数如何存储在内存中？

递归使用更多的内存，因为递归函数在每次递归调用时都会添加到堆栈中，并将值保留在那里，直到调用完成。递归函数使用LIFO（LAST IN FIRST OUT）结构，就像堆栈数据结构一样。

如何在递归中将内存分配给不同的函数调用？

当从main（）调用任何函数时，内存在堆栈上分配给它。递归函数调用自身，被调用函数的内存分配在分配给调用函数的内存之上，并且为每个函数调用创建局部变量的不同副本。当达到基本情况时，函数将其值返回给调用它的函数，并且内存被释放，并且过程继续。

def printFun(test):

	if (test < 1):
		return
	else:

		print(test, end=" ")
		printFun(test-1) # statement 2
		print(test, end=" ")
		return

# Driver Code
test = 3
printFun(test)

输出：

3 2 1 1 2 3 

时间复杂度：O（1）
空间复杂度：O（1）

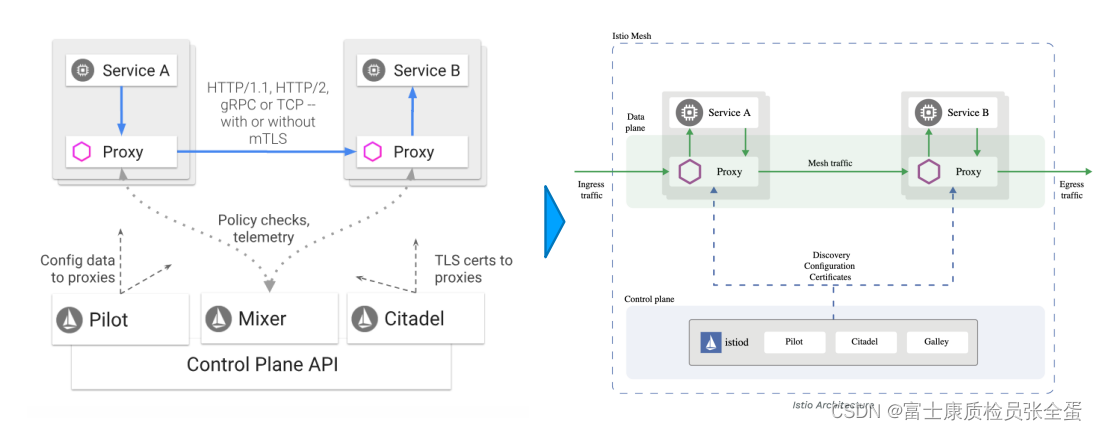
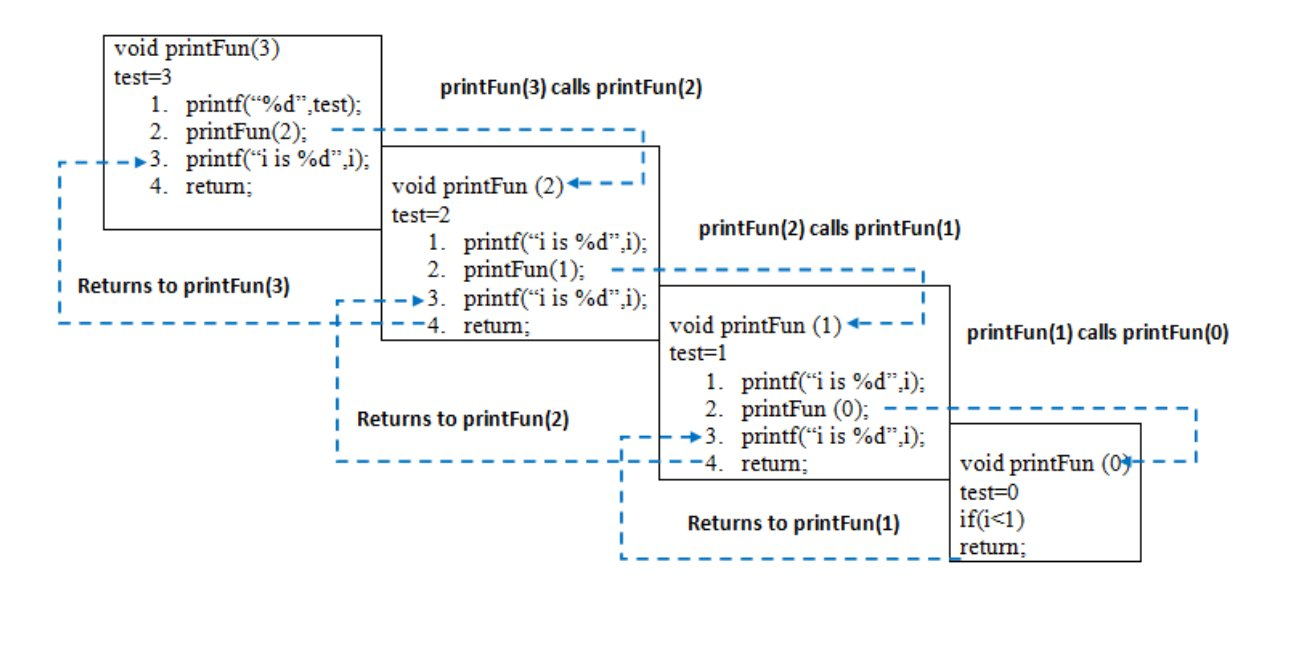
当从main（）调用printFun（3）时，内存被分配给printFun（3），局部变量test被初始化为3，语句1到4被压入堆栈，如下图所示。它首先打印“3”。在语句2中，调用printFun（2），并将存储器分配给printFun（2），并将局部变量test初始化为2，并将语句1至4推入堆栈。类似地，printFun（2）调用printFun（1），printFun（1）调用printFun（0）。printFun（0）转到if语句，并返回printFun（1）。执行printFun（1）的其余语句，并返回printFun（2），依此类推。在输出中，打印从3到1的值，然后打印1到3。内存堆栈如下图所示。

现在，让我们讨论几个可以用递归解决的实际问题，并了解它的基本工作原理。如需基本了解，请阅读以下文章。

问题1：写一个程序和递归关系，找到n的斐波那契级数，其中n>2。

数学方程：
n if n == 0, n == 1;      
fib(n) = fib(n-1) + fib(n-2) otherwise;

相互关系：
T(n) = T(n-1) + T(n-2) + O(1)

递归程序：
输入：n = 5 
输出：
斐波那契数列的5个数是：0 1 1 2 3

# Function for fibonacci
def fib(n):

	# Stop condition
	if (n == 0):
		return 0

	# Stop condition
	if (n == 1 or n == 2):
		return 1

	# Recursion function
	else:
		return (fib(n - 1) + fib(n - 2))

# Driver Code

# Initialize variable n.
n = 5;
print("斐波那契数列的5个数是:",end=" ")

# for loop to print the fibonacci series.
for i in range(0,n):
	print(fib(i),end=" ")

时间复杂度：O（2^n）
空间复杂度：O（n）

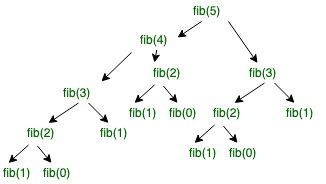
这里是输入5的递归树，它清晰地展示了如何将一个大问题分解成更小的问题。
fib（n）是一个Fibonacci函数。给定程序的时间复杂度可以取决于函数调用。

fib(n) -> level CBT (UB) -> 2^n-1 nodes -> 2^n function call -> 2^n*O(1) -> T(n) = O(2^n)

最好的情况：

T(n) = θ(2^n\2)

问题2：编写一个程序和递归关系，找到n的阶乘，其中n>2。

数学方程：
1 if n == 0 or n == 1;      
f(n) = n*f(n-1) if n> 1;

相互关系：
T(n) = 1 for n = 0
T(n) = 1 + T(n-1) for n > 0

输入：n = 5
输出：
5的阶乘是：120

# Factorial function
def f(n):

	# Stop condition
	if (n == 0 or n == 1):
		return 1;

	# Recursive condition
	else:
		return n * f(n - 1);


# Driver code
if __name__=='__main__':

	n = 5;
	print("factorial of",n,"is:",f(n))

时间复杂度：O（n）
空间复杂度：O（n）

实例：递归在实际问题中的真实的应用

递归是一种强大的技术，在计算机科学和编程中有许多应用。以下是递归的一些常见应用：

• 树和图遍历：递归经常用于遍历和搜索数据结构，如树和图。递归算法可以用于以系统的方式探索树或图的所有节点或顶点。
• 排序算法：递归算法也用于排序算法，如快速排序和归并排序。这些算法使用递归将数据划分为更小的子数组或子列表，对它们进行排序，然后将它们合并在一起。
• 分治算法：许多使用分治方法的算法，如二分查找算法，使用递归将问题分解为更小的子问题。
• 分形生成：可以使用递归算法来生成分形形状和图案。例如，曼德尔布罗特集是通过将递归公式重复应用于复数而生成的。
• 回溯算法：回溯算法用于解决涉及做出一系列决策的问题，其中每个决策都取决于先前的决策。这些算法可以使用递归来实现，以探索所有可能的路径，并在未找到解决方案时进行回溯。
• 记忆化：记忆是一种技术，涉及存储昂贵的函数调用的结果，并在再次发生相同的输入时返回缓存的结果。记忆可以使用递归函数来实现，以计算和缓存子问题的结果。

这些只是递归在计算机科学和编程中的许多应用中的几个例子。递归是一种通用且功能强大的工具，可用于解决许多不同类型的问题。

说明：递归的一个真实的例子

递归是一种涉及函数调用自身的编程技术。它可以成为解决复杂问题的强大工具，但也需要仔细实现，以避免无限循环和堆栈溢出。

def factorial(n):
	# Base case: if n is 0 or 1, return 1
	if n == 0 or n == 1:
		return 1

	# Recursive case: if n is greater than 1, call the function with n-1 and multiply by n
	else:
		return n * factorial(n-1)

# Call the factorial function and print the result
result = factorial(5)
print(result) # Output: 120

在这个例子中，我们定义了一个名为factorial的函数，它接受整数n作为输入。该函数使用递归来计算n的阶乘（即，直到n的所有正整数的乘积）。
阶乘函数首先检查n是0还是1，这是基本情况。如果n为0或1，则函数返回1，因为0！1！都是1。
如果n大于1，则函数进入递归情况。它以n-1作为参数调用自身，并将结果乘以n。计算n！通过递归计算（n-1）！.
需要注意的是，如果不小心使用，递归可能效率低下，并导致堆栈溢出。每个函数调用都会向调用堆栈添加一个新帧，如果递归太深，则会导致堆栈变得太大。此外，递归会使代码更难理解和调试，因为它需要考虑多个级别的函数调用。
然而，递归也可以是解决复杂问题的强大工具，特别是那些涉及将问题分解为更小的子问题的问题。如果使用正确，递归可以使代码更优雅，更容易阅读。

递归VS迭代

递归：

• 当基本情况变为true时终止。
• 用于函数。
• 每个递归调用都需要堆栈内存中的额外空间。
• 更小的代码大小。

迭代：

• 当条件变为false时终止。
• 用于循环。
• 每次迭代都不需要任何额外的空间。

递归编程相对于迭代编程的缺点是什么？

注意，递归和迭代程序具有相同的问题解决能力，即，每个递归程序都可以迭代地编写，反之亦然。递归程序比迭代程序具有更大的空间需求，因为所有函数将保留在堆栈中，直到达到基本情况。由于函数调用和返回的开销，它也有更大的时间需求。
此外，由于代码的长度较小，代码难以理解，因此在编写代码时必须格外小心。如果没有正确检查递归调用，计算机可能会耗尽内存。

递归编程比迭代编程有什么优势？

递归为编写代码提供了一种干净而简单的方法。有些问题本质上是递归的，如树遍历，河内塔等。对于这样的问题，最好编写递归代码。我们也可以在堆栈数据结构的帮助下迭代地编写这样的代码。例如，参考无递归的中序树遍历，迭代河内塔。