引言：

在计算机科学中，有一种强大的概念叫做递归。它可以帮助我们解决各种复杂的问题，使代码更加简洁而优雅。递归是一种函数调用自身的技术，通过将问题分解成较小的子问题，以及逐步将其解决，从而达到解决整个问题的目的。在本文中，我们将深入探讨递归的原理、应用场景，以及注意事项。

一. 递归的基本原理

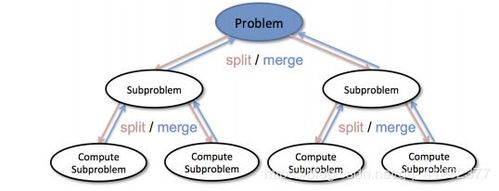
递归是一种函数调用自身的技术。通过将一个问题分解为较小的子问题，并逐步解决这些子问题，递归能够解决复杂的问题。递归的基本原理包括三个要素：递归终止条件、问题的拆分和逐步解决、以及自身调用。

1. 递归终止条件：
递归终止条件是指当满足某个条件时，递归不再继续进行，而是直接返回结果。这个条件通常是事先定义好的边界条件，一般是问题规模达到一个足够小的状态时，可以直接解决出结果。没有递归终止条件或者终止条件不正确，递归可能会陷入无限循环，导致程序崩溃。

2. 问题的拆分和逐步解决：
递归的核心思想是将一个大问题分解成较小的子问题，并通过同样的方法解决这些子问题。通过将问题不断细分，直到达到递归终止条件，然后逐步解决子问题，最终得到整个问题的解。每次递归调用都会将问题规模缩小，直到达到递归终止条件为止。

3. 自身调用：
在递归中，函数会调用自身来处理子问题。通过函数调用自身来解决子问题，实现了问题的分解和逐步解决。递归调用的过程中，每次调用都会有自己独立的变量和执行环境，这样可以保证每个子问题都能得到正确的解答。

总结：
递归的基本原理包括递归终止条件、问题的拆分和逐步解决、以及自身调用。递归终止条件指明递归何时结束，问题的拆分和逐步解决使得大问题变得可解，而自身调用则实现了问题的分解和逐步求解的过程。理解递归的基本原理是使用递归解决问题的关键，正确定义递归终止条件和合理划分子问题可以确保递归算法的正确性和效率。

二. 递归的应用场景

递归在计算机科学中有广泛的应用，下面详细介绍几个常见的应用场景：

1. 排列组合问题：
递归可以用于解决排列组合问题，如计算一组元素的全排列或组合。通过不断将问题分解为较小的子问题，递归可以枚举所有可能的排列或组合。例如，给定一个数组，可以通过递归生成所有可能的子集或其中元素的排列。

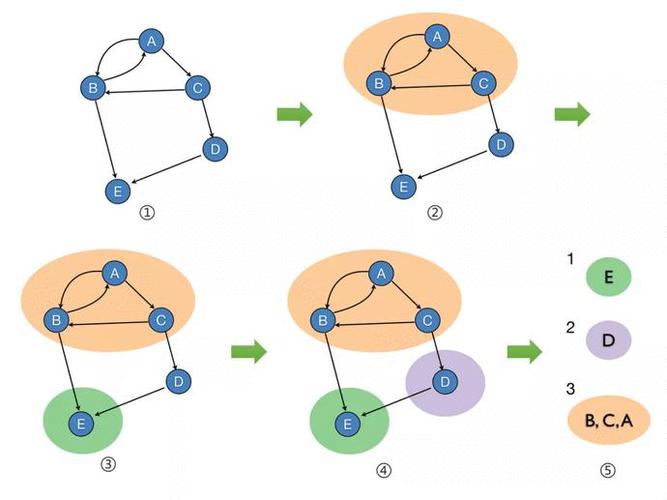
2. 树和图的遍历：
递归算法在树和图的遍历中有广泛的应用。深度优先搜索（DFS）和广度优先搜索（BFS）是常见的遍历算法，它们可以通过递归方式实现。递归地访问节点和它们的邻居，从而可以遍历整个树或图的节点。

3. 分治算法：
分治算法是一种通过将问题分解为较小的子问题来解决整体问题的方法。递归可以用于实现分治算法。例如，对于排序问题，可以通过将数组分成两半，并递归地对每个子数组进行排序，然后将排序好的子数组合并起来，从而实现归并排序。

4. 数学问题：
递归在解决数学问题时也很有用。例如，斐波那契数列是一个经典的递归问题，每个数都是前两个数之和。通过递归计算前两个数之和，可以得到斐波那契数列的任意项。另外，递归还可以用于计算阶乘等数学运算。

5. 文件和目录的遍历：
在文件系统中，递归可以用于遍历文件目录树。通过递归访问文件夹中的所有子文件夹和文件，可以实现对整个文件系统的遍历和操作。

需要注意的是，在使用递归时要确保递归终止条件的正确性，以避免无限递归。此外，递归的性能较低，因为每次递归调用都需要消耗额外的栈空间。在处理大规模问题时，可以考虑使用迭代方法进行优化。

三. 递归的优点和缺点

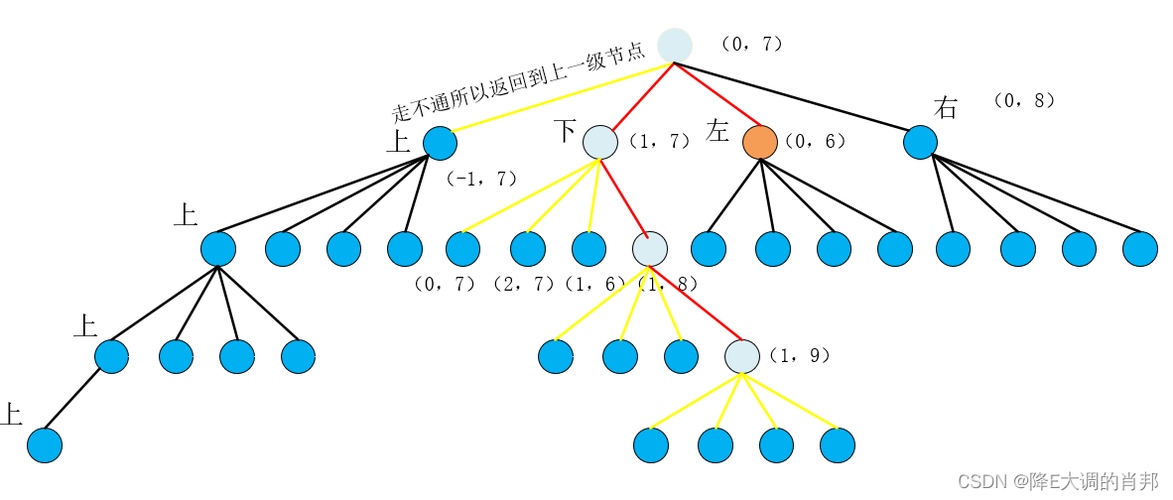
递归作为一种强大的编程技巧，具有以下优点和缺点：

优点：

1. 代码简洁而优雅：递归的实现通常更加简洁，容易理解和实现。递归可以将复杂的问题分解为较小的子问题，使得代码更加直观和易读。

2. 解决复杂问题：递归提供了一种简单且直观的思考方式，可以解决一些复杂的问题。通过递归的分解和逐步解决，可以有效地处理具有高度嵌套结构的问题。

3. 数学概念的结合：递归可以与数学归纳法、数学递归等数学概念相结合，更好地解决问题。这使得递归算法在数学领域的问题中特别有用。

缺点：

1. 栈空间消耗：递归调用需要消耗额外的栈空间。每次递归调用都会在栈上创建一个新的帧，这可能导致栈溢出的风险。尤其是在处理大规模问题时，栈空间的消耗可能会成为限制性因素。

2. 性能开销：递归调用的性能通常较低，相比迭代方法，时间和空间开销较大。递归需要频繁地进行函数调用和返回，这会增加额外的开销，并可能导致执行时间的增加。

3. 可能陷入无限循环：如果没有正确定义递归终止条件或者终止条件不正确，递归可能会陷入无限循环。这会导致程序永远无法终止，消耗大量的系统资源，并可能导致程序崩溃。

4. 重复计算：在某些情况下，递归算法可能会进行大量的重复计算，影响性能。这是因为递归在解决问题时可能会多次访问相同的子问题，而没有对已经计算过的结果进行记忆化或者缓存。

综上所述，递归作为一种强大的编程技巧，在解决某些问题时具有明显的优势。但同时，我们也要注意递归的缺点，合理评估递归的适用性，并根据具体问题进行选择。在使用递归时，需要注意定义递归终止条件、避免栈溢出、优化计算过程等，以提高递归算法的效率和正确性。

四. 注意事项和优化技巧

在使用递归算法时，有一些注意事项和优化技巧可以帮助提高算法的性能和正确性。下面详细介绍这些内容：

1. 定义递归终止条件：
递归必须有一个明确的终止条件，否则程序可能会陷入无限循环。在编写递归函数时，务必确保递归终止条件的正确性和完备性。终止条件应该能够使递归过程最终结束，并返回某个已知的结果。

2. 确保每次递归调用都能缩小问题规模：
在递归过程中，每次递归调用应该能够使问题规模减小，以确保问题最终能够达到递归终止条件。如果问题在递归过程中的规模没有减小，就可能陷入无限递归的循环中。

3. 避免重复计算：
在某些情况下，递归算法可能会进行大量的重复计算，影响性能。为了避免重复计算，可以利用记忆化技术或动态规划来优化递归算法。记忆化技术通过记录已经计算过的结果，以后可以直接返回，避免重复计算。动态规划则将递归过程中的子问题的解保存下来，避免重复计算。

4. 使用尾递归优化：
尾递归是一种特殊的递归形式，在递归调用的最后一步执行，且该调用的返回值直接成为当前函数的返回值，不再需要进行其他操作。一些编程语言支持尾递归优化，可以将其转化为迭代形式，提高算法的性能和效率。

5. 注意栈空间的使用：
递归调用需要消耗额外的栈空间，如果递归的层数较深或者处理大规模问题，可能导致栈溢出的风险。为了避免栈溢出，可以考虑使用迭代方式替代递归，或者使用尾递归优化。另外，在一些编程语言中，可以通过增加栈空间的限制来避免栈溢出问题。

6. 谨慎使用递归：
尽管递归是一种强大的编程技巧，但不是所有的问题都适合使用递归来解决。有时候，使用迭代或其他方式更加简单和高效。在使用递归时，需要权衡其优点和缺点，选择最适合问题的解决方法。

总结：
递归算法是一种强大的技术，但在使用时需要注意一些事项和优化技巧。定义递归终止条件、确保问题规模的减小、避免重复计算、使用尾递归优化、合理管理栈空间，并谨慎选择使用递归的问题，都是优化和提高递归算法性能的关键。

结论：

递归是一种强大的技术，能够解决各种复杂的问题，为代码提供了一种简洁而优雅的编程方式。然而，递归的正确使用需要谨慎，并且在性能方面存在一些限制。通过深入理解递归的原理、应用场景以及优化技巧，我们可以更好地利用递归算法解决问题，提高代码的效率和可读性。