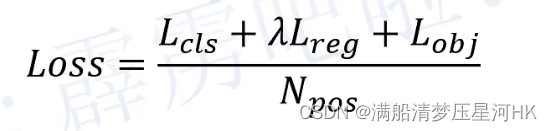【paper】 Analogical Inference for Multi-relational Embeddings
【简介】 本文是卡耐基梅隆大学的中国学者发表在 ICML 2017 上的工作，提出了 ANALOGY 模型，用于建模实体和关系的推理属性。这个模型应当也算是双线性模型中比较经典的一个了，很多模型的 baseline 中都有它。核心思想就是利用矩阵的交换性约束建模平行四边形一样的类比推理属性。

背景知识

正规矩阵

ANALOGY 将关系矩阵约束为正规矩阵，由于它是 "well-behaved" linear maps。

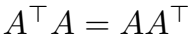
关系作为线性映射

ANALOGY 的提出不是基于 “h+r≈t” 的距离模型，而是双线性类模型的体系，且关系表示为矩阵。对于 valid 三元组 (s,r,o)(s,r,o) ，存在：头实体经过线性映射（关系）近似于尾实体。

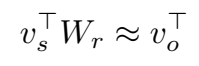
打分函数也是双线性函数：

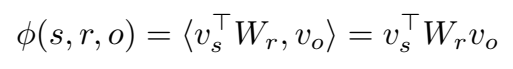
问题定义

本文解决的类比推理问题（analogical inference problem）并不是一个新问题，只是用类比推理的特性预测实体关系。

类比推理很好理解，上一个 word embedding 老生常谈的例子： man is to king as woman is to queen.

文章用平行四边形形式化描述类比推理的属性：

有 subject-relation-object 三元组：

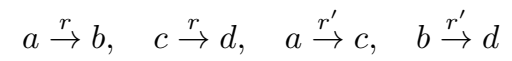
则 a、b、c、d 四个实体间存在的类比推理关系正如一个平行四边形结构：

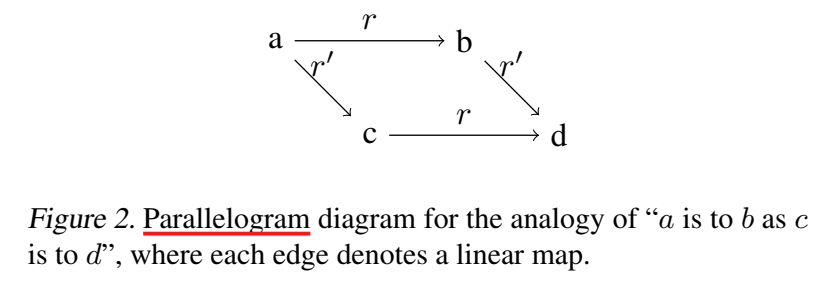
箭头只是一个直观的表示，实际上代表线性映射。

解决方案

为了建模平行四边形般的类比推理关系，线性映射（关系）需满足“交换定理（commutativity）”，即

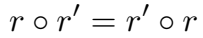
○ 代表两个关系的组合。这个很好理解，一个实体先经过关系 rr 再经过 r′r′，与它先经过 r′r′，再经过 rr，最后推理出的实体，应当是一个，也就是说两条路径是等价的。

实际中，关系的组合通常表示为关系矩阵相乘：

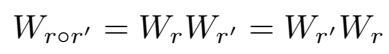
因此，ANALOGY 通过添加

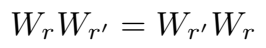
的约束建模关系的“交换等价”特性以用于类比推理。

优化目标： 对三元组作二分类，正样本标签为 +1，负样本标签为 -1

打分函数为：

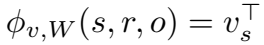
训练目标为有约束条件下的 loss 最小化：

loss 是 logistic loss：

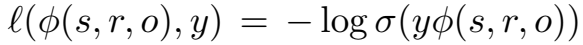
这个paper中还有好几页是定理、理论证明以及和其他双线性模型的 unified，没看。

实验

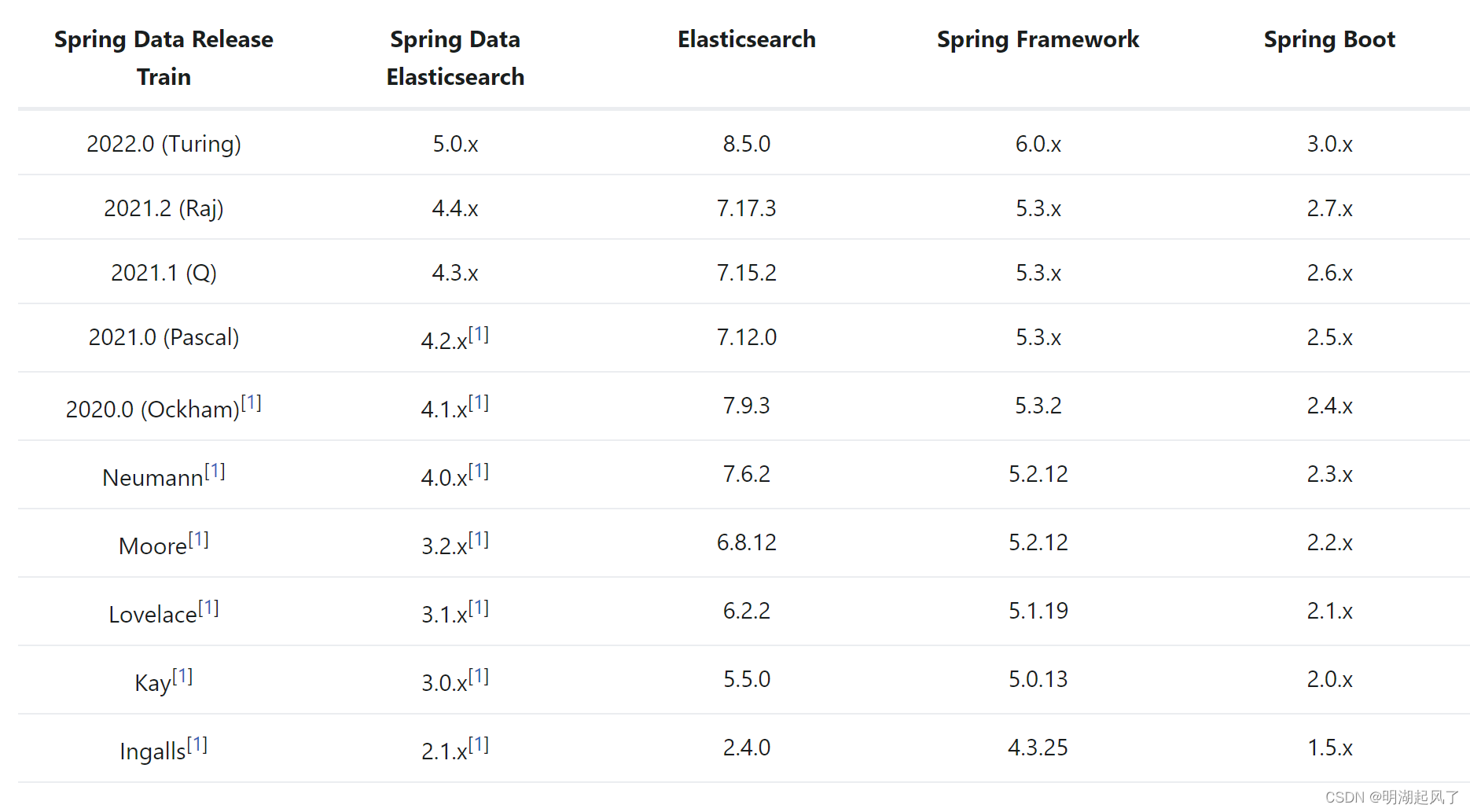
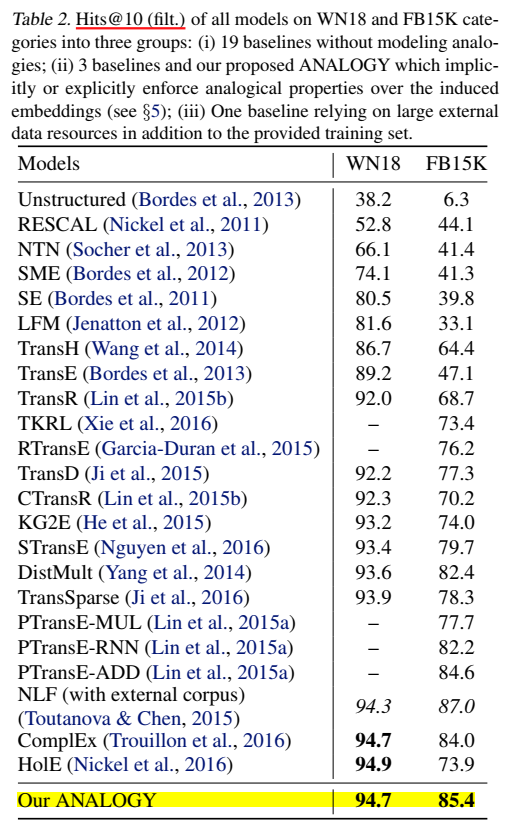
两个数据集上的 Hits@10：

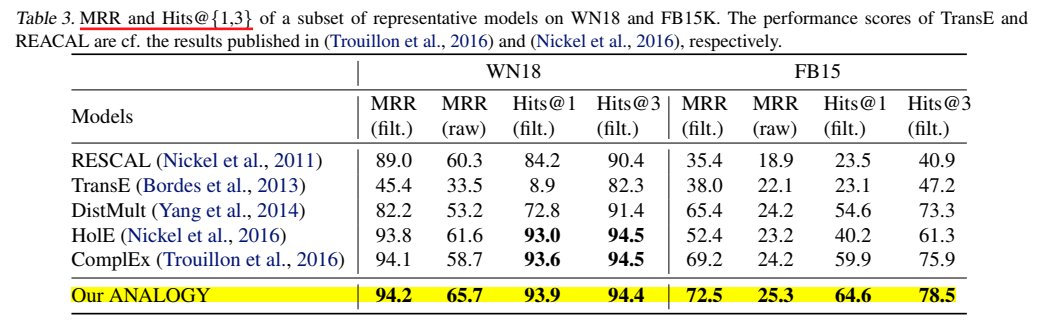
两个数据集上的 Hits@{1,3}：

【code】 GitHub - quark0/ANALOGY: Analogical inference for knowledge graph completion

 

双线性模型（五）（CP、ANALOGY、SimplE） - 胡萝不青菜 - 博客园