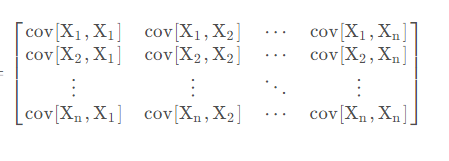目录
数学期望与方差
离散型随机变量的数学期望
注意
连续型随机变量的数学期望
方差
常用随机变量服从的分布
二项分布
正态分布
随机向量与随机变量的独立性
随机向量
随机变量的独立性
协方差
协方差的定义
协方差的意义
协方差矩阵
数学期望与方差
离散型随机变量的数学期望
离散型随机变量的数学期望是指该变量的所有可能取值乘以其对应的概率的总和。数学期望可以用以下公式表示:
E(X) = Σ(x * P(X=x))
其中,E(X)表示随机变量X的数学期望,x表示X的取值,P(X=x)表示X取值为x的概率。
换句话说,数学期望是随机变量所有可能取值的加权平均值,其中权重是对应取值的概率。

注意
对概率大的取值,该值出现的机会就大,也就是在计算取值的平均时其权重就大,因此用概率作为一种“权重”做加权计算平均值
举个栗子:
1.假设买彩票有 0.2 的概率中 500 万,0.3 的概率中 1 万,0.5 的概率中 0.1 万,
那可能的收益不可能用 500+1+0.1 来平均一下,肯定要考虑概率值
500x0.2 +1x0.3 + 0.1x0.5
2.假设有一个离散型随机变量X,其可能取值为1、2和3,对应的概率分别为0.3、0.4和0.3。那么X的数学期望可以计算如下:
E(X) = (1 * 0.3) + (2 * 0.4) + (3 * 0.3) = 0.3 + 0.8 + 0.9 = 2
所以,这个随机变量X的数学期望为2。
连续型随机变量的数学期望

对于连续型随机变量,数学期望的计算方式与离散型随机变量略有不同。数学期望仍然表示随机变量的加权平均值,但在连续型情况下,需要使用积分来进行计算。
连续型随机变量X的数学期望可以表示为:
E(X) = ∫(x * f(x)) dx
其中,E(X)表示随机变量X的数学期望,x表示X的取值,f(x)表示X的概率密度函数(PDF)。
简单来说,数学期望是随机变量X乘以其概率密度函数的积分。
举个例子,假设有一个连续型随机变量X,其概率密度函数为f(x) = 2x,其中x的取值方差范围为0到1。那么X的数学期望可以计算如下:
E(X) = ∫(x * 2x) dx
= 2 * ∫(x^2) dx
= 2 * [(x^3)/3],在0到1的范围内积分
= (1^3)/3 - (0^3)/3
= 1/3
方差
随机变量X的方差反映了X与其数学期望E(X)的偏离程度,如果X取值集中在E(X)附近,则
方差D(X)较小;如果X取值比较分散,则方差D(X)较大。
通用方差公式:

常用随机变量服从的分布

二项分布
- 伯努利概型
做了n次试验,且满足
(1) 每次试验只有两种可能结果,即A发生或A不发生
(2) n次试验是重复进行的,即A发生的概率每次均一样
(3) 每次试验是独立进行的,即每次试验A发生与否与其他次试验A发生与否是互不影响的
这种试验称为伯努利概型,或称为n重伯努利试验
例如: 将一骰子掷4次,观察出现6点的次数——4重伯努利试验
定理:在n重伯努利试验中,用p表示每次试验A发生的概率,记n次试验中事件A出现k次,则

- 二项分布
若随机变量X的分布律为

则称随机变量X服从参数为n,p的二项分布。记为X~b(n,p)
注意
- 二项分布的背景是:n重伯努利试验中事件A发生的次数X~b(n,p),其中p为一次试验中A发生的概率
- 当n=1时的二项分布X~b(1,p),又称为0-1分布(例如,扔一次硬币,观察正面朝上的次数)
正态分布
正态分布是一种连续型随机变量分布
若随机变量X的概率密度为

则称随机变量X服从参数为μ、σ^2^的正态分布,记为X~N(μ,σ^2^)。其中μ,σ(σ>0)为常数

右图可见,μ决定了图形的中心位置,当μ取不同值时,图形沿着x轴平移,而不改变其形状。
注意
自然界和生活中很多事件都服从正态分布或者近似服从正态分布的,比如人的身高、体重、收入等
随机向量与随机变量的独立性
随机向量
线性代数中,我们把标量 x 推广到向量,就是它有多个分量。
同样我们把单个随机变量可以推广到随机向量,就是它有多个分量,这样就有了随机向量的
概念了。
以二元随机向量为例:

随机变量的独立性
两个随机变量如果相互独立的话,它们的联合概率密度函数等于它们的分别的概率密度函数
乘积
推广到多个随机变量相互独立
f (x~1~, x~2~ ,.., x~n~ ) = f (x~1~) f (x~2~ )... f (x~n~ )
这和随机事件的形式上是统一的,f 换成符合 P 就可以了
注意
在实际问题中,判断两个随机变量是否相互独立,往往不是用数学定义去验证。而常常是由随机变量的实际意义去考证它们是否相互独立。如掷两枚骰子的试验中,两枚骰子出现的点数,两个彼此没有联系的工厂一天产品中各自出现的废品件数等都可以认为是相互独立的随机变量。
协方差
协方差的定义
设(X,Y)是二维随机变量(二元随机向量),称

为X与Y的协方差,记为cov(X,Y)
由定义可推导得出协方差的常用计算公式:

注意
对比方差与协方差的计算公式:
- 方差:D(X)=E(X^2^)-[E(X)]^2^,协方差:cov(X,Y)=E(XY)-E(X)E(Y)
- 随机变量X与其自身的协方差就是X的方差
协方差的意义
- 协方差反映的是X与Y之间协同发展变化的趋势
- 协方差刻画了两个随机变量之间的线性关系

协方差矩阵
对于 n 维的向量 X,它的协方差就构成了一个协方差矩阵,第一个是 X~1~ 和 X~1~ 的协方
差, 第一行第二列是 X~1~ 和 X~2~ 的协方差,第一行第 n 列是 X~1~和 X~n~ 的协方差。协方差矩阵
的对角线上是各变量的方差。