内容包括:排序的代码实现,排序原理详解,代码详解,图示
part 1:直接插入排序
代码实现:
void InsertSort(int* a, int n)
{
int i = 0;
for (i = 0; i < n - 1; i++)
{
int end = i;
int tmp = a[i + 1];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
效果图例:

![]()
排序原理:
基本原理:向一个有序区间插入一个值(此值在有序区间末尾的后一个位置)
生动些:可以将这种插入排序看作摸牌的过程,我们手上的牌都是已经按照一定顺序排列好的,现在我们又新拿了一张牌,准备插入,方法就是从手上排好的最后一张牌开始,依次比较
若是当前手上的牌大于待插入的新牌,那么需要将手上的此牌向后移动一步,腾出一个位置
若是当前手上的牌小于待插入的新牌,则新牌的位置则定下,即手上的此牌的后一个位置
代码详解:
void InsertSort(int* a, int n)
{
int i = 0;
for (i = 0; i < n - 1; i++)//所有有序区间的末尾位置
{
int end = i;//有序区间的末尾下标
int tmp = a[i + 1];//待插入的元素先保存到tmp中
while (end >= 0)//依次与有序区间中的所有元素一一比较
{
if (a[end] > tmp)
{
a[end + 1] = a[end];//有序区间的某个元素后移
end--;//继续与有序区间中的元素比较
}
else
{
break;
}
}
a[end + 1] = tmp;//待插入元素插入在有序区间某个元素的后面 or 越过整个有序区间,成为第一个
}
}
1 for循环构造出所有有序区间末尾下标的可能
2 待插入元素需要临时保存在tmp变量中,因为在插入过程中伴随着有序区间元素的后移,若是不提前保存待插入元素的值,则可能导致待插入元素被覆盖
3 若是待插入元素比有序区间的元素小,则此有序区间的元素即其后面都需要后移一位,但是比较还在继续,直至待插入元素比有序区间的元素大,才会停止比较
4 停止比较的两种可能(待插入元素确定位置的两种情况):
1 待插入元素在有序区间内找到一个比小的元素,则它需要插在此元素的后面,即end+1的位置
2 待插入元素比所有有序区间内的元素都要小,此时end=-1,比无可比,则所有有序区间内的元素都后移一位,它插在数组的第一个位置上,即end+1的位置
故而在代码中我设计:若是遇到比待插入元素小的元素直接break,这样可以统一。
part 2:希尔排序
希尔排序是直接插入排序基础之上的代码设计
代码实现:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
int i = 0;
for (i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}排序原理:
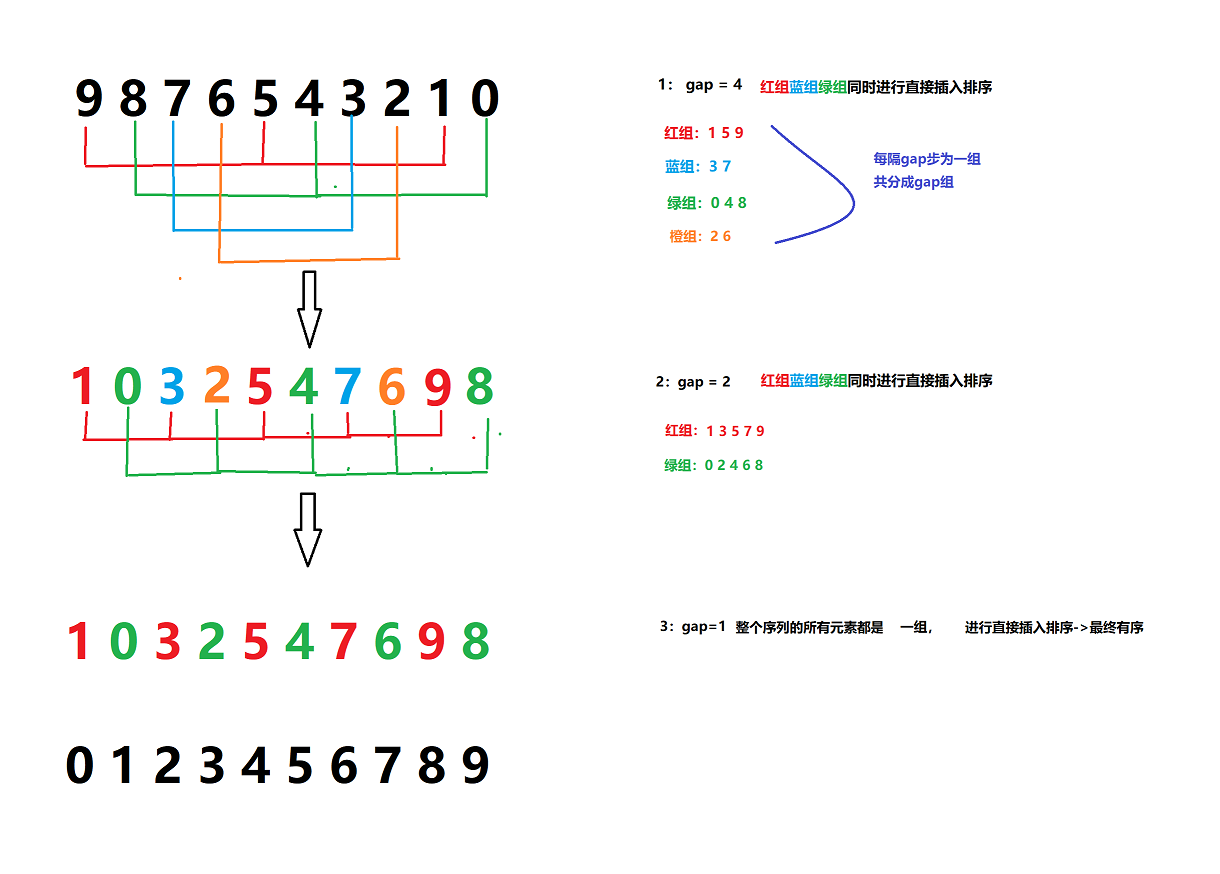
基本原理:第一步:多次预排序使得序列逼近有序(gap>1)
第二步:直接插入排序,使得序列最终有序(gap==1)
间隔gap分为一组,共又gap组
gap=gap/3+1 或者gap=gap/2 无论哪种都会使得gap最终=1,就是所有元素构成一组,此时对一组的排序就是前面所介绍的直接插入排序,会让数组最终有序
代码详解:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)//多次预排,gap=1时数组已经最终有序,结束循环
{
gap = gap / 3 + 1;//gap的变化,保证了gap的最后一次值是1
int i = 0;
for (i = 0; i < n - gap; i++)//有序区间末尾的下标,多组并排,i的变化即end的变化,end的值代表当前插入排序的是哪一组,end的取值必须<n-gap,下面有详解原因
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)//对一组的某个待排序元素进行插入排序
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;//间隔gap为一组,所以end的前一个元素是end-gap
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}下面省略每组的每个待排序元素插入自己所在组有序区间的结果,读者可自行操作,这里介绍方法

end处在红组:对红组的一个待排序元素进行插入排序,初始有序区间内只有一个9
end++,end处在绿组,对绿组的一个待排序元素进行插入排序,初始有序区间内只有一个8
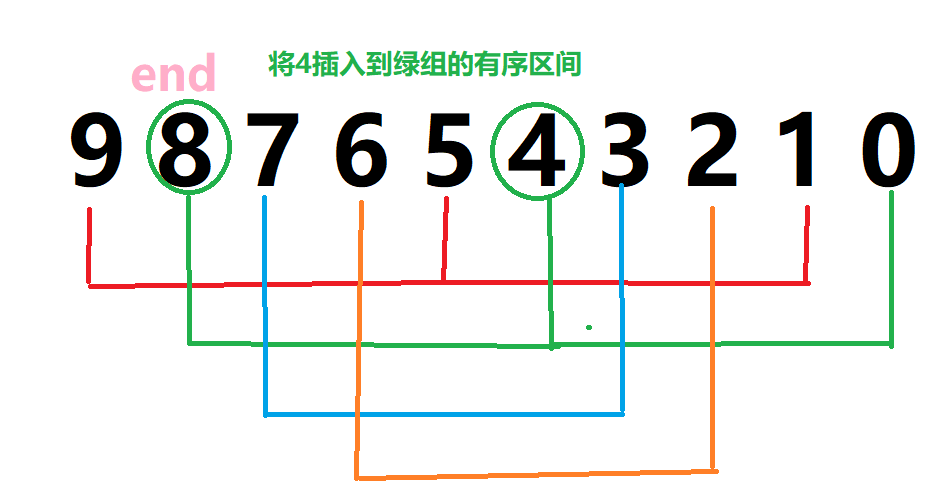
end++,end处在蓝组, 对蓝组的一个待排序元素进行插入排序,初始有序区间内只有一个7
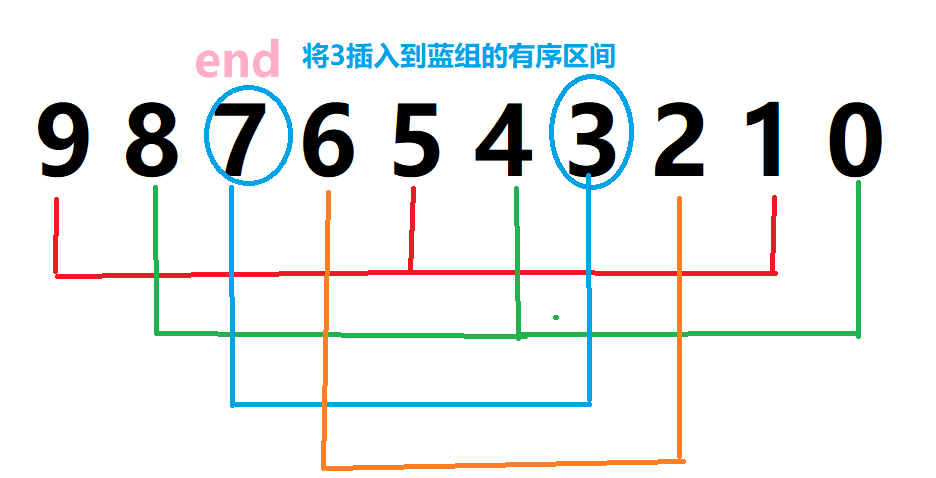
end++,end处在橙组, 对橙组的一个待排序元素进行插入排序,初始有序区间内只有一个6

之后的end继续++,先是将红组中的下一个待插入元素进行插入排序,再是对绿组的下一个待插入元素进行插入排序,然后是对蓝组的下一个待插入元素进行插入排序,再是对橙组的下一个待插入元素进行插入排序,红,绿,蓝,橙……如此循环多组并排
但是end最终只能抵达n-gap-1的位置,即,end<n-gap,因为我们的操作是将end+gap位置的待插入元素进行插入,必须保持数组的下标不越界,当end处在n-gap位置时,它的后一个元素end+gap就是n了,属于非法下标 ,而且当end抵达最终位置时,这一趟的预排序已经处理完成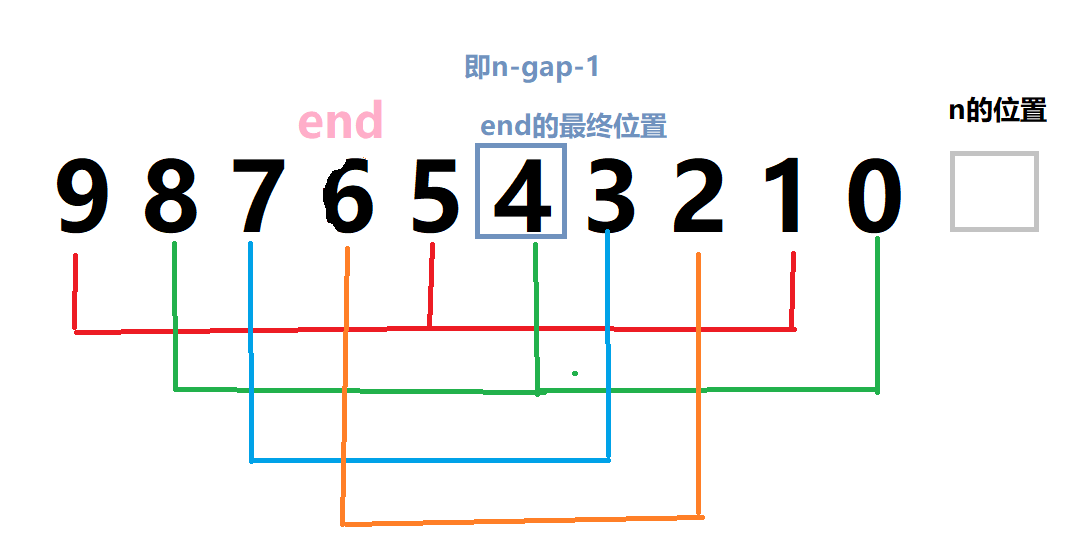
完结撒花~