本文是《机器学习入门基础》（黄海广著）的第十章的部分内容。

XGBoost算法

XGBoost是2014年2月由华盛顿大学的博士生陈天奇发明的基于梯度提升算法(GBDT)的机器学习算法，其算法不但具有优良的学习效果，而且训练速度高效，在数据竞赛中大放异彩。

XGBoost 是大规模并行Boosting Tree 的工具，它是性能和速度俱佳的开源Boosting Tree 工具包，比常见的工具包快很多倍。XGBoost 和 GBDT 两者都是Boosting 方法，除了工程实现、解决问题上的一些差异外，最大的不同就是目标函数的定义。

10.5.1 算法思想

XGBoost算法原理主要是以下几个方面：

1.防止过拟合

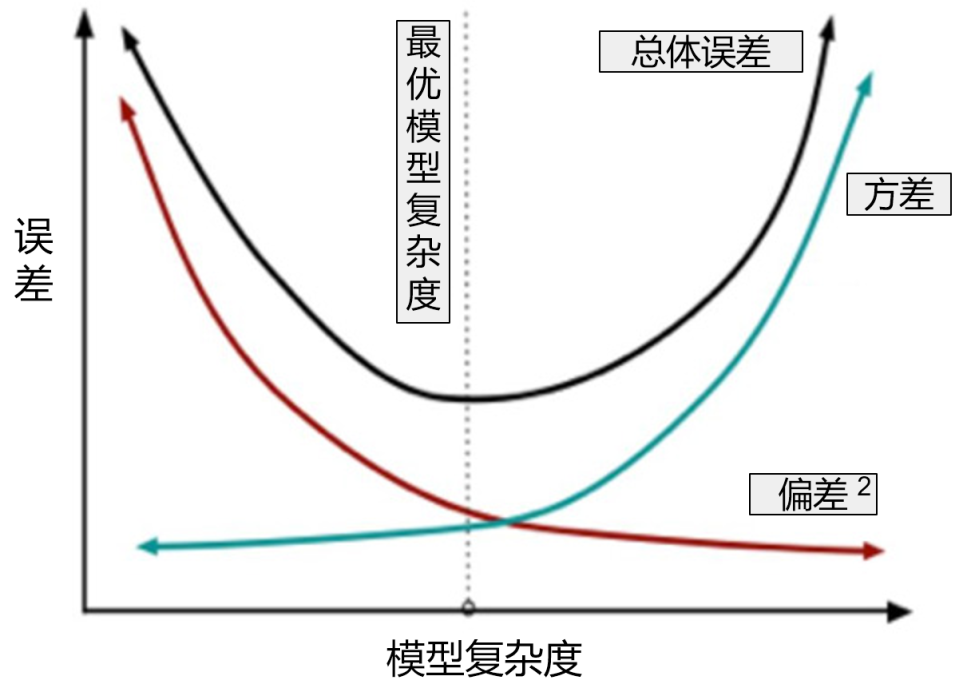
机器学习算法的泛化误差可以分为偏差(Bias)和方差(Variance)两部分。偏差指的是算法的期望预测与真实预测之间的偏差程度，反应了模型本身的拟合能力；方差度量了同等大小的训练集的变动导致学习性能的变化，刻画了数据扰动所导致的影响。

如图10-9所示，随着机器学习的模型复杂度增加，偏差越来越小，但方差却越来越大，而当模型越简单时，模型的方差很小，偏差却往往越大，也就是说，高方差导致过拟合，而高偏差导致欠拟合。

图10-9 机器学习方差和偏差

XGBoost有效解决了过拟合问题，对叶节点的权重进行了惩罚，防止过拟合，惩罚相当于添加了正则项，即目标函数为：训练损失加上正则项。

2.采用二阶泰勒展开加快收敛

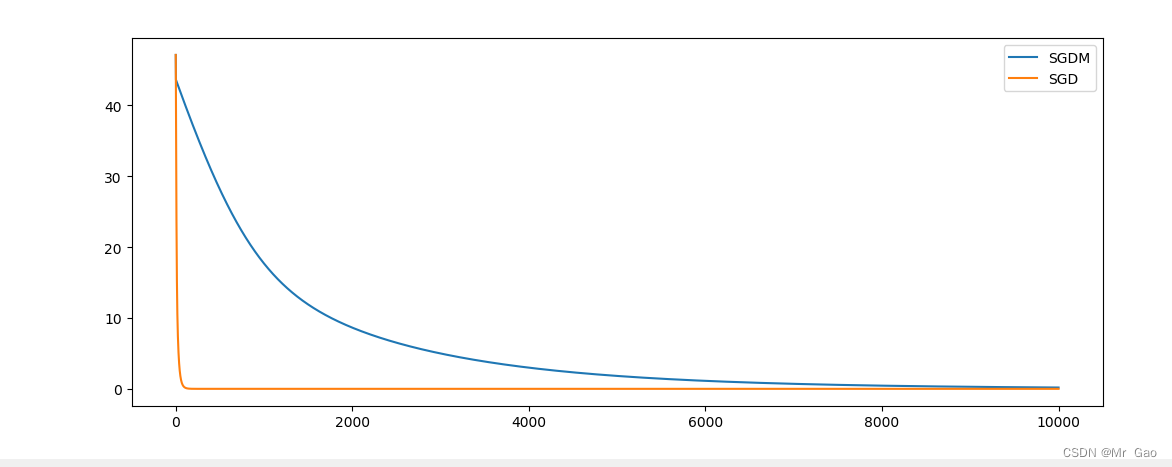
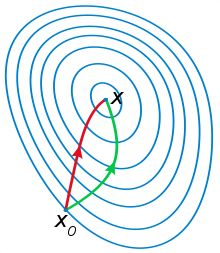
GBDT的损失函数用了一阶收敛，用到了梯度下降，XGBoost的方法是用牛顿法进行二阶收敛，即将损失函数做二阶泰勒展开，使用前两阶作为改进的残差。梯度下降法是用了目标函数的一阶偏导数，而牛顿法就是用用了目标函数的二阶偏导数，二阶偏导数考虑了梯度的变化趋势，所以牛顿法会更容易收敛。图10-10显示了牛顿法(左)和梯度下降法(右)的迭代路径，可以发现，左边的路径更符合最优下降路径。使用二阶收敛，这也是XGBoost加快收敛的原因。

图10-10 牛顿法(左)和梯度下降法(右)

3.树构造的分裂条件采用导数统计量

在寻找最佳分割点时，XGBoost 也实现了一种完全搜索式的精确的贪心算法(Exact Greedy Algorithm)。这种搜索算法会遍历一个特征上所有可能的分裂点，分别计算其损失减小量，然后选择最优的分裂点。根据结构分数的增益情况计算出来选择哪个特征的哪个分割点，某个特征的重要性，就是它在所有树中出现的次数之和。即增益(Gain)计算完了之后会选择一个增益最高的特征来分裂，然后这个特征的重要性加1。

4.支持并行计算，可以采用多线程优化技术

XGBoost的并行，并不是说每棵树可以并行训练，XGBoost本质上仍然采用boosting思想，每棵树训练前需要等前面的树训练完成才能开始训练。

XGBoost的并行，指的是特征维度的并行：在训练之前，每个特征按特征值对样本进行预排序，并存储为Block结构，在后面查找特征分割点时可以重复使用，而且特征已经被存储为一个个block结构，那么在寻找每个特征的最佳分割点时，可以利用多线程对每个block并行计算。

10.5.2 XGBoost算法推导

XGBoost中最主要的基学习器为CART(分类与回归树)，这里定义是叶子的权重， 是将每个节点分配给叶子的函数，是树的数量，并定义为一个常数。假设前步迭代优化得到的模型为，在第步中，待求参数为，则第步的目标函数为：

公式(10.14)第一部分是预测值和目标真实值之间的训练误差，第二部分是每棵树的复杂度之和。

根据泰勒展开公式，使用了二阶泰勒展开：

把看成则，就可以看成，则：

公式(10.16)中：

为的一阶偏导数：

为的二阶偏导数：

则公式(10.14)可以转化为：

在这里，我们首先改进一棵树的定义 如下：

在 XGBoost 中，我们将复杂度定义为：

γ

则目标函数可以定义为：

很明显，是一个常数，可以用替代，对于目标函数无影响，则目标函数可以转换为：

γ

其中定义是分配给第  个叶子的数据点的索引的集合。因为在同一叶子上，所有数据点的分数相同，所以在第二行中，我们更改了总和的索引。因此公式(10.23)等价于：

γγ

即：

γ

我们可以通过定义，来进一步压缩表达式，则：

γ

对求偏导，如果有一个给定的树的结构，那么在上式达到最小的情况下(即导数为0)，得到：

则：

γ

并且得到相对应的最优目标函数值：

以图10-11为例：

图10-11 决策树案例

根据已知的数据，得到相应的参数如图10-12：

图10-12 决策树参数

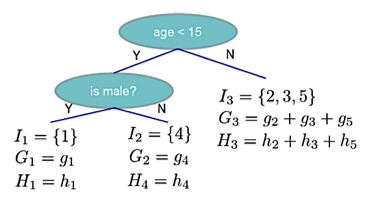
图10-12的数据，，根据公式(10.30)，则：

$分数越小，代表这个树的结构越好。

在寻找最佳分割点时，使用一种完全搜索式的精确贪心算法(Exact Greedy Algorithm)。这种搜索算法会遍历一个特征上所有可能的分裂点，分别计算其损失减小量，然后选择最优的分裂点。精确贪心算法的流程见算法10.1。

算法10.1精确贪心算法

算法思路：

由于树的结构是未知的，而且也不可能去遍历所有的树结构。因此，XGBoost采用贪婪算法来分裂节点，从根节点开始，遍历所有属性，遍历属性的可能取值，计算复杂度是：决策树叶子节点数减去1。根据定义，记分到左、右子树的样本集为、，，则分裂该节点导致的损失减少值为：

即：

其中：为分割后左子树的分数，为分割后右子树的分数，为未分割的树的分数，为新叶子的正则化项，即加入新叶子节点引入的复杂度代价，我们希望找到一个属性以及其对应的大小，使得取值最大。

10.5.3 XGBoost算法总结

XGBoost是算法竞赛中最热门的算法之一，它将GBDT的优化走向了一个极致：

(1) XGBoost生成CART树考虑了树的复杂度，GDBT未考虑，GDBT在树的剪枝步骤中考虑了树的复杂度。

(2) XGBoost是拟合上一轮损失函数的二阶导展开，GDBT是拟合上一轮损失函数的一阶导展开，因此，XGBoost的准确性更高，且满足相同的训练效果，需要的迭代次数更少。

(3) XGBoost与GDBT都是逐次迭代来提高模型性能，但是XGBoost在选取最佳分割点时可以开启多线程进行，大大提高了运行速度。当然，后续微软又出了LightGBM，在内存占用和运行速度上又做了不少优化，但是从算法本身来说，优化点则并没有比XGBoost多。

原文出自这本书：