文章目录
- 说明
- BP神经网络
- 1.基础知识
- 3 代码理解
- 3.1 数据的初始化
- 3.2 训练过程 train方法
- 3.3 forward 前向传播函数
- 3.4 backPropagation反向传播函数
说明
闵老师的文章链接: 日撸 Java 三百行(总述)_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护:https://github.com/fulisha-ok/sampledata
BP神经网络
1.基础知识
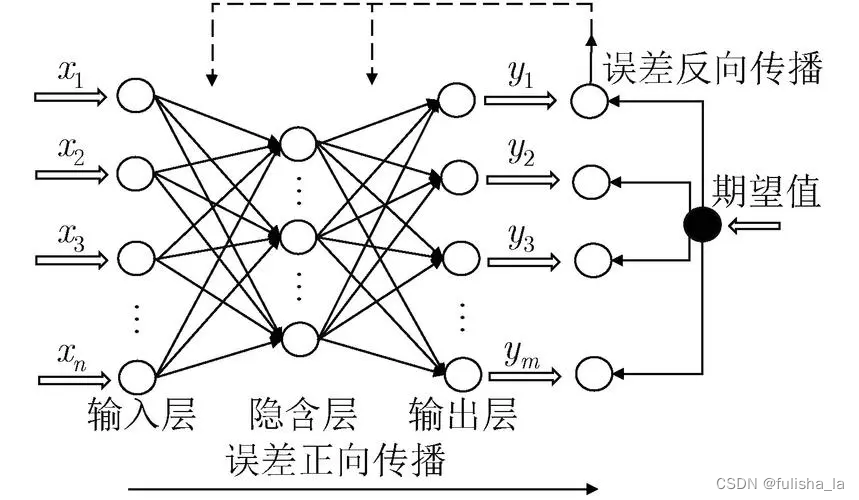
BP神经网络由多个神经元按层次排列而成,通常分为输入层、隐藏层和输出层,其中隐藏层可以为多层,结构如下所示。BP神经网络通过前向传播和反向传播两个过程来进行训练。
- 前向传播
将输入数据从输入层经过各层的神经元传递至输出层的过程,每个神经元将输入值与权重相乘并求加权和,经过激活函数处理后输出给下一层的神经元。这样一层层传递,直到输出层得到最终的预测结果。前向传播的过程相对来说比较简单。 - 反向传播
根据预测结果与真实标签之间的差异,通过调整网络中的权重来减小预测误差的过程。反向传播利用梯度下降优化算法,从输出层开始,根据误差计算每个神经元的梯度,并将梯度信息传递回前一层,以调整权重。反向传播的推导过程我认为是有点难度的,具体的推导过程可以参考文章和这篇
3 代码理解
3.1 数据的初始化
因为在代码中几个成员变量的声明需要理解,不然对代码的理解会有些困难,因此我通过图形来画出对这些变量的一个初始赋值情况:
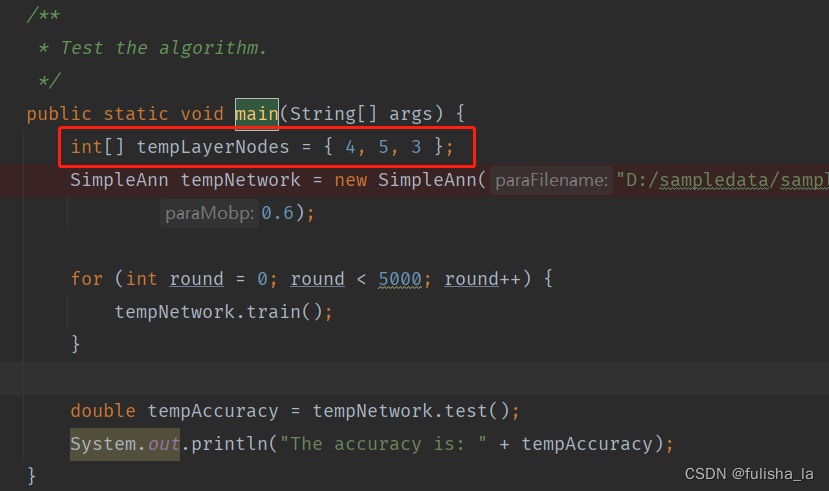
假设我tempLayerNodes的值为{ 4, 5, 3 },代表的意思就是一共有3层,其中输入层有4个结点,隐藏层有5个结点,输出层有3个结点。我们通过SimpleAnn构造函数,数据会初始化为什么样呢?如下图所示:
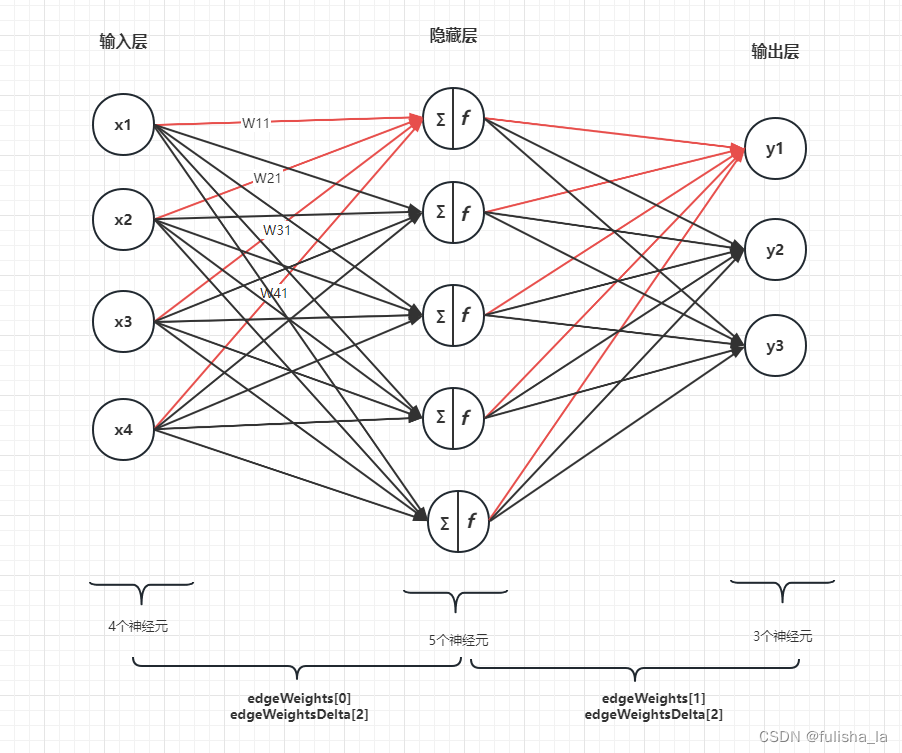
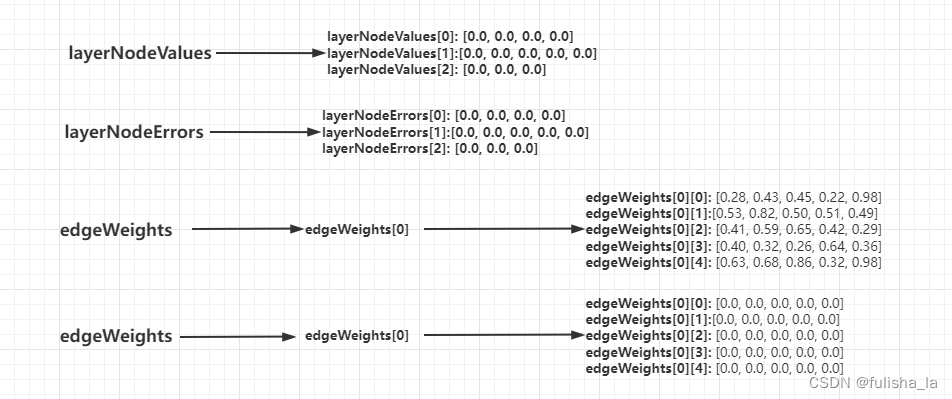
经过初始化:
- layerNodeValues:layerNodeValues[i],其中i代表第i层,layerNodeValues[i][j]代表每i层第j结点在前向传播过程具体的值:值应该是加权和+激活函数最后得出的值
- layerNodeErrors:layerNodeErrors[i],其中i代表第i层,layerNodeErrors[i][j]代表在反向传播过程中每i层第j结点的误差值
- edgeWeights 这是一个三维数组,存储了边的权重值。edgeWeights[i]表示第i层,edgeWeights[i][j][k]表示从第i层的第j个节点到第i+1层的第k个结点
- edgeWeightsDelta 与edgeWeights的维度相同,记录在反向传播过程中,每条边权重需要更新的量
注:edgeWeights ,edgeWeightsDelta 在初始化时公式如下,表明我们是加入了偏置项,如下图的edgeWeights[0][4]: [0.63, 0.68, 0.86, 0.32, 0.98]就是边的偏置项
edgeWeights[l] = new double[layerNumNodes[l] + 1][layerNumNodes[l + 1]];
edgeWeightsDelta[l] = new double[layerNumNodes[l] + 1][layerNumNodes[l + 1]];
3.2 训练过程 train方法
这一个for循环是对我们读入的数据样本进行训练,tempInput就是我们没一次样本的输入数据,tempTarget是预期的实际值。forward是前向传播函数和backPropagation是反向传播函数
/**
* Train using the dataset.
*/
public void train() {
double[] tempInput = new double[dataset.numAttributes() - 1];
double[] tempTarget = new double[dataset.numClasses()];
for (int i = 0; i < dataset.numInstances(); i++) {
// Fill the data.
for (int j = 0; j < tempInput.length; j++) {
tempInput[j] = dataset.instance(i).value(j);
}
// Fill the class label.
Arrays.fill(tempTarget, 0);
tempTarget[(int) dataset.instance(i).classValue()] = 1;
// Train with this instance.
forward(tempInput);
backPropagation(tempTarget);
}
}
3.3 forward 前向传播函数
将输入数据经过网络各层处理,最后一层输出结点的值
public double[] forward(double[] paraInput) {
// Initialize the input layer.
for (int i = 0; i < layerNodeValues[0].length; i++) {
layerNodeValues[0][i] = paraInput[i];
}
// Calculate the node values of each layer.
double z;
for (int l = 1; l < numLayers; l++) {
for (int j = 0; j < layerNodeValues[l].length; j++) {
// Initialize according to the offset, which is always +1 -偏置项(offset)
z = edgeWeights[l - 1][layerNodeValues[l - 1].length][j];
// Weighted sum on all edges for this node.
for (int i = 0; i < layerNodeValues[l - 1].length; i++) {
z += edgeWeights[l - 1][i][j] * layerNodeValues[l - 1][i];
}
// Sigmoid activation.
// This line should be changed for other activation functions.
layerNodeValues[l][j] = 1 / (1 + Math.exp(-z));
}
}
return layerNodeValues[numLayers - 1];
}
假设我们读入的样本是
- layerNodeValues[0][i] 初始化我们的输入数据
- 函数中的三层循环
最外层循环中,int l = 1; l < numLayers; l++表示我们从第二层开始到最后一层
内两层循环中:计算当前层的每个结点的加权和并通过激活函数更新值。具体计算方式:- z = edgeWeights[l - 1][layerNodeValues[l - 1].length][j]; 获取边的偏置项数据
- 计算加权和 最内层循环:z += edgeWeights[l - 1][i][j] * layerNodeValues[l - 1][i];
- 激活函数:sigmoid函数
σ ( x ) = 1 1 + e − x \sigma (x) = \frac{1}{ 1 +e^{-x}} σ(x)=1+e−x1
例如图示计算 第一层第0个结点的值,即layerNodeValues[1][0]的值:
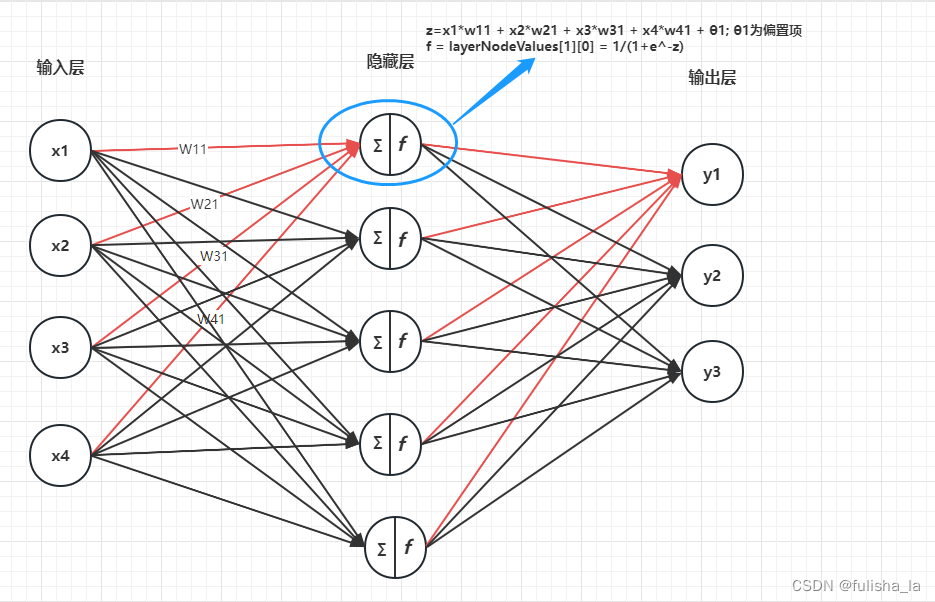
3.4 backPropagation反向传播函数
虽然代码行数挺少,但感觉这个过程的公式推导挺难,需要去百度自行消化。可以参考这个公式(公式推导具体过程参考文章)
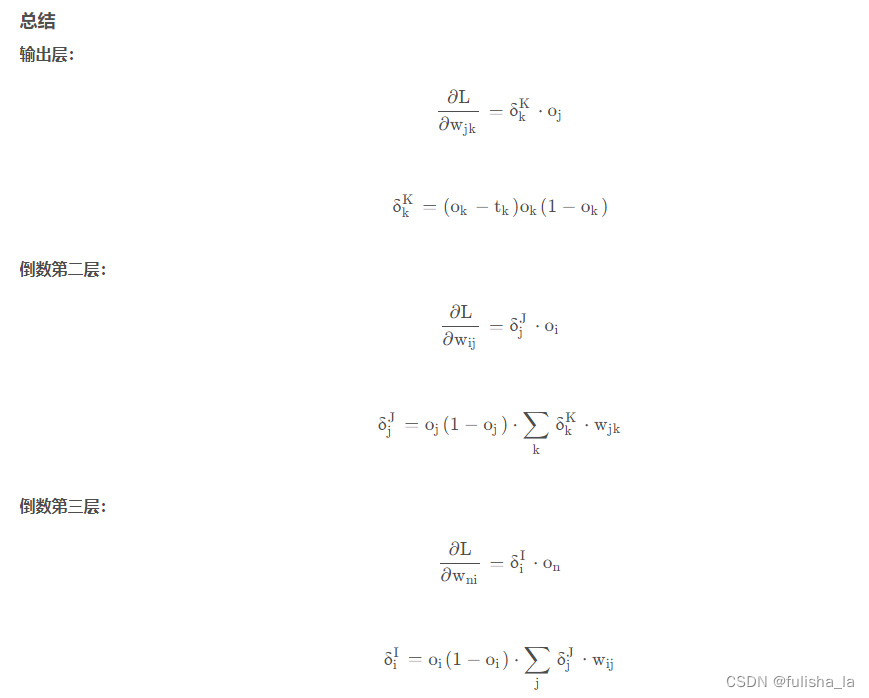
其中
δ
k
K
\delta _{k}^{K}
δkK是我们的误差项,
∂
L
∂
w
j
k
\frac{\partial L}{\partial w_{jk}}
∂wjk∂L表示损失函数(L)关于权重
w
j
k
w_{jk}
wjk的偏导数(也可以理解为梯度)。
我们结合上面的公式可以知道,我们在反向传播函数中更新权重是结合梯度下降来进行优化参数的。
public void backPropagation(double[] paraTarget) {
// Step 1. Initialize the output layer error.
int l = numLayers - 1;
for (int j = 0; j < layerNodeErrors[l].length; j++) {
layerNodeErrors[l][j] = layerNodeValues[l][j] * (1 - layerNodeValues[l][j])
* (paraTarget[j] - layerNodeValues[l][j]);
}
// Step 2. Back-propagation even for l == 0
while (l > 0) {
l--;
// Layer l, for each node.
for (int j = 0; j < layerNumNodes[l]; j++) {
double z = 0.0;
// For each node of the next layer.
for (int i = 0; i < layerNumNodes[l + 1]; i++) {
if (l > 0) {
z += layerNodeErrors[l + 1][i] * edgeWeights[l][j][i];
}
// Weight adjusting.
edgeWeightsDelta[l][j][i] = mobp * edgeWeightsDelta[l][j][i]
+ learningRate * layerNodeErrors[l + 1][i] * layerNodeValues[l][j];
edgeWeights[l][j][i] += edgeWeightsDelta[l][j][i];
if (j == layerNumNodes[l] - 1) {
// Weight adjusting for the offset part.
edgeWeightsDelta[l][j + 1][i] = mobp * edgeWeightsDelta[l][j + 1][i]
+ learningRate * layerNodeErrors[l + 1][i];
edgeWeights[l][j + 1][i] += edgeWeightsDelta[l][j + 1][i];
}
}
// Record the error according to the differential of Sigmoid.
// This line should be changed for other activation functions.
layerNodeErrors[l][j] = layerNodeValues[l][j] * (1 - layerNodeValues[l][j]) * z;
}
}
}
-
第一个for循环计算输出结点的误差值。
误差值: δ k K = ( o k − t k ) ∗ o k ∗ ( 1 − o k ) δ_k^K = (o_k - t_k) * o_k * (1 - o_k) δkK=(ok−tk)∗ok∗(1−ok),其中 o k {o_k } ok为激活函数输出的值- layerNodeValues[l][j]在当前的权重下的输出结果
- (paraTarget[j] - layerNodeValues[l][j]):真是值和预测值之间的差异
- layerNodeValues[l][j] 和补数 (1 - layerNodeValues[l][j]) 的乘积,即为激活函数(Sigmoid 函数)的导数
-
while循环 更新权重
edgeWeightsDelta:调整第 l 层的第 j 个节点与第 l+1 层的第 i 个节点之间的连接上的权重增量,利用梯度下降算法来调整(结合了参数mobp和learningRate 系数):(mobp动力系数,加速收敛;learningRate学习率控制权重调整的幅度),而在代码中有一个if判断j == layerNumNodes[l] - 1是考虑偏置结点。
layerNodeErrors[l + 1][i]是我们已经知道的他下一层的误差值(输出层和隐藏层的误差值计算不一样哦~)
edgeWeightsDelta[l][j][i] = mobp * edgeWeightsDelta[l][j][i] + learningRate * layerNodeErrors[l + 1][i] * layerNodeValues[l][j];
edgeWeights[l][j][i] += edgeWeightsDelta[l][j][i];
更新当前层的结点误差(主要还是隐藏层)。
layerNodeErrors[l][j] = layerNodeValues[l][j] * (1 - layerNodeValues[l][j]) * z;
运行结果: