一、案例介绍

某医院用三种穴位针刺治疗急性腰扭伤，现在想比较三种穴位针刺效果有无差别，结果汇总如下表：

二、问题分析

本案例想比较三种穴位针刺效果有无差别，可以使用RxC卡方检验进行分析。

通常情况下，共有三种卡方值，分别是Pearson卡方、yates校正卡方、Fisher卡方，具体分析时需要使用哪一种卡方值，需要结合样本量、期望频数大小、X和Y的类别个数等进行判断。使用SPSSAU卡方检验进行分析时，SPSSAU将自动进行选择，具体选择标准在后续分析中会进行详细说明。

使用RxC卡方检验进行分析时，需要满足以下两个条件：

条件1：分组变量和观察变量均为分类变量；本案例穴位和治愈情况均为分类变量满足条件1。

条件2：观测值之间相互独立；本案例中200名患者均相互独立，治疗过程不存在互相干扰的情况，满足条件2。

所以，可以使用RxC卡方检验进行分析。

三、软件操作及结果解读

（一）上传数据

首先将数据整理成RxC卡方检验正确的格式，穴位和针刺效果的关系研究，穴位分为3类，针刺效果分为2类，因而共有3*2=6种组合情况，每类组合情况的样本数量单独一列作为权重值进行标识，最终将本案例数据整理成如下格式：

将整理好的数据上传至SPSSAU系统，点击右上角上传数据按钮，按提示上传数据，操作如下：

上传数据完成后，接下来开始进行RxC卡方检验分析。

（二）软件操作

在SPSSAU医学/实验研究模块，选择【卡方检验】，将“穴位”拖拽到右侧X(定类)分析框中，将“治疗情况”拖拽到右侧Y(定类)分析框中，将“权重”拖拽到右侧“加权项”分析框中，然后点击“开始分析”，操作如下图：

（三）结果解读

1、卡方检验分析结果

SPSSAU输出卡方检验分析结果如下：

从上表可以看出，卡方值为32.7523，对应p值=0.000<0.05，按α=0.05的水平，拒绝原假设，接受备择假设，即可以认为三种穴位针刺效果的差异有统计学意义。进而可以通过对比选择百分比（括号内值）进行比较，例如后溪穴中，未愈人数占比18.367%，治愈人数占比81.633%。可以通过SPSSAU自动输出的穴位和治疗情况交叉图进行直观对比，如下图：

同学们可能发现了，虽然输出了卡方值，但是具体为Pearson卡方、连续校正Yates卡方还是Fisher卡方，我们现在还不得而知，需要通过下方的卡方检验统计量过程值进行判断（这一选择过程已经被SPSSAU自动化处理，非专业用户可以忽略）。

2、卡方检验统计量过程值

卡方检验统计量过程值就是用于判断，卡方检验最终应该使用Pearson卡方、连续校正Yates卡方还是Fisher卡方。

3类卡方具体选择标准如下：

下述中n代表总样本量；E代表期望频数；R代表X的类别个数；C代表Y的类别个数。

• 针对2*2（R=2，C=2）
  n>=40 且 E全部>=5则使用Pearson卡方；
  n>=40但其中有1个格子出现1 <=E<5则使用yates校正卡方；
  任何一格子出现E <1或n<40则使用Fisher卡方;
• 针对R*C(R，C中任意一个大于2；且R>=2,且C>=2)

E全部>1 且 1 <=E<5格子的比例小于20% 则使用Pearson卡方，否则使用yates校正卡方。

本案例为R*C类型，R=3>2，E≥5的格子个数为6，占比为100%（共6个格子），所以应该使用yates校正卡方。

特别提示：Pearson卡方和yates校正卡方完全相同是正常现象，多数情况下二者完全相等。

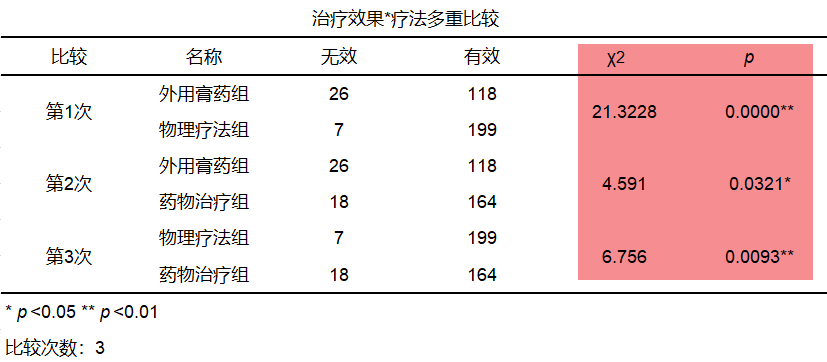
3、深入分析——多重比较

RxC卡方检验的结果只能判断各组之间是否存在差异，但是不能知道具体哪两组之间存在差异，SPSSAU会同时输出多重比较的结果，用于进行两两比较，结果如下表：

从上表可以看出，第1次对比人中穴和后溪穴针刺效果是否有差异，卡方值为14.2447，对应p值为0.0002<0.0167，说明人中穴和后溪穴两种针刺效果的差异有统计学意义。同理可知，人中穴与腰痛穴两种针刺效果的差异无统计学意义（卡方值为1.2635，p=0.2610>0.0167）；后溪穴与腰痛穴针刺效果的差异有统计学意义（卡方值为30.7536，p=0.0000<0.0167）。

特别提示：多重比较时，检验次数增多会增加一类错误的概率，建议使用校正显著性水平(Bonferroni校正)；如本案例中显著性水平为0.05，两两比较次数为3次，那么Bonferroni校正显著性水平为0.05/3次=0.0167，即p值需要与0.0167进行对比，而不是0.05。

四、结论

本案例通过使用RxC卡方检验，具体为yates校正卡方，比较3种穴位针刺效果的差异性，研究发现，3种穴位针刺效果的差异具有统计学意义。经事后比较进行两两穴位之间对比发现，人中穴与后溪穴、后溪穴与腰痛穴两两之间的针刺效果差异有统计学意义，而人中穴和腰痛穴之间的针刺效果的差异无统计学意义。

五、知识小贴士

（1）卡方检验多重比较是什么意思？

SPSSAU默认提供多重比较功能，且SPSSAU仅针对第1个Y进行，可通过更换Y的位置实现其它分析项的多重比较，X或Y的选项个数大于10时不进行多重比较。多重比较时，SPSSAU默认提供Pearson卡方检验值。

（2）多重比较什么是校正显著性水平？

多重比较时，SPSSAU默认提供Pearson卡方检验值，多重比较时，检验次数增多会增加一类错误的概率，建议使用校正显著性水平(Bonferroni校正)，比如如果显著性水平为0.05，并且两两比较次数为3次，那么Bonferroni校正显著性水平为0.05/3次=0.0167，即p值需要与0.0167进行对比，而不是0.05。

参考文献：

[1]颜红,徐勇勇.医学统计学.第3版[M].人民卫生出版社,2015