卡方检验之多重比较

news2024/11/25 10:33:06

一、案例介绍

某医师研究物理疗法、药物治疗和外用膏药3种疗法治疗周围性面神经麻痹的疗效，通过整体卡方检验已经得知3种疗法有效率的差异有统计学意义（χ2=21.0377，p=0.000）的结论。现在想进一步知道，具体是哪两种疗法之间的差异有统计学意义。数据如下图1：

图1

二、问题分析

本案例已经知道3种疗法有效率(%)的差异具有统计学意义，接下来想知道具体是哪两种疗法之间有差异，可以使用卡方检验的多重比较进行两两类别组合重复进行卡方检验。在SPSSAU中，直接使用RxC卡方检验进行分析会自动输出多重比较结果。

三、软件操作及结果解读

（一）上传数据

首先将数据整理成RxC卡方检验正确的格式，疗法和治疗效果的关系研究，疗法分为3类，治疗效果分为2类，因而共有3*2=6种组合情况，每类组合情况的样本数量单独一列作为权重值进行标识，最终将本案例数据整理成如下图2格式：

图2

将整理好的数据上传至SPSSAU系统，点击右上角上传数据按钮，按提示上传数据，操作如下图3：

图3

上传数据完成后，接下来开始进行卡方检验多重比较分析。

（二）软件操作

在SPSSAU医学/实验研究模块，选择【卡方检验】，将“疗法”拖拽到右侧X(定类)分析框中，将“治疗效果”拖拽到右侧Y(定类)分析框中，将“人数”拖拽到右侧“加权项”分析框中，然后点击“开始分析”，操作如下图4：

图4

（三）结果解读

1、卡方检验分析结果

SPSSAU首先输出整体卡方检验分析结果如下图5：

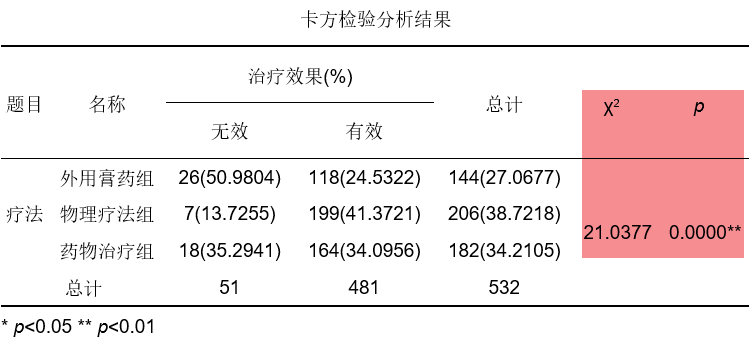
图5

得到已知结论，3种疗法的治疗效果差异具有统计学意义（χ2=21.0377，p=0.000），接下来进行多重比较，进行两两疗法之间的对比。

2、治疗效果*疗法多重比较

SPSSAU输出卡方检验的多重比较结果如下图6：

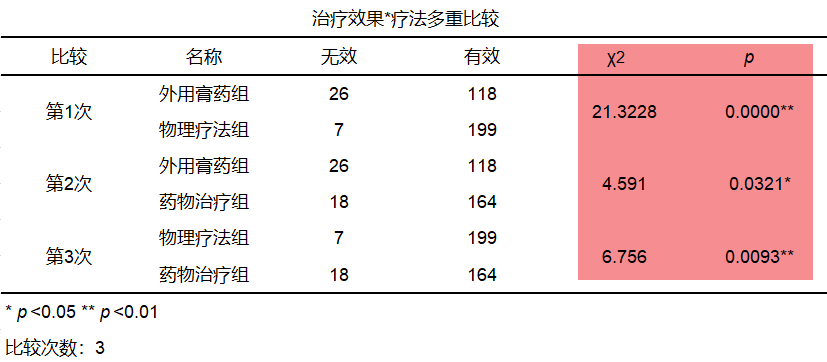
图6

从上表可以得知，3种疗法两两之间进行多重比较：第1次对比外用膏药和物理疗法的治疗效果是否有差异，卡方值为21.3228，对应p值为0.000<0.0167，说明外用膏药和物理疗法两种疗法的治疗效果的差异有统计学意义。同理可知，外用膏药和药物治疗两种疗法的治疗效果的差异无统计学意义（卡方值为4.591，p=0.0321>0.0167）；物理疗法和药物治疗两种疗法的治疗效果差异有统计学意义（卡方值为6.756，p=0.0093<0.0167）。

特别提示：多重比较时，检验次数增多会增加一类错误的概率，建议使用校正显著性水平(Bonferroni校正)；如本案例中显著性水平为0.05，两两比较次数为3次，那么Bonferroni校正显著性水平为0.05/3次=0.0167，即p值需要与0.0167进行对比，而不是0.05。

四、结论

本案例使用卡方检验多重比较进行3种疗法两两之间治疗效果差异性比较，结果显示，按校正显著性水平0.0167水准，外用膏药和物理疗法、物理疗法和药物治疗这两组之间的治疗效果的差异性具有统计学意义；而外用膏药和药物治疗的治疗效果的差异无统计学意义。结合图1有效率分析，可以认为物理疗法的有效率高于其他两种疗法，但是还不能认为外用药膏和药物治疗的有效率有差异。