文章目录
- 1.神经网络
- 2.反向传播算法
- 3.激活函数
- 4.损失函数
- 5.神经网络的使用场景
- 参考
1.神经网络
神经网络是一种计算模型,它受到人脑神经元之间连接和信息处理方式的启发。它由许多简单的处理单元(称为神经元或节点)组成,并通过这些节点之间的连接进行信息传递和处理。
神经网络广泛应用于许多领域,包括图像和语音识别、自然语言处理、机器翻译、推荐系统等。它能够通过学习大量数据来进行模式识别和特征提取,从而实现复杂的任务和问题求解。
本文以多层感知机(Multi-Layer Perceptron,MLP)这一神经网络为例来进行介绍。
- 结构:
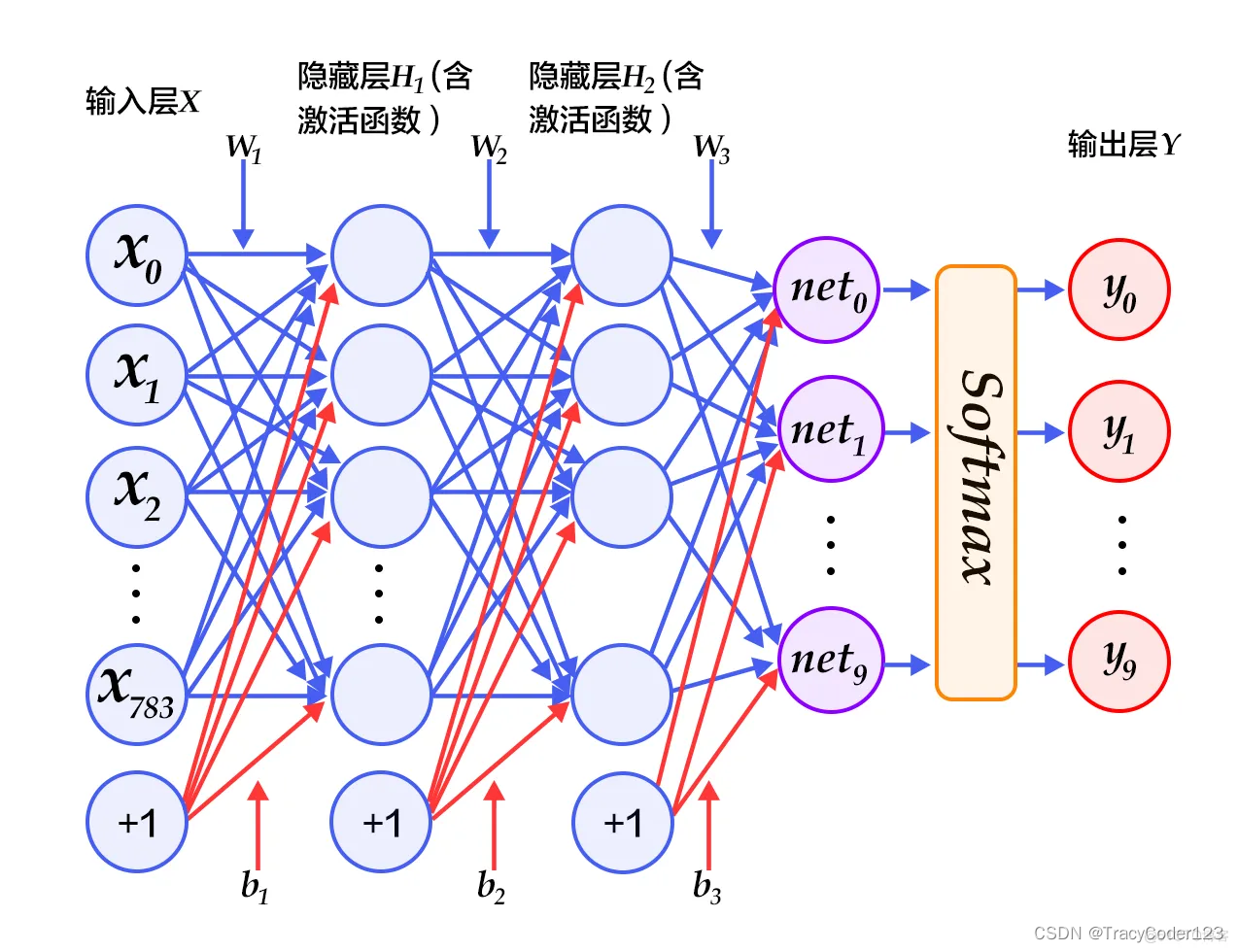
一个神经网络通常由多个层组成,包括输入层、隐藏层和输出层。每个节点接收来自上一层节点的输入,并通过激活函数对输入进行处理,然后将输出传递给下一层节点。隐藏层在输入层和输出层之间起到了“过渡”或“提取特征”的作用。
h
1
(
x
)
=
f
(
W
1
x
+
b
1
)
h_1(x) = f(W_1x+b_1)
h1(x)=f(W1x+b1)
h
l
(
x
)
=
f
(
W
l
h
l
−
1
(
x
)
+
b
l
)
h_l(x) = f(W_lh_{l-1}(x)+b_l)
hl(x)=f(Wlhl−1(x)+bl)
y
(
x
)
=
f
(
W
L
h
L
−
1
(
x
)
+
b
L
)
y(x) = f(W_{L}h_{L-1}(x)+b_{L})
y(x)=f(WLhL−1(x)+bL)
其中,
f
f
f为激活函数,
W
L
W_{L}
WL为输出层权重矩阵,
b
L
b_{L}
bL为输出层偏置。
- 训练:
神经网络的学习发生在训练阶段,利用训练数据不断调整节点之间的连接权重和阈值值,以最小化预测输出与实际输出之间的误差。常用的训练算法包括 反向传播算法和梯度下降。
2.反向传播算法
反向传播算法(Backpropagation Algorithm)是神经网络中常用的一种训练算法,用于调整神经网络的权重和偏差(即连接权重和阈值值),以使网络能够更好地逼近给定的训练数据。
反向传播算法的核心思想是通过计算预测输出与实际输出之间的误差,并将误差从输出层向输入层逐层反向传播,以更新网络中的权重和偏差。
具体来说,反向传播算法分为两个主要的步骤:前向传播和反向传播。
- 前向传播:从输入层开始,逐层计算每个节点的输出,直到达到输出层。在这个过程中,根据节点之间的连接权重和偏差,将输入信号通过激活函数进行处理,并传递到下一层节点,直到最终的输出。以下几个公式就是前向传播:
h
1
(
x
)
=
f
(
W
1
x
+
b
1
)
h_1(x) = f(W_1x+b_1)
h1(x)=f(W1x+b1)
h
l
(
x
)
=
f
(
W
l
h
l
−
1
(
x
)
+
b
l
)
h_l(x) = f(W_lh_{l-1}(x)+b_l)
hl(x)=f(Wlhl−1(x)+bl)
y
(
x
)
=
f
(
W
L
h
L
−
1
(
x
)
+
b
L
)
y(x) = f(W_{L}h_{L-1}(x)+b_{L})
y(x)=f(WLhL−1(x)+bL)
其中,
f
f
f为激活函数,
W
L
W_{L}
WL为输出层权重矩阵,
b
L
b_{L}
bL为输出层偏置。
- 反向传播:计算预测输出与实际输出之间的误差,并将误差从输出层向输入层逐层传播。根据误差值,按照链式法则(Chain Rule)计算每个节点的调整量。然后使用优化算法(如梯度下降),通过乘上学习率,更新神经网络中的连接权重和偏差。
在多层感知机中,反向传播用于更新模型参数,求解损失函数的梯度。设损失函数为 L L L,输出为 y y y,真实标签为 t t t,则反向传播的计算过程如下:
δ L = ∂ L ∂ y f ′ ( W L h L − 1 ( x ) + b L ) \delta_{L} = \frac{\partial L}{\partial y}f'(W_{L}h_{L-1}(x)+b_{L}) δL=∂y∂Lf′(WLhL−1(x)+bL)
δ l = ∂ L ∂ h l f ′ ( W l + 1 T δ l + 1 ) \delta_{l} = \frac{\partial L}{\partial h_{l}}f'(W_{l+1}^{T}\delta_{l+1}) δl=∂hl∂Lf′(Wl+1Tδl+1)
∂ L ∂ W l = h l − 1 δ l T \frac{\partial L}{\partial W_{l}} = h_{l-1}\delta_{l}^{T} ∂Wl∂L=hl−1δlT
∂ L ∂ b l = δ l \frac{\partial L}{\partial b_{l}} = \delta_{l} ∂bl∂L=δl
其中, δ L \delta_{L} δL为输出层误差, δ l \delta_{l} δl为第 l l l层隐藏层误差, f ′ f' f′为激活函数的导数。
反向传播算法反复迭代以上两个步骤,直到达到预定的停止条件(如误差收敛或达到最大训练次数)为止。通过训练过程中不断调整网络参数,神经网络能够逐渐优化并学习到与给定训练数据相匹配的模式和特征。
反向传播算法是神经网络中非常重要且常用的训练算法,它为神经网络的学习和调整提供了一种有效的方式。
3.激活函数
激活函数(Activation Function)是神经网络中的一种非线性函数,应用于神经元的输出,用于引入非线性变换和增加模型的表达能力。
在神经网络中,每个神经元都有一个激活函数,用于对输入信号进行处理,并将处理后的输出传递给下一层的神经元。激活函数的作用是将输入的加权和与偏差进行转换,以产生非线性的输出。
不同的激活函数具有不同的特性,如非线性、可导性和抑制/增强特定输入范围等。选择适当的激活函数对于神经网络的训练和学习非常重要,可以提高模型的表达能力和性能。
关于激活函数建议好好看下这篇博客
4.损失函数
损失函数(Loss Function)是用来衡量模型预测结果与真实值之间差异的函数。它是训练过程中最小化的目标函数,用来衡量模型在训练数据上的性能和误差大小。
在机器学习和深度学习中,常用的损失函数根据任务类型和目标不同,也有多种选择。以下是一些常见的损失函数:
-
均方误差(Mean Square Error, MSE):用于回归任务,计算预测值和真实值之间的平均平方差。MSE对异常值比较敏感。
-
交叉熵损失(Cross-Entropy Loss):用于分类任务,根据预测结果和真实标签之间的差距计算损失值。交叉熵损失比较适用于多分类任务。
-
对数损失(Log Loss):也用于二分类和多分类任务,衡量预测概率分布和真实标签之间的误差。
-
Hinge损失:用于支持向量机(Support Vector Machines, SVM)中,适合用于二分类。
-
KL散度(Kullback-Leibler Divergence):用于衡量两个概率分布之间的差异,常用于生成模型中。
选择合适的损失函数对于模型的训练和优化至关重要。通过最小化损失函数,模型可以通过反向传播算法(Backpropagation)调整参数以使预测结果逼近真实值,提高模型的性能和准确性。在多层感知机中,常用的损失函数为均方误差(MSE)和交叉熵(cross-entropy)。
5.神经网络的使用场景
多层感知机(Multi-Layer Perceptron, MLP)适用于许多任务,**特别是在分类和回归问题中表现良好。**以下是一些常见的任务,适合使用多层感知机:
-
分类任务:多层感知机可以用于解决二分类和多分类问题。通过在输出层使用适当的激活函数(如Sigmoid或Softmax),多层感知机可以对输入样本进行分类预测。
-
回归任务:多层感知机也可以用于解决回归问题,其中输出层不再使用激活函数,而是直接输出连续值。通过训练过程中的误差最小化,多层感知机可以对输入样本进行连续值的预测。
-
特征提取:多层感知机的隐藏层可以用来提取输入数据的特征表示。通过在多个隐藏层进行非线性变换,多层感知机可以从原始输入中逐层提取出更高级别的特征。
-
强化学习:多层感知机在强化学习任务中也常被用作值函数近似,用于根据当前状态预测最优动作的价值。
需要注意的是,在处理具有复杂结构和序列性质的数据(如文本、语音、图像)时,常常会将多层感知机与其他技术如卷积神经网络(CNN)和循环神经网络(RNN)结合使用,以更好地捕捉数据中的空间和时间相关性。
参考
https://blog.51cto.com/u_16099172/6290977
https://blog.csdn.net/weixin_39910711/article/details/114849349