【力扣】DP：1186. 删除一次得到子数组最大和

文章目录

【力扣】DP：1186. 删除一次得到子数组最大和
- 1. 题目描述
- 2. 题解
- - 2.1 不可行
  - 2.2 DP
- 参考

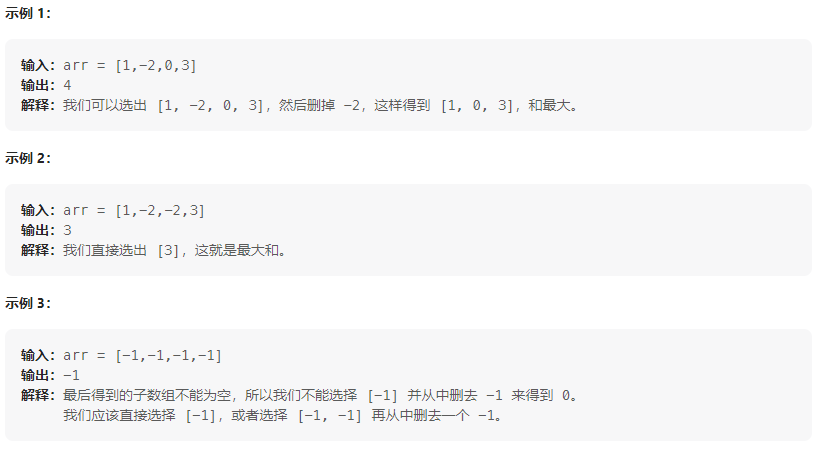
1. 题目描述

给你一个整数数组，返回它的某个非空子数组（连续元素）在执行一次可选的删除操作后，所能得到的最大元素总和。

换句话说，你可以从原数组中选出一个子数组，并可以决定要不要从中删除一个元素（只能删一次哦），（删除后）子数组中至少应当有一个元素，然后该子数组（剩下）的元素总和是所有子数组之中最大的。

注意，删除一个元素后，子数组不能为空。

2. 题解

2.1 不可行

暴力，列举所有组合。
前缀和，但是不知道删哪个

2.2 DP

可以将问题拆分成多个子问题，即求解以 arr[i] 结尾的最多删除一次的非空子数组的最大和。我们以 dp[i][k] 表示以 arr[i]结尾，删除 k 次的非空子数组的最大和（删除前的末尾元素为 arr[i]，就视为以 arr[i] 结尾）。初始时 dp[0][0]=arr[0]，dp[0][1]＝0（以 arr[0] 结尾，删除一次的非空子数组不存在，因此 dp[0][1]不会计入结果）。

当 i > 0 时，转移方程如下：

dp[i][0] = max⁡(dp[i−1][0], 0) + arr[i]
dp[i][1] = max⁡(dp[i−1][1] + arr[i], dp[i−1][0])

第一个转移方程表示：在不删除的情况下，以 arr[i] 为结尾的非空子数组的最大和 dp[i][0] 与 dp[i－1][0] 有关，当 dp[i−1][0]>0 时，直接将 arr[i] 与 i−1 时的最大非空子数组连接时，取得最大和，否则只选 arr[i] 时，取得最大和。
第二个转移方程表示：在删除一次的情况下，以 arr[i] 为结尾的非空子数组有两种情况：
- 不删除 arr[i]，那么选择 arr[i] 与 dp[i−1][1] 对应的子数组（已执行一次删除）。
- 删除 arr[i]，那么选择 dp[i−1][0] 对应的非空子数组（未执行一次删除，但是等同于删除了 arr[i]）。
- dp[i][1] 取以上两种情况的最大和的最大值。

注意到 dp[i][∗] 的值只与 dp[i−1][∗] 有关，因此我们可以只使用两个整数来节省空间。

class Solution {
public:
    int maximumSum(vector<int>& arr) {
        int dp0 = arr[0], dp1 = 0, res = arr[0];
        for (int i = 1; i < arr.size(); i++) {
            dp1 = max(dp0, dp1 + arr[i]);
            dp0 = max(dp0, 0) + arr[i];
            res = max(res, max(dp0, dp1));
        }
        return res;
    }
};