【LeetCode热题100】打卡第29天：二叉树的层序遍历&二叉树的最大深度

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

博客主页💖：知识汲取者的博客

LeetCode热题100专栏🚀：LeetCode热题100

Gitee地址📁：知识汲取者 (aghp) - Gitee.com

Github地址📁：Chinafrfq · GitHub

题目来源📢：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

二叉树的层序遍历

🔒题目

原题链接：104.二叉树的层序遍历

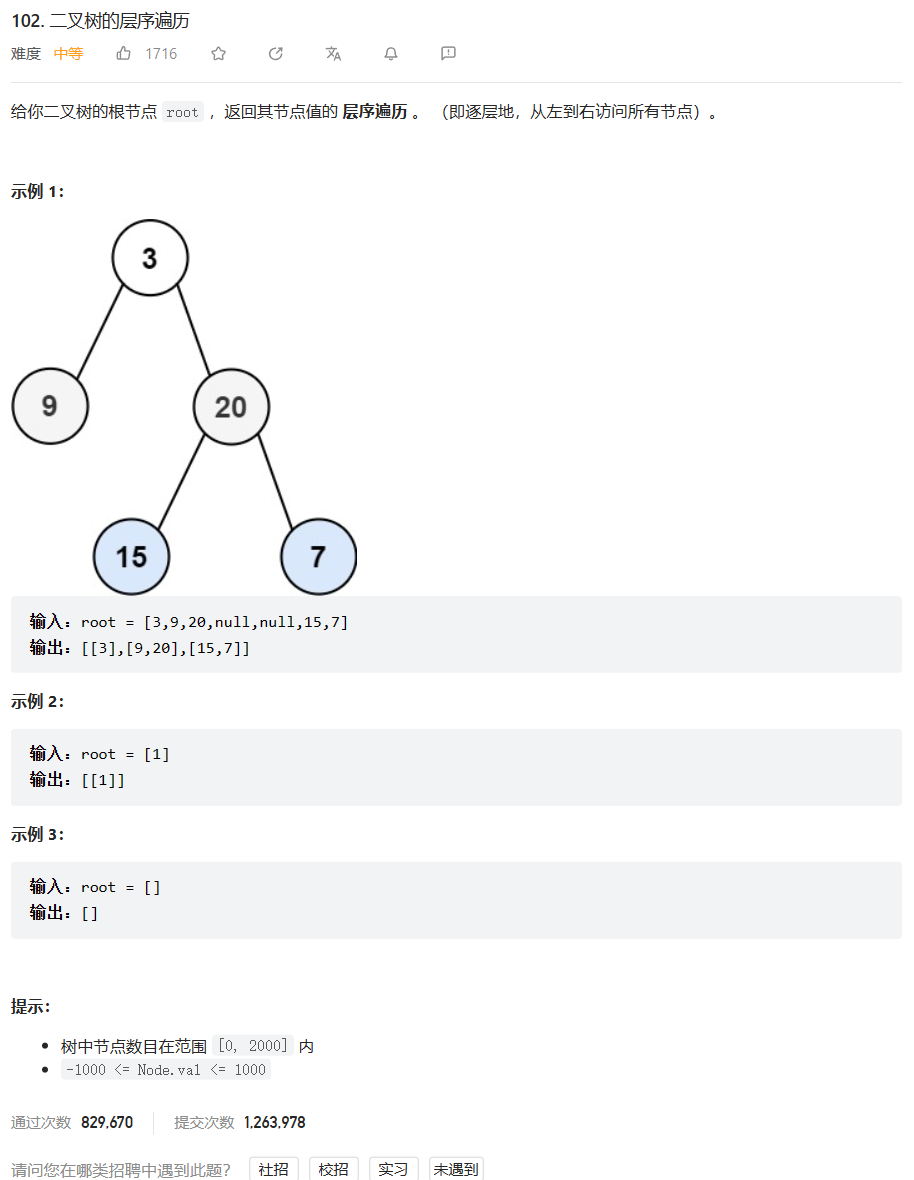
🔑题解

解法一：BFS

简单明了

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        if (root==null){
            // 防止后面出现NPE
            return Collections.emptyList();
        }
        List<List<Integer>> ans = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            // 用于存储当前层所有的叶子节点
            List<Integer> list = new ArrayList<>();
            // 遍历当前层的所有根节点，将当前层根节点下所有叶子节点存入队列中
            // 注意queue的长度是动态变化的，这里需要使用一个变量来存储初始长度
            int len = queue.size();　
            for (int i = 1; i <= len; i++) {
                TreeNode node = queue.poll();
                list.add(node.val);
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            ans.add(list);
        }
        return ans;
    }
}

复杂度分析：

时间复杂度： $O (n)$
空间复杂度： $O (n)$

其中 $n$ 为数组中元素的个数

二叉树的最大深度

🔒题目

原题链接：105.二叉树的最大深度

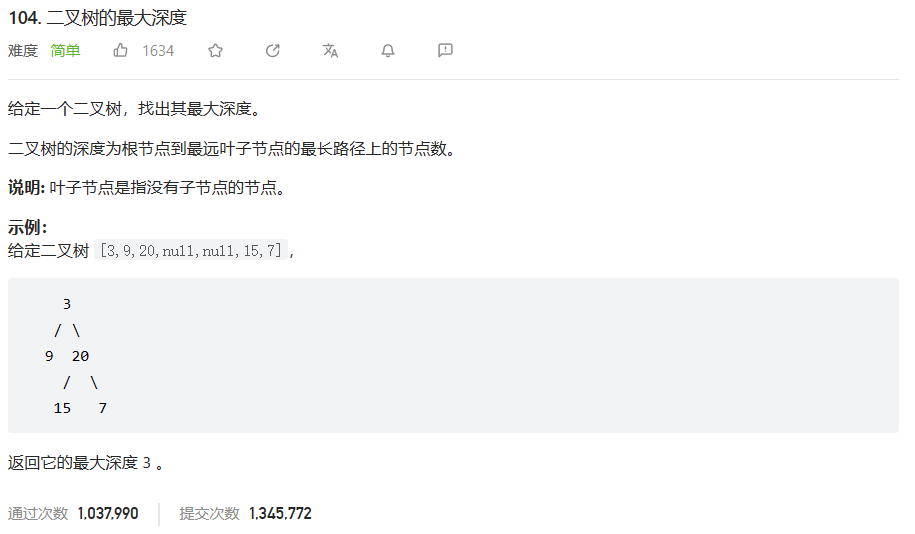
🔑题解

解法一：DFS

class Solution {
    private int max = Integer.MIN_VALUE;
    public int maxDepth(TreeNode root) {
        dfs(root, 0);
        return max;
    }

    private void dfs(TreeNode root, int count) {
        if (root==null){
            if (count > max){
                max = count;
            }
            return;
        }
        dfs(root.left, count+1);
        dfs(root.right, count+1);
    }
}

复杂度分析：

时间复杂度： $O (n)$
空间复杂度： $O (n)$

$n$ 为树中节点的数量

第二种写法：

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        } else {
            int left = maxDepth(root.left);
            int right = maxDepth(root.right);
            return Math.max(left, right) + 1;
        }
    }
}

解法二：BFS

这里是直接借鉴了二叉树的层序遍历

class Solution {
    public int maxDepth(TreeNode root) {
        if (root==null){
            return 0;
        }
        int count = 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()){
            count++;
            int len = queue.size();
            for (int i = 1; i <= len; i++) {
                TreeNode node = queue.poll();
                if (node.left!=null){
                    queue.offer(node.left);
                }
                if (node.right!=null){
                    queue.offer(node.right);
                }
            }
        }
        return count;
    }
}