目录
- 1 K-摇臂赌博机
- 2 ϵ \epsilon ϵ-贪心算法
- 3 softmax算法
- 4 Python实现与分析
1 K-摇臂赌博机
单步强化学习是最简单的强化学习模型,其以贪心策略为核心最大化单步奖赏
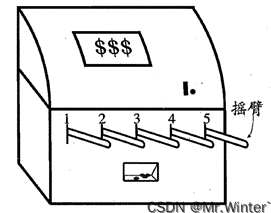
如图所示,单步强化学习的理论模型是 K K K-摇臂赌博机( K K K-armed bandit),描述如下: K K K-摇臂赌博机有 K K K个摇臂,赌徒在投入一个硬币后可选择按下其中一个摇臂,每个摇臂以一定的概率吐出硬币(硬币数量来自一个赌徒未知的概率分布),因此仅通过一次试验并不能确切地了解摇臂的奖赏期望,赌徒的目标是通过一定的策略最大化自己的奖赏,即获得最多的硬币。 K K K-摇臂赌博机问题抽象为强化学习任务后,摇臂即为某个状态下对应的 K K K个动作;硬币即为该状态下执行某动作后的奖赏值
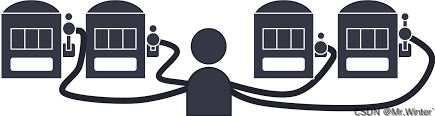
针对 K K K-摇臂赌博机问题有两种思路:
- 仅探索法(exploration-only):将所有的尝试机会平均分配给每个摇臂,即轮流按下每个摇臂若干次,最后以每个摇臂各自的平均吐币数作为奖赏期望的近似估计;
- 仅利用法 (exploitation-only):按下目前最优的——到目前为止平均奖赏最大的摇臂,若有多个摇臂同为最优,则从中随机选取一个
以上两种思路相互矛盾,构成强化学习所面临的探索-利用窘境(Exploration-Exploitation dilemma):仅探索法能很好地估计每个摇臂的性能,却会失去很多选择最优摇臂的机会;仅利用法局部性能较好,但因为过于贪心无法衡量各个摇臂,因此很可能选不到最优摇臂。这两种思路都难以使最终的累积奖赏最大化,欲使累积奖赏最大,则必须在探索与利用之间达成较好的折中。
将 K K K-摇臂赌博机应用在离散状态空间、动作空间上一般强化学习任务的方式是:将每个状态上动作的选择看作一个 K K K-摇臂赌博机问题,对每个状态分别记录各动作的尝试次数、当前平均累积奖赏等信息,训练一定次数后,即可基于赌博机算法进行动作决策。但是这种做法没有考虑强化学习任务马尔科夫决策过程的结构,具有局限性
2 ϵ \epsilon ϵ-贪心算法
ϵ \epsilon ϵ-贪心算法基于一个概率 ϵ \epsilon ϵ来对探索和利用进行折中:每次尝试时以 ϵ \epsilon ϵ的概率进行探索,此时以均匀概率随机选取一个动作;以 1 − ϵ 1-\epsilon 1−ϵ的概率进行利用,此时选择当前平均奖赏最高的动作(若有多个,则随机选取一个)。若动作奖赏的不确定性较大则需更多的探索,此时需要较大的 ϵ \epsilon ϵ值;反之若动作奖赏的不确定性较小,则少量的尝试就能很好地近似真实奖赏,此时需要较小的 ϵ \epsilon ϵ值即可。通常可令 ϵ \epsilon ϵ随尝试次数的增加而逐渐减小,例如令
ϵ = 1 / t \epsilon ={{1}/{\sqrt{t}}} ϵ=1/t

3 softmax算法
Softmax算法基于当前已知的动作平均奖赏来对探索和利用进行折中:若各动作的平均奖赏相当,则选取各动作的概率也相当;若某些动作的平均奖赏明显高于其他动作,则它们被选取的概率也明显更高。其中温度 τ > 0 \tau >0 τ>0趋于0算法趋于仅利用;趋于无穷大算法趋于仅探索。

4 Python实现与分析
首先我们先模拟一个 K K K-摇臂赌博机
class Bandit:
def __init__(self) -> None:
self.k = 0
self.handler = []
# @breif:添加摇臂
def addHandler(self, pList, vList):
h = BanditHandler(pList, vList)
self.handler.append(h)
self.k = self.k + 1
# @breif:删除摇臂
def delHandler(self, i):
if i > self.k - 1:
print("handler index i is invalid! i should be less than k!")
else:
self.handler.pop(i)
self.k = self.k - 1
# @breif: 选择摇臂i并弹出奖赏
def getReward(self, i):
if i > self.k - 1:
print("handler index i is invalid! i should be less than k!")
else:
return self.handler[i].pull()
接着实现上述的四种算法
-
仅探索法
def explorationOnly(self, T): # 累计奖赏 r = 0 rList = [] # 完全随机选取摇臂 for i in range(T): hIndex = random.randint(0, self.kBandit.k - 1) r = r + self.kBandit.handler[hIndex].pull() rList.append(r / (i + 1)) return rList -
仅利用法
def exploitationOnly(self, T): # 累计奖赏 r = 0 rList = [] # 各摇臂平均奖赏初始化 g = [0 for i in range(self.kBandit.k)] # 各摇臂选中次数初始化 count = [0 for i in range(self.kBandit.k)] for i in range(T): hIndex = g.index(max(g)) v = self.kBandit.handler[hIndex].pull() r = r + v g[hIndex] = (g[hIndex] * count[hIndex] + v) / (count[hIndex] + 1) count[hIndex] = count[hIndex] + 1 rList.append(r / (i + 1)) return rList -
ϵ \epsilon ϵ-贪心算法
def eGredy(self, T, e): # 累计奖赏 r = 0 rList = [] # 各摇臂平均奖赏初始化 g = [0 for i in range(self.kBandit.k)] # 各摇臂选中次数初始化 count = [0 for i in range(self.kBandit.k)] for i in range(T): if random.random() < e: hIndex = random.randint(0, self.kBandit.k - 1) else: hIndex = g.index(max(g)) v = self.kBandit.handler[hIndex].pull() r = r + v g[hIndex] = (g[hIndex] * count[hIndex] + v) / (count[hIndex] + 1) count[hIndex] = count[hIndex] + 1 rList.append(r / (i + 1)) return rList
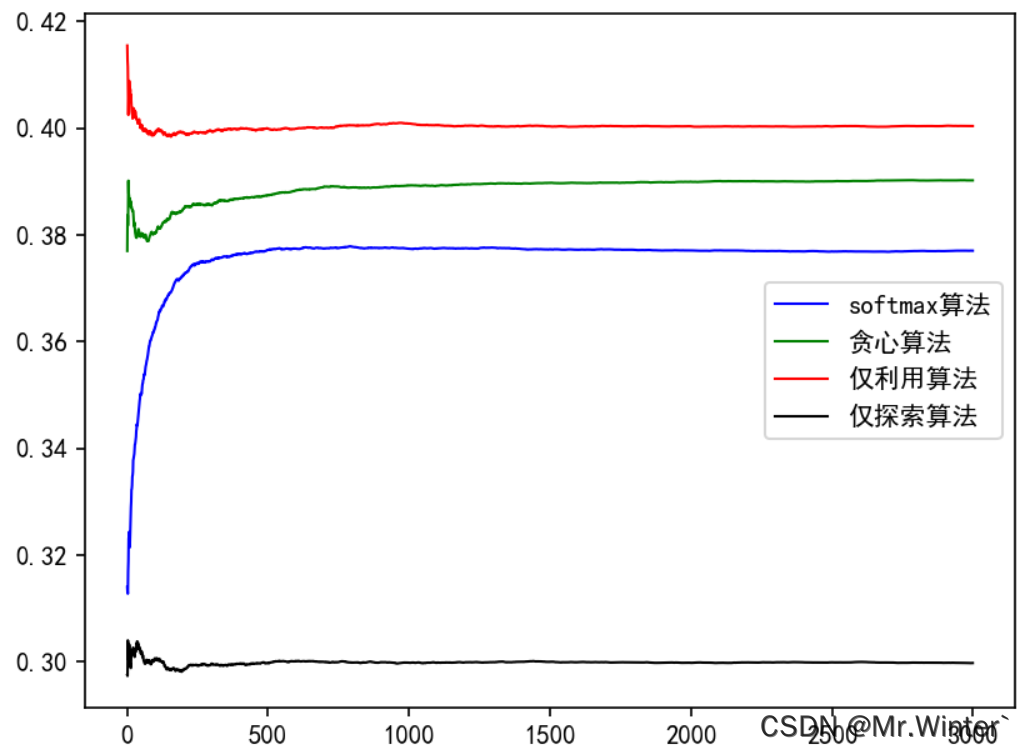
在本案例中,各个算法计算迭代若干次后的平均奖励曲线如图所示
本文完整工程代码请通过下方名片联系博主获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …