集成学习中结合策略

结合策略

• 学习器结合可能会从三个方面带来好处[Dietterich，2000]
  • 从统计的方面来看,由于学习任务的假设空间往往很大,可能有多个假设在训练集上达到同等性能,此时若使用单学习器可能因误选而导致泛化性能不佳,结合多个学习器则会减小这一风险;
  • 从计算的方面来看,学习算法往往会陷入局部极小,有的局部极小点所对应的泛化性能可能很糟糕,而通过多次运行之后进行结合,可降低陷入糟糕局部极小点的风险;
  • 从表示的方面来看,某些学习任务的真实假设可能不在当前学习算法所考虑的假设空间中,此时若使用单学习器则肯定无效,而通过结合多个学习器,由于相应的假设空间有所扩大,有可能学得更好的近似.
• 假定某集成包含T个学习器$h_1,h_2,\cdots ,h_T$,其中$h_i$在示例$\mathbf{x}$上的输出为$h_i(\mathbf{x})$

平均法

• 对数值型输出$h_i(\mathbf{x})\in \mathbb{R}$,最常见的结合策略是使用平均法(averaging)

简单平均法

• $$H(\mathbf{x})=\frac{1}{T}\sum _{i=1}^T{h}_i(\mathbf{x})$$

加权平均法

• 加权平均法(weighted averaging,WA)

  • $$H(\mathbf{x})=\sum _{i=1}^T{w}_i{h}_i(\mathbf{x})$$

  • $w_i$是个体学习器$h_i$的权重,通常要求$w_i⩾0$,${\sum }_{i=1}^T{w}_i=1$

    • 相关研究表明,必须使用非负权重才能确保集成性能一定由于单一最佳个体学习器
    • 因此集成学习中,一般对学习器的权重施加非负约束

  • 简单平均法是加权平均法的一个特例($w_i=\frac{1}{T}$)

  • 集成学习中的各种结合方法都可以视为其特例或变体

  • 对于给定的基学习器,不同的集成学习方法可以视为通过不同的方式来确定加权平均法中的基学习器权重

    • 例如估计出个体学习器的误差,然后令权重大小和误差大小成反比

  • 加权平均法的权重一般是从训练数据中学习得到,由于现实任务中的样本训练通常不充分(或存在噪声),使得学习得到的权重不完全可靠.对于规模较大的集成来说,学习的权重比较多,容易导致过拟合.

  • 基于上述情况,实验和应用中,加权平均法未必由于简单平均法

• 一般地,个体学习器性能相差较大时,适合采用加权平均法,个体学习器性能接近时,适合采用简单平均法

投票法

• 对于分类任务来说,学习器$h_i$将从分类别标记集合 { c 1 , c 2 , ⋯   , c N } \{c_1,c_2,\cdots,c_N\} {c1​,c2​,⋯,cN​}中预测出一个标记
• 最常见的学习器结合策略时使用投票法(voting)
• 不妨将$h_i$在样本$\mathbf{x}$上的预测输出表示为一个N维向量$(h_i^1(\mathbf{x});h_i^2(\mathbf{x});\cdots ;h_i^N(\mathbf{x}))$
  • 其中$h_i^j(\mathbf{x})$表示$h_i$在类别$c_j$上的输出

绝对多数投票法MV

• 绝对多数投票法(majority voting,有时简写为voting)

• $$H(\mathbf{x})=\{\begin{array}{ll}{c}_j,& \text{if }{\sum }_{i=1}^T{h}_i^j(\mathbf{x})>0.5{\sum }_{k=1}^N{\sum }_{i=1}^T{h}_i^k(\mathbf{x})\\ \text{reject},& \text{otherwise}\end{array}$$

• 总结为:若某标记$c_k$得票超过半数,则预测为$c_k$;否则拒绝预测

相对多数投票法PV

• 相对多数投票法(plurality voting)

• $$H(\mathbf{x})=c_{\underset{j}{\mathrm{argmax}}{\sum }_{i=1}^T{h}_i^j(\mathbf{x})}$$

  • H预测为得票最多的标记
  • 如果同时又多个标记获得最高票,则从中随机选取一个

加权投票法WV

• weighted voting

• $$H(\mathbf{x})=c_{\underset{j}{\mathrm{argmax}}{\sum }_{i=1}^T{w}_i{h}_i^j(\mathbf{x})}$$

  • 与加权平均法类似,$w_i$是$h_i$的权重
  • 通常$w_i⩾0$,${\sum }_{i=1}^T{w}_i=1$

小结

• 标准的绝对多数投票法提供了拒绝预测的选项(可能情况),在要求高可靠性的学习任务中是一个有用的机制
• 如果学习任务要求必须提供预测结果,则绝对投票法退化为相对多数投票法
  • 因此,这类任务中,绝对多数,相对多数投票法统称为多数投票法

其他投票法技巧

• 在现实任务中,不同类型个体学习器可能差生不同类型的$h_i^j(\mathbf{x})$值:
  • 类标记: h i j ( x ) ∈ { 0 , 1 } h_i^j(\boldsymbol{x})\in\{0,1\} hij​(x)∈{0,1}
    • 若$h_i$将类样本预测为$c_j$类别,则$h_i^j(\mathbf{x})$取1,否则为0
    • 这类投票称为硬投票(hard voting)
  • 类概率:$h_i^j(\mathbf{x})\in [0,1]$
    • 相当于对后验概率$P(c_j|\mathbf{x})$的一个估计
    • 这类投票方法称为软投票(soft voting)
• 不同类型的$h_i^j(\mathbf{x})$值不能混用,对一些能在预测出类别标记的同时产生分类置信度的学习器,其分类置信度可转化为类概率使用．
  • 若此类值未进行规范化,例如支持向量机的分类间隔值,则必须使用一些技术如
    • Platt 缩放(Platt scaling)[Platt，2000]
    • 等分回归(isotonic regression)[Zadrozny andElkan，2001]
    • 等方法进行“校准”(calibration)后才能作为类概率使用．
  • 虽然分类器估计出的类概率值一般都不太准确,但基于类概率进行结合却往往比直接基于类标记进行结合性能更好
  • 若基学习器的类型不同,则其类概率值不能直接进行比较;
    • 在此种情形下,通常可将类概率输出转化为类标记输出
    • 例如将类概率输出最大的$h_i^j(\mathbf{x})$设为1,其他设为0,然后再投票.

学习法

• 当训练数据很多时，一种更为强大的结合策略是使用“学习法”,即通过另一个学习器来进行结合.
• stacking方法是一种典型的方法,不能说stakcing完全等于同于学习法.

Stacking

• Stacking [Wolpert,1992; Breiman,1996b]是学习法的典型代表.(stacking本身也是一种集成学习方法)
• 这里我们把个体学习器(基础学习器)称为初级学习器.
• 用于结合的学习器称为次级学习器或元学习器(meta-learner).
• Stacking 先从初始数据集训练出初级学习器,然后“生成”一个新数据集
  • 在这个新数据集中,初级学习器的输出被当作样例输入特征,而初始样本的标记仍被当作样例标记.
  • 新数据集用于训练次级学习器.

伪代码

• 假定初级学习器使用不同学习算法产生,即初级集成是异质的.

• input:

  • 训练集$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\cdots ,({\mathbf{x}}_m,y_m)\}$
  • 初级学习算法${\mathfrak{L}}_1,{\mathfrak{L}}_2,\cdots ,{\mathfrak{L}}_T;$
  • 次级学习算法$\mathfrak{L}$

• $$\begin{array}{rl}& 01:\text{for }t=1,2,\dots ,T\text{do}\\ & 02:h_t={\mathfrak{L}}_t(D);\\ & 03:\text{end for}\\ & 04:D^{\prime }=\varnothing ;\\ & 05:\text{for }i=1,2,\dots ,m\text{ do}\\ & 06:\text{for }t=1,2,\dots ,T\text{ do}\\ & 07:z_{it}=h_t({\mathbf{x}}_i);\\ & 08:\text{end for}\\ & 09:D^{\prime }=D^{\prime }\cup ((z_{i1},z_{i2},\dots ,z_{iT}),y_i);\\ & 10:\text{end for}\\ & 11:h^{\prime }=\mathfrak{L}(D^{\prime });\end{array}$$

• $$H(\mathbf{x})=h^{\prime }(h_1(\mathbf{x}),h_2(\mathbf{x}),\dots ,h_T(\mathbf{x}))$$

• comments:

  • 1-3:使用初级学习算法${\mathfrak{L}}_t$产生初级学习器$h_t$
  • 4-10:生成次级训练集
  • 11:在${\mathcal{D}}^{\prime }$上使用次级学习算法$\mathfrak{L}$产生次级学习器$h^{\prime }$

• 在训练阶段,次级训练集是利用初级学习器产生的,若直接用初级学习器的训练集来产生次级训练集,则过拟合风险会比较大;

• 因此,一般是通过使用交叉验证或留一法这样的方式,用训练初级学习器未使用的样本来产生次级学习器的训练样本．

次级训练集的生成🎈

• 以k折交叉验证为例

  • 初始训练集$D$被随机划分为k个大小相似的集合$D_1,D_2,\cdots ,D_k$

  • 令$D_j$和$\overline{D_j}=D\backslash D_j$分别表示第$j$折的测试集和训练集.

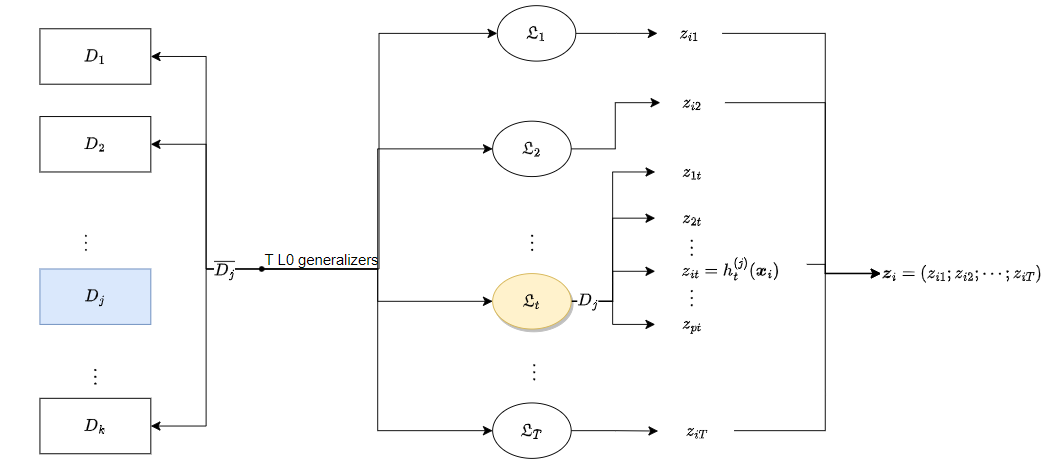
  • 给定$T$个初级学习算法,初级学习器$h_t^{(j)}$通过在$\overline{D_j}$上使用第$t$个学习算法而得.

  • 对$D_j$(测试集)中每个样本${\mathbf{x}}_i$,令 $z_{it}=h_t^{(j)}({\mathbf{x}}_i)$，($i$表示$D_j$的第$i$个样本,而t表示第t个学习算法,设$D_j$中含有$p\approx m/k$个样本,由于交叉验证完成后所有样本都等完成映射，$p$值仅做参考)

  • 则由${\mathbf{x}}_i$所产生的次级训练样例的示例部分为${\mathbf{z}}_i=(z_{i1};z_{i2};\cdots ;z_{iT})$，标记部分为$y_i$(注意到,此时示例的维数此时是$T$,和初级学习器的个数一致)，示例维数变换关系：${\mathbf{x}}_i\in {\mathbb{R}}^U\to {\mathbf{z}}_i\in {\mathbb{R}}^T$，其中$U$表示初级训练集示例的维数。

    • $${\mathbf{x}}_i\in {\mathbb{R}}^U\to {\mathbf{z}}_i\in {\mathbb{R}}^T$$

  • 在整个交叉验证过程结束后,从这T个初级学习器产生的次级训练集是$D^{\prime }=\{({\mathbf{z}}_i,y_i){\}}_{i=1}^m$,然后$D^{\prime }$将用于训练次级学习器.

  • 

• 次级学习器的输入属性表示和次级学习算法对Stacking集成的泛化性能有很大影响.

  • 有研究表明,将初级学习器的输出类概率作为次级学习器的输入属性,用多响应线性回归(Multi-response Linear Regression，简称MLR)作为次级学习算法效果较好[Ting and Witten，1999]
  • MLR是基于线性回归的分类器，它对每个类分别进行线性回归，属于该类的训练样例所对应的输出被置为1，其他类置为0;测试示例将被分给输出值最大的类.
    WEKA中的StackingC算法就是这样实现的.
  • 在 MLR中使用不同的属性集更佳[Seewald, 2002].

refs@更多集成学习相关参考

• <<人工智能：现代方法(斯图尔特·罗素) >>
• <<python机器学习基础教程>>
  • 在决策树集成一节中介绍了randomForest和GradientBoosting

Skearn中的集成学习引言

摘要

• The goal of ensemble methods is to combine the predictions of several base estimators built with a given learning algorithm in order to improve generalizability / robustness over a single estimator.

• Two families of ensemble methods are usually distinguished:

  • In averaging methods, the driving principle is to build several estimators independently and then to average their predictions. On average, the combined estimator is usually better than any of the single base estimator because its variance is reduced.

    Examples: Bagging methods, Forests of randomized trees, …

  • By contrast, in boosting methods, base estimators are built sequentially and one tries to reduce the bias of the combined estimator. The motivation is to combine several weak models to produce a powerful ensemble.

    Examples: AdaBoost, Gradient Tree Boosting, …

翻译1

• 集成学习的目标是将使用给定学习算法构建的多个基估计器的预测结果结合起来，以提高对单个估计器的泛化性和鲁棒性。

• 通常区分两类集成方法：

  • 在平均方法中，主要原理是独立构建多个估计器，然后对它们的预测结果进行平均。平均而言，组合估计器通常优于任何单个基估计器，因为其方差降低了。
    • 例如：Bagging 方法、随机森林等。
  • 相比之下，在提升方法中，基估计器是顺序构建的，以尝试降低组合估计器的偏差。动机是将多个弱模型组合成一个强大的集成模型。
    • 例如：AdaBoost、梯度提升树等。

翻译2

• 集成方法 的目标是把多个使用给定学习算法构建的基估计器的预测结果结合起来，从而获得比单个估计器更好的泛化能力/鲁棒性。

• 集成方法通常分为两种:

  • 平均方法，该方法的原理是构建多个独立的估计器，然后取它们的预测结果的平均。一般来说组合之后的估计器是会比单个估计器要好的，因为它的方差减小了。

    示例: Bagging 方法 , 随机森林 , …

  • 相比之下，在 boosting 方法 中，基估计器是依次构建的，并且每一个基估计器都尝试去减少组合估计器的偏差。这种方法主要目的是为了结合多个弱模型，使集成的模型更加强大。

    示例: AdaBoost , 梯度提升树 , …