CMU15-445 2022 Fall 通关记录 —— Project 2：B+ Tree（上篇）

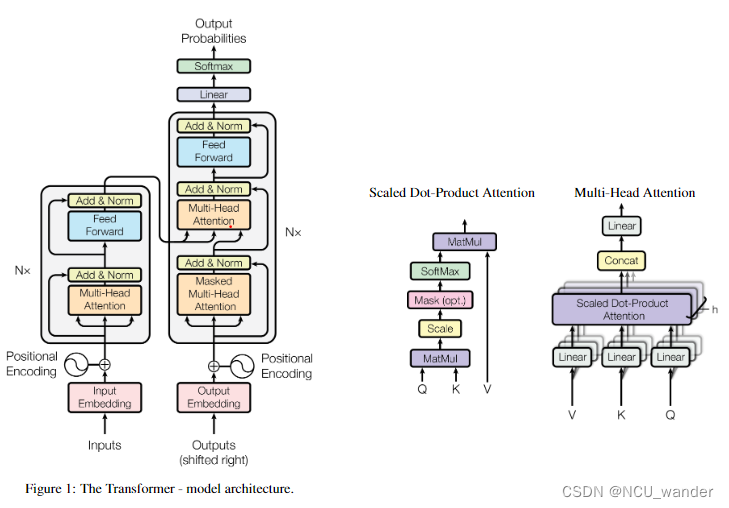
Project 2：B+ Tree

Project #2 - B+Tree | CMU 15-445/645 :: Intro to Database Systems (Fall 2022)

NOTE：

记录完成该Pro中，一些可能会遇到的问题：

本实验中，有很多API是需要自己去实现的，因此，我推荐把逻辑梳理清楚后，再尝试去实现，函数设计是一门学问，我个人地原则是尽量避免出现重复代码段，即相同地处理置于一个函数中；
相较于Pro0和Pro1，本次指导书中的内容简略了许多，格外要注意到底是在哪实现代码，例如Task2是在src/include/storage/index/b_plus_tree.h和相应的CPP文件中实现（为什么会这么说？因为我就犯蠢了）
官方提供了一个可以正确打印实现的B+树的网页，可以用于检测与本地实现之间的差异，推荐在实现具体函数地时候可以先手动尝试一下插入、删除等操作。

BusTub B+Tree Printer (cmu.edu)
本次实验的实现中，涉及到了很多与迭代器相关的操作，包括但不限于std::prev\ std::next\ std::lower_bound \ std::move_backwrad()，所以我认为可以提前了解一下C++提供的这些语法糖，还能使你的code能力得到一定的提升。推荐网站：cppreference.com
每次用完Page后记得Unpin！
我在进行这次实验的时候，短暂地尝试了使用Copliot来辅助完成编写，可以省去很多简单逻辑的重复编写，但是有些细节逻辑处理的仍不是特别好，或者是有可能是我没有理解AI的意思。
虽然在我下文中地描述中使用了内部页和叶子页这种比较蹩脚地称呼，但是还是要意识到本质上依旧是树中地一个节点，为了方便，在代码中给变量取名地时候可以用page和node加以区分。

Task #1：B+ Tree Pages

本任务中需要实现三个Page类：

B+ Tree Parent Page

即下面这两个 Page 的父类
B+ Tree Internal Page
B+ Tree Leaf Page

在完成这三个类之前，我认为应当有必要详细了解一下B+ 树的特点，虽然课程中也有提到，但是比较浅显，此处放一篇知乎上的高赞文章，应当可以从前世今生了解一下B+树：

平衡二叉树、B树、B+树、B*树理解其中一种你就都明白了 - 知乎 (zhihu.com)

下面这篇文章则是详细介绍了B+树中发生插入、删除等操作时的逻辑：

B树和B+树的插入、删除图文详解 - nullzx - 博客园 (cnblogs.com)

总而言之，B+树需要仅在叶子结点存储数据，而非叶子结点则是用于索引。难度最大的点在于插入与删除操作时，节点对应的分裂与合并操作。

B+ Tree Parent Page

没什么可说的，都是些辅助函数，但是可以从结构上明确下，方便后面的设计。

虽然上一个实验已经接触到了Page，但是也就是通过page_id索引对应的Page而已，不需要关注Page的内容。实际上，Page中的相关变量如下：

/** The actual data that is stored within a page. */
char data_[BUSTUB_PAGE_SIZE]{};
/** The ID of this page. */
page_id_t page_id_ = INVALID_PAGE_ID;
/** The pin count of this page. */
int pin_count_ = 0;
/** True if the page is dirty, i.e. it is different from its corresponding page on disk. */
bool is_dirty_ = false;
/** Page latch. */
ReaderWriterLatch rwlatch_;

其中存储了 BUSTUB_PAGE_SIZE = 4096(Bytes)大小的数据，剩余成员变量即一些相关信息，可以称为metadate，即元数据。

而B_PLUS_TREE_PAGE则存储了24Bytes的相关信息，可以理解为通用的头信息，如下所示：

IndexPageType page_type_;   // leaf or internal. 4 Byte
lsn_t lsn_  // temporarily unused. 4 Byte
int size_;  // tree page data size(not in byte, in count). 4 Byte
int max_size_;  // tree page data max size(not in byte, in count). 4 Byte
page_id_t parent_page_id_; // 4 Byte
page_id_t page_id_; // 4 Byte

通过引用的头文件

#include "buffer/buffer_pool_manager.h"

可以看出，在本项目中会通过上一个Pro中实现的Buffer Pool来管理Page。

此处我有一个疑问，B+树中的头信息，会占据Page 原本用于存放数据的空间吗？

B+ Tree Internal Page

Internal Page，每个Page中存储的是 N 个索引以及 N+1 个指向子树的指针

从本实验开始，难度逐渐加大，一个重要原因就在于本实验只提供了一些最基础的API，剩余的API都需要自己设计。

此处仍需要先明确一下，我们实现的B+树是一种模板编程，bustub中提供的索引模板参数定义如下：

#define INDEX_TEMPLATE_ARGUMENTS template <typename KeyType, typename ValueType, typename KeyComparator>

我们要根据Key值来找到对应的索引位置，即K(i) <= K < K(i+1)，而KeyComparator则是提供了一种比较Key值的手段，因为KeyType不一定是可以直接比较大小的类型。

而映射类型则为：

#define MappingType std::pair<KeyType, ValueType>

根据代码中，对于INTERNAL_PAGE_SIZE的定义，一个Page的结构如下图所示，此处也回答了我此前的疑问，Page中原本用于存储键值对的内存空间，分出了24Bytes给B+树节点的头信息。

代码中最怪的地方，应当在于私有变量仅有一个：

// Flexible array member for page data.
MappingType array_[1];

从表面上我们可以看出，这是一个大小为1的数组，元素为键值对，按理来说，知道内部页可用于存放数据的空间大小和键值对的大小，就可以计算出有多少键值对可以放入一个Page中，但定义只有一个元素显然不合理。

经查询相关博客与询问GPT之后，明白了为什么要这么做的原因：

做个数据库：2022 CMU15-445 Project2 B+Tree Index - 知乎 (zhihu.com)

GPT将Flexible array翻译为柔性数组，必须要放在结构体的最后，用以占用结构体中剩余的未被定义的内存空间，即该数组可以实现动态扩张，内部页的内存结构如下：

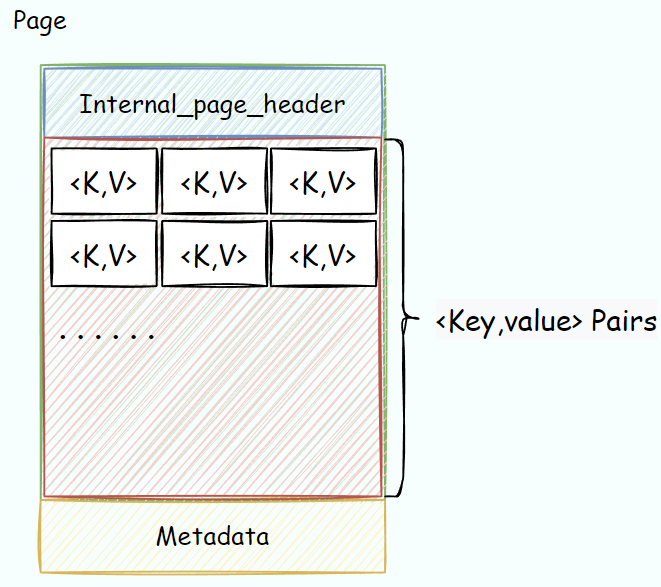
博客中提到了一点，即内存对齐问题，因为头信息中的所有数据都是4Bytes，而在同一棵树中，每一个键值对的大小也是固定的，是满足内存对齐的条件的。我稍微想了一下，如果有一个头信息占用的空间过大，会导致数据空间以该变量的大小来决定，键值对儿则未必能满足对齐条件。只要键值对类型的占用空间 ≥ 4Bytes，或者是 4Bytes = 整数倍的键值对大小，理应都是可以满足对齐条件的。这也正好给内存对齐提供了一个实例。此处如有错误，希望各位能在评论区中指出。

而指导中也提出了一点，第一个key的位置是不存放数据的，因此内部页的逻辑结构则如下面两张图所示：

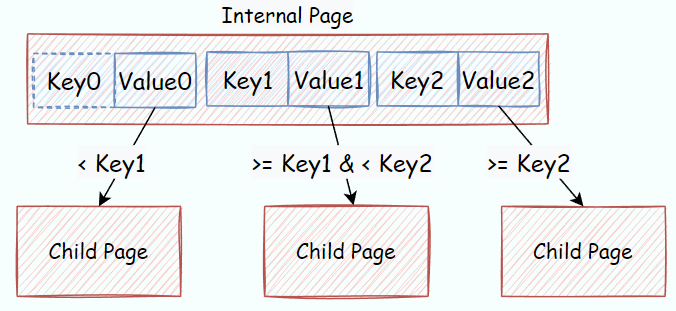
本Task需要完成的API有如下几个：

void Init(page_id_t page_id, page_id_t parent_id = INVALID_PAGE_ID, int max_size = INTERNAL_PAGE_SIZE);

auto KeyAt(int index) const -> KeyType;
void SetKeyAt(int index, const KeyType &key);
auto ValueAt(int index) const -> ValueType;

仍是一些辅助函数，实现起来并不困难。

B+ Tree Leaf Page

叶子页的内部结构和内部页是近似的，无非是value部分存储的是数据，而且多了一个变量next_page_id_指向下一个Page的ID。

其逻辑结构如下所示：

指导书中也点明了叶子页中value should only be 64-bit record_id that is used to locate where actual tuples are stored, see RID class defined under in src/include/common/rid.h. 在这里只需要理解值是RID就可以了，更深刻一点可以理解为二级索引指向具体数据的指针，因为RID就是个64位的整数。

叶子页需要实现的API则如下所示：

void Init(page_id_t page_id, page_id_t parent_id = INVALID_PAGE_ID, int max_size = LEAF_PAGE_SIZE);
// helper methods
auto GetNextPageId() const -> page_id_t;
void SetNextPageId(page_id_t next_page_id);
auto KeyAt(int index) const -> KeyType;

仍是一些辅助函数，实现起来也不困难。

另外，指导书中也说明了，无论是内部页还是叶子页，都需要通过page_id获取缓冲池中内存页的数据内容，通过reinteroret cast转换成为内部页/叶子页。

此处不理解为什么要使用不安全的reinteroret cast（该强制类型转换用于转化指针和引用，但并不进行数据类型检查，因此不安全）。

补充

通过实例化的模板类可以看出，无论是内部页还是叶子页（以叶子页为例），其KeyValue = GenericKey，KeyComparator = GenericComparator，而通过这两个类的说明可知：

GenericKey使用一个固定长度的数组来保存用于索引的数据，其实际大小是通过模板参数指定和实例化的；其中提供了一个仅用于测试时的函数ToString()，可以将key强转为int_64类型。
GenericComparator的比较规则是左值 < 右值，返回 -1，左值 > 右值，返回 1，如果两者相等，则返回0。

Task #2：B+ Tree Data Structure（Insertion，Deletion，Point Search）

任务2应当是本节的重点。而且官方还提供了第一个CheckPoint，只需要完成插入，删除以及点查询三个功能即可.

下面这个网站可以实现B+树的可视化：

B+ Tree Visualization (usfca.edu)

指导书中提到了几个点：

B+树仅支持唯一索引，所以插入时，需要判断key是否存在，存在即返回false；且插入触发拆分条件（叶节点插入后的键/值对数等于 max_size ，内部节点插入前的子节点数等于 max_size ）时，则应正确执行拆分。
删除时，需要考虑当前页中元素数量小于阈值（内部页是max + 1 的一半，叶子页是一半），即需要考虑借元素或者合并操作。
以下为指导书中的原话：

由于任何写入操作都可能导致 B+Tree 索引中的 root_page_id 发生变化，因此您有责任更新标题页 ( src/include/storage/page/header_page.h ) 中的 root_page_id 。这是为了确保索引在磁盘上是持久的。在 src/include/storage/index/b_plus_tree.h的BPlusTree 类中，已经实现了一个名为 UpdateRootPageId 的函数；需要做的就是在 B+Tree 索引的 root_page_id 发生变化时调用此函数。

本实验的相关API就需要自己实现了。而指定的GetValue()、Insert()和Delete()函数都是在b_plus_tree.cpp中实现的。

GetValue()

首先应当找到目标叶子节点，可以将搜索过程集成在FindLeaf()函数中，无论是在纯查询，还是插入或是删除，都用得着。搜寻要从根节点开始搜索：

在内部页中搜索，直到找到叶子页为止。

记住内部页中第一个key是不存在的，遍历方式采用二分查找即可（当然也有其他的实现方式）。找到第一个大于key的节点，返回前一个节点的value，即指向子树的指针；如果key相同，就说明找到了。
在叶子页中搜索，同样采用二分查找，将最终结果保存在形参的vector中。

此处需要注意，查找page需要借由Buffer Pool Manager来实现，即调用FetchPage()，当已经找到最终的value时，记得unpin叶子节点，否则运行过程中有可能出现Buffer Pool中的所有页都被pin住，无法加载新页进内存。

Insert()

先说一种特殊情况，即B+树为空，需要创建一个新的页作为根节点，此时根节点也是叶子。与根节点相关时，指导书中原话如下：

Since any write operation could lead to the change of root_page_id in B+Tree index, it is your responsibility to update root_page_id in the header page (src/include/storage/page/header_page.h). This is to ensure that the index is durable on disk. Within the BPlusTree class, we have already implemented a function called UpdateRootPageId for you; all you need to do is invoke this function whenever the root_page_id of B+Tree index changes.

即涉及到根节点的数据更新时，需要调用UpdateRootPageId()函数;

剩余的情况大体可以分三种，首先第一步都是在树中找对应的节点：

如果树中已存在key，则返回false，因为本Pro中仅讨论唯一索引；
如果是叶子节点，插入后：
- 如果页中元素个数<= m - 1，结束；
- 反之，元素个数> m - 1，则当前节点分裂为左右两个节点，前m/2个元素置于左节点，剩余的置于右节点，第m/2 + 1个元素上移至父节点中，其左Value指向左节点，右Value指向右节点。
如果是内部节点，插入后：
- 如果页中元素个数<= m - 1，结束；
- 反之，元素个数> m - 1，则当前节点分裂为左右两个节点，前(m-1)/2个元素置于左节点，后面的m-(m-1)/2个元素置于右节点，第m/2个元素上移至父节点中，其左Value指向左节点，右Value指向右节点，并继续判断父节点是否需要分裂。

Q：为什么内部页分裂的时候需要考虑传入Buffer Pool Manger呢？而叶子页分裂时不需要？

A：为了修改赋值后键值对子树的父节点的page_id，所以要取出分裂后页中每个键值对指向的子树页。

Delete() => Remove()

B+树删除的逻辑是有一张经典的伪代码图做解释的（可自行查询），相比较插入的逻辑，删除的逻辑大体上相当于是个逆过程，但是要考虑的情况却要多不少，难点就在于借节点和合并以保持B+树的结构上。大体逻辑如下：

树为空或者没有找到待删除的元素，直接返回
如果是叶子页
- 如果页中元素个数大于“一半”（此处至向上取整的最大值的一半 - 1，以5为例，就是 3 - 1 = 2），树的结构不会发生变化，直接返回即可
- 反之，有两种情况：
  - 若兄弟页（特指父页相同的兄弟页）的元素数量多于一半，则从中借一个元素：如果是左兄弟就搬最后一个元素到起始；如果是右兄弟就搬第一个元素到末尾。同时，用该节点替换父节点中的元素。
  - 反之，就要考虑将两个页进行合并操作，可以把源节点复制到兄弟节点里，也可以相反，但是要注意父节点中对应Value的删除，和page_id的更新。
如果是内部页
- 如果页中元素大于一半，则无需操作，直接结束即可
- 反之，和叶子页的逻辑一致，需要考虑的一个问题就是如果根页是内部页中仅剩下一个元素即只存在一个child的时候，就需要把这个child上升为根节点。另一种情况就是既是根又是叶子页的时候，直接就把元素删光了，也不是没可能的。

另外有一个很容易忽略的点，即合并两个页之后，是有一个page_id是要被删除的。你会发现已提供的API中存在一个参数为transaction即事务，其中提供了一个名为AddIntoDeletedPageSet的API，便是用于做这件事的：把那些待删除的的Page加入deleted_page_set_中，在删除操作的末尾，后续统一处理（可以采用遍历迭代器的方式进行删除）。

在提交前勿忘记检查一遍格式：

$ make format
$ make check-lint
$ make check-clang-tidy-p1

完成两个Task后即可尝试提交通过CheckPoint 1。

补充

本实验有两个辅助性工具，一个是对你自己实现的本地B+树进行可视化，参考指导书中Tree Visualization一节；另一个则是官方提供的BusTub B+Tree Printer (cmu.edu)云B+树可视化脚本。

通过这两个工具，可以验证你自己书写的B+树的结构是否一致，用以判断大致是哪里出了问题。