文章目录
- 主要技术栈
- 目的
- 实现步骤
- 1. 前端发送信息
- 2. 后端处理数据
- 3. 前端渲染数据
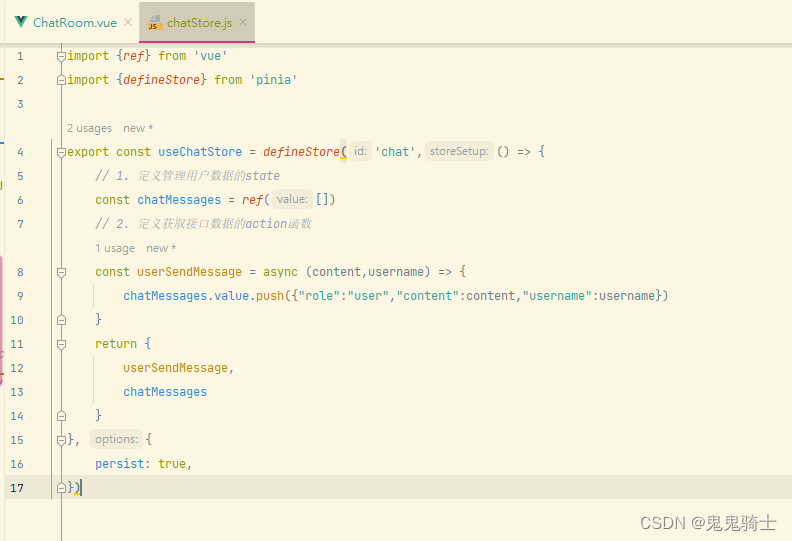
- 4. store
主要技术栈
主要技术栈是vue3,springboot,websocket,element-plus
目的
主要目的是复习和梳理
实现步骤
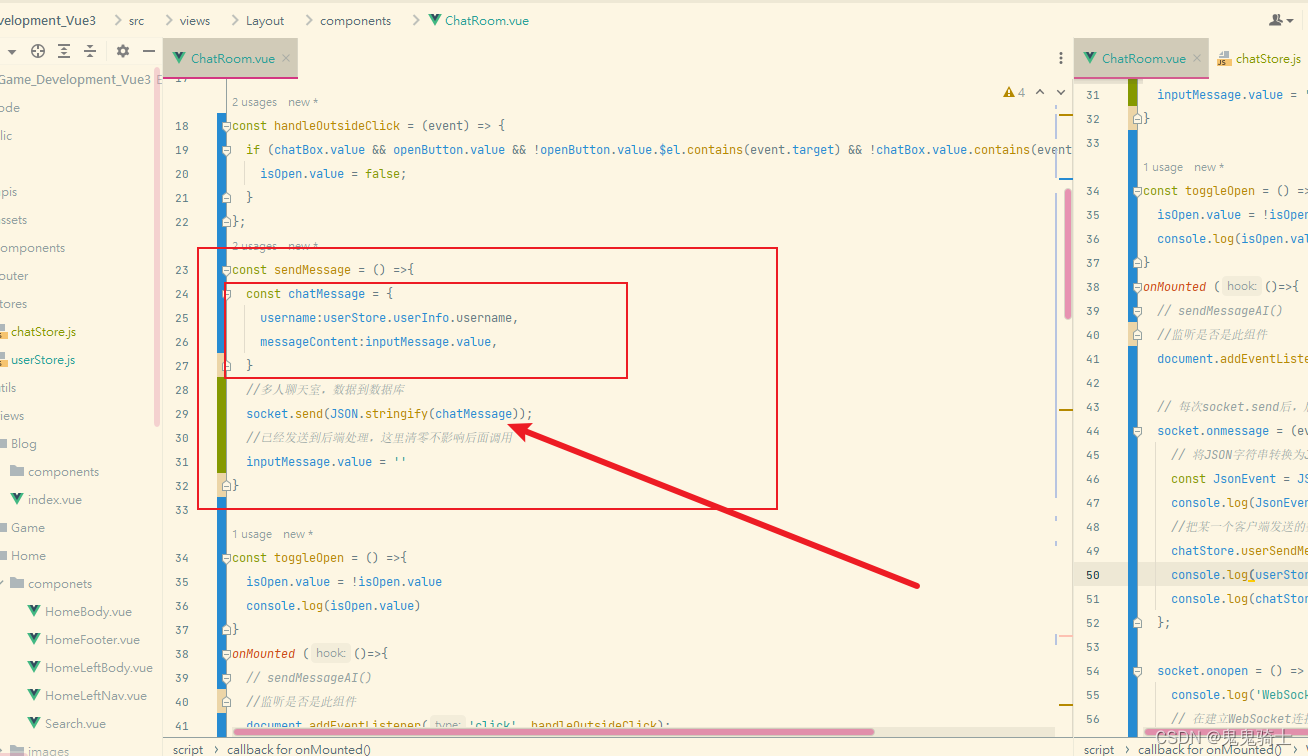
1. 前端发送信息
发送信息,包装信息,转json,用socket发送到后端,使输入栏清空
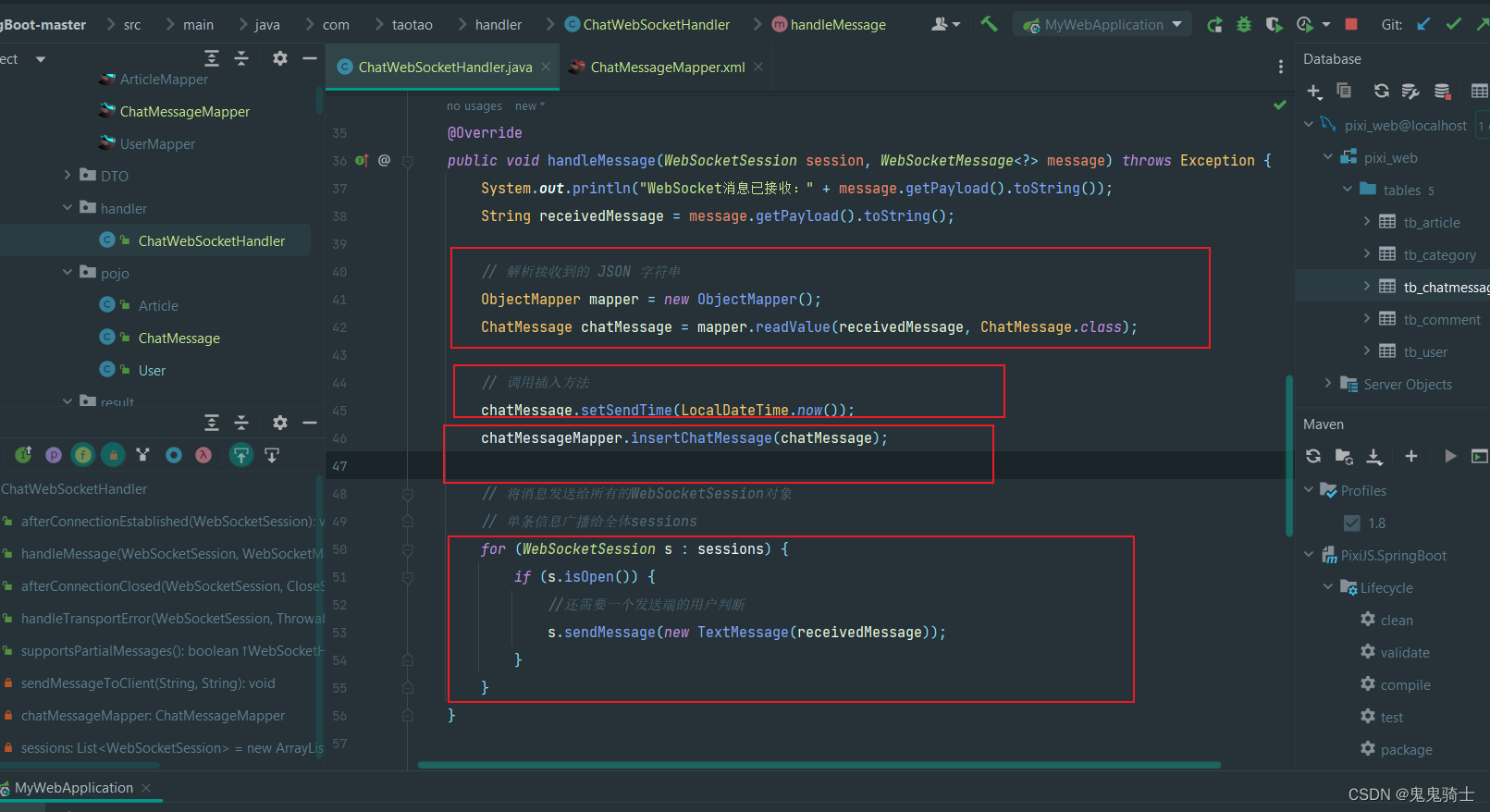
2. 后端处理数据
后端解析json,因为是socket接口,所以不能用@requestbody解析json,用以下方式解析json
设置发送时间为当前时间,然后执行mapper数据库插入
广播给所有的正在链接的socket,广播数据是json数据,带着user,和content,以便识别到底哪个客户端发送的信息
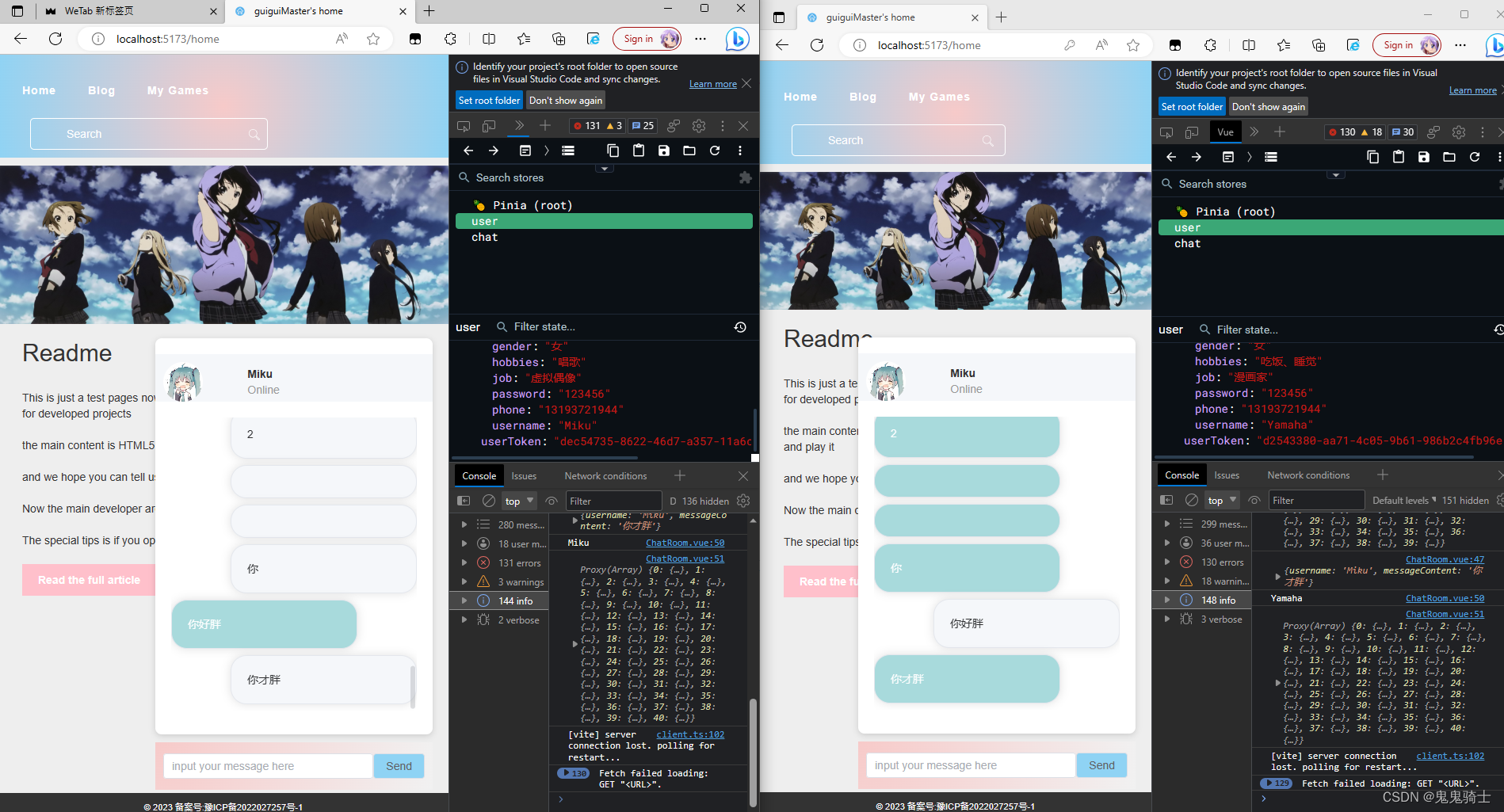
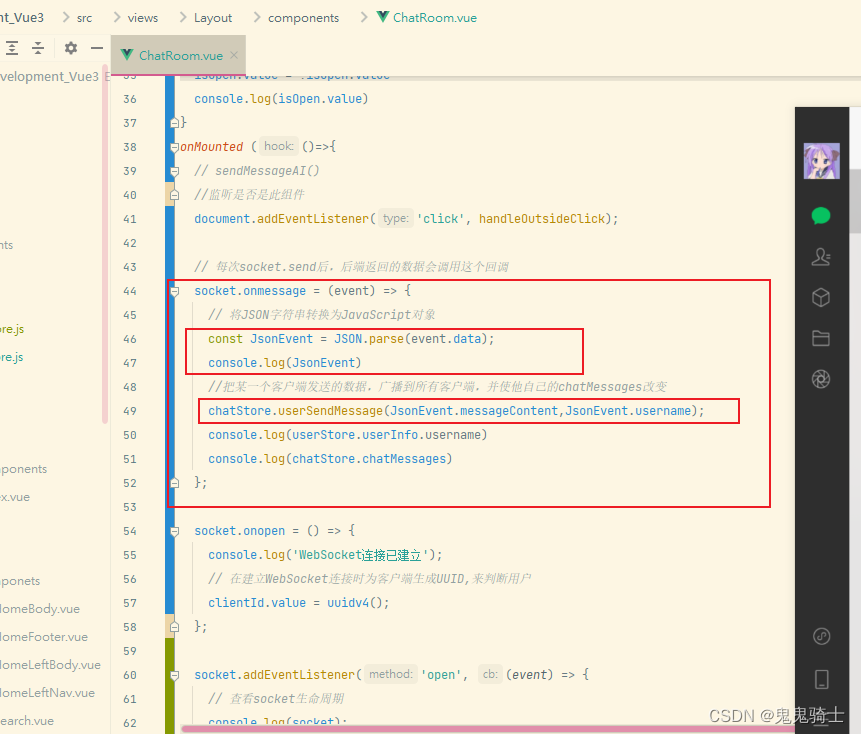
3. 前端渲染数据
在后端执行sendMessage方法后,前端执行回调,onmessage,将后端json转为对象,使用store来进行数据的插入管理,参数分别为content和username
4. store