代码仓库

https://github.com/phprao/go-graphic

变换

矩阵操作与向量操作：https://learnopengl-cn.github.io/01%20Getting%20started/07%20Transformations/

在OpenGL中，由于某些原因我们通常使用4×4的变换矩阵，而其中最重要的原因就是大部分的向量都是4分量的。

矩阵实际上就是一个数组

type Mat4 [16]float32

func Ident4() Mat4 {
	return Mat4{1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1}
}

向量的缩放

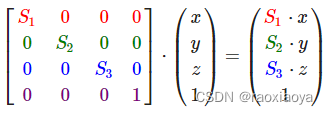
向量的位移

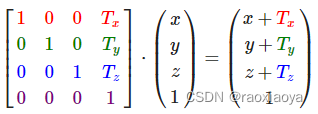
齐次坐标(Homogeneous Coordinates)

向量的w分量也叫齐次坐标。想要从齐次向量得到3D向量，我们可以把x、y、z坐标分别除以w坐标。我们通常不会注意这个问题，因为w分量通常是1.0。使用齐次坐标有几点好处：它允许我们在3D向量上进行位移（如果没有w分量我们是不能位移向量的）。

如果一个向量的齐次坐标是0，这个坐标就是方向向量(Direction Vector)，因为w坐标是0，这个向量就不能位移（译注：这也就是我们说的不能位移一个方向）。

有了位移矩阵我们就可以在3个方向x、y、z上移动物体，它是我们的变换工具箱中非常有用的一个变换矩阵。

向量的旋转

沿任意轴旋转

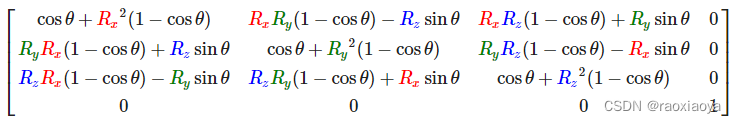
建议您在组合矩阵时，先进行缩放操作，然后是旋转，最后才是位移，否则它们会互相影响。

GLM是OpenGL Mathematics的缩写，GLM库从0.9.9版本起，默认会将矩阵类型初始化为一个零矩阵（所有元素均为0），而不是单位矩阵（对角元素为1，其它元素为0）。

对应golang中的包github.com/go-gl/mathgl/mgl32

// 生成一个向量
v4 = mgl32.Vec4{1, 1, 1, 1}
v3 = mgl32.Vec3{3, 3, 3}
v4 = v3.Vec4(1)
v2 = v3.Vec2()

// 向量的Add, Sub, Mul, Dot, Cross, Len

// 矩阵之间点乘
A.Mul4(B)

// 生成4*4的单位矩阵
model := mgl32.Ident4()

// 生成一个沿向量(3,4,5)移动的变换矩阵trans3d
/*
[1, 0, 0, 3]
[0, 1, 0, 4]
[0, 0, 1, 5]
[0, 0, 0, 1]
*/
trans3d := mgl32.Translate3D(3,4,5)
// 使向量vec3(1,2,3)沿着向量(3,4,5)移动
// 结果 (4,6,8)
mgl32.TransformCoordinate(mgl32.Vec3{1, 2, 3}, trans3d)

// 生成缩放比例(2,2,2)的变换矩阵
// 如果缩放的比例是负值，会导致图像翻转
/*
[2, 0, 0, 0]
[0, 2, 0, 0]
[0, 0, 2, 0]
[0, 0, 0, 1]
*/
scale3d := mgl32.Scale3D(2, 2, 2)
// 使向量vec3(1,2,3)缩放(2,2,2)
// 结果 (2,4,6)
mgl32.TransformCoordinate(mgl32.Vec3{1, 2, 3}, scale3d)

// 沿轴(3,3,3)旋转20度的变化矩阵
/*
[5.735343 2.588426 8.066097 0.000000]
[8.066097 5.735343 2.588426 0.000000]
[2.588426 8.066097 5.735343 0.000000]
[0.000000 0.000000 0.000000 1.000000]
*/
rotate3d := mgl32.HomogRotate3D(mgl32.DegToRad(20), mgl32.Vec3{3, 3, 3})
// 使向量vec3(1,2,3)沿轴(3,3,3)旋转20度
// 结果 (35.11049, 27.302063, 35.92665)
mgl32.TransformCoordinate(mgl32.Vec3{1, 2, 3}, rotate3d)

因为底层的math.Sin(angle)接受的是弧度radian，而不是度数degree，所以此处也要传弧度值，转换函数mgl32.RadToDeg() 和 mgl32.DegToRad()。

变换矩阵类型为mgl32.Mat4类型，我们使用uniform将其传入到着色器中

model := mgl32.Ident4()
modelUniform := gl.GetUniformLocation(program, gl.Str("model\x00"))
gl.UniformMatrix4fv(modelUniform, 1, false, &model[0])

uniform mat4 model;

示例：对现有纹理，实现先缩放，再旋转，再移动的效果

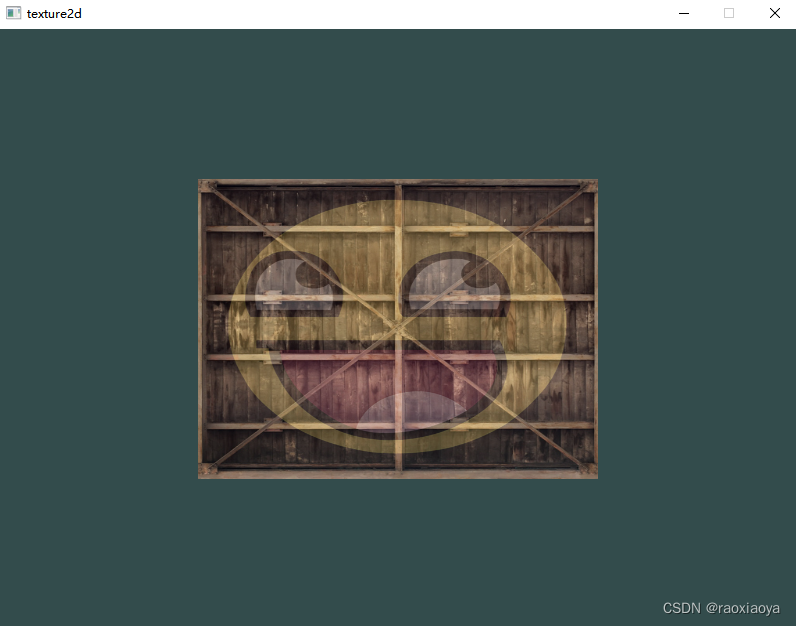
操作后效果

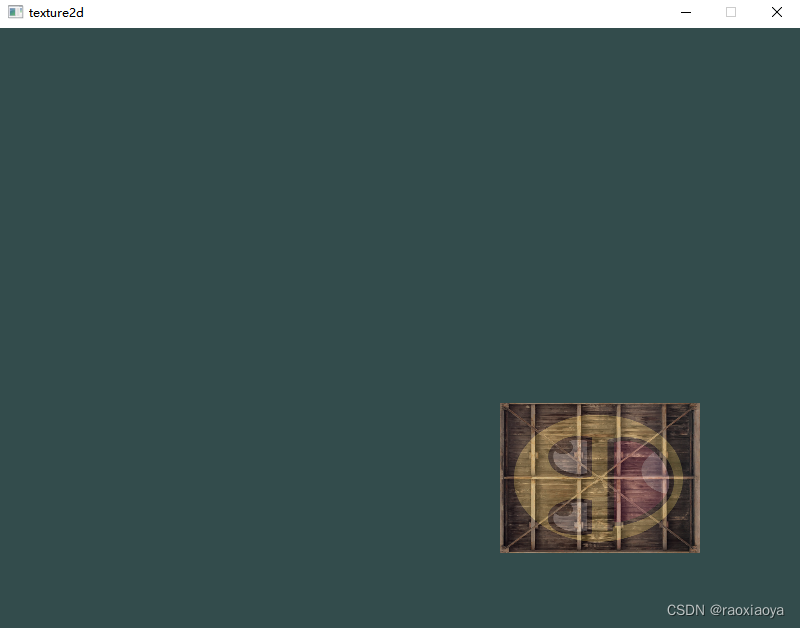
主要代码：

for !window.ShouldClose() {
    ......
    gl.UseProgram(program)

    rotate := mgl32.HomogRotate3D(mgl32.DegToRad(90), mgl32.Vec3{0, 0, 1})
    scale := mgl32.Scale3D(0.5, 0.5, 0.5)
    translate := mgl32.Translate3D(0.5, -0.5, 0)
    // 顺序要反着看：依次是 scale，rotate，translate
    transe := translate.Mul4(rotate).Mul4(scale)
    gl.UniformMatrix4fv(gl.GetUniformLocation(program, gl.Str("transe\x00")), 1, false, &transe[0])
    ......
}

顶点着色器

......
uniform mat4 transe;
......
void main() {
    gl_Position = transe * vec4(vPosition, 1.0);
    ......
}

我们可以让旋转的弧度随着时间变动，这样图像就旋转起来了

rotate := mgl32.HomogRotate3D(float32(glfw.GetTime()), mgl32.Vec3{0, 0, 1})

glfw.GetTime()返回的时间是从窗口创建开始计时的，单位是秒，数值如下：

0.19938110100045076
0.3682488961570842
0.8834820281800326
...
1.0471016692995818
1.2141550765655154
1.380787958668221
...

表示窗口运行了多少秒。

示例2：在一个窗口中画两个箱子，一个在不停旋转，一个在不停缩小放大

for !window.ShouldClose() {
    gl.ClearColor(0.2, 0.3, 0.3, 1.0)
    gl.Clear(gl.COLOR_BUFFER_BIT)
    gl.UseProgram(program)

    gl.ActiveTexture(gl.TEXTURE0)
    gl.BindTexture(gl.TEXTURE_2D, texture1)
    gl.Uniform1i(gl.GetUniformLocation(program, gl.Str("ourTexture1"+"\x00")), 0)

    gl.ActiveTexture(gl.TEXTURE1)
    gl.BindTexture(gl.TEXTURE_2D, texture2)
    gl.Uniform1i(gl.GetUniformLocation(program, gl.Str("ourTexture2"+"\x00")), 1)

    gl.BindVertexArray(vao)

    // 第一个箱子
    rotate := mgl32.HomogRotate3D(float32(glfw.GetTime()), mgl32.Vec3{0, 0, 1}) // 旋转效果
    scale := mgl32.Scale3D(0.5, 0.5, 0.5)
    translate := mgl32.Translate3D(0.5, -0.5, 0)
    transe := translate.Mul4(rotate).Mul4(scale)
    gl.UniformMatrix4fv(gl.GetUniformLocation(program, gl.Str("transe\x00")), 1, false, &transe[0])
    gl.DrawElements(gl.TRIANGLES, pointNum, gl.UNSIGNED_INT, gl.Ptr(indices))

    // 第二个箱子
    rotate2 := mgl32.HomogRotate3D(mgl32.DegToRad(90), mgl32.Vec3{0, 0, 1})
    s := float32(math.Sin(glfw.GetTime()))
    scale2 := mgl32.Scale3D(s, s, s)
    translate2 := mgl32.Translate3D(-0.5, 0.5, 0)
    transe2 := translate2.Mul4(rotate2).Mul4(scale2)
    gl.UniformMatrix4fv(gl.GetUniformLocation(program, gl.Str("transe\x00")), 1, false, &transe2[0])
    gl.DrawElements(gl.TRIANGLES, pointNum, gl.UNSIGNED_INT, gl.Ptr(indices))

    glfw.PollEvents()
    window.SwapBuffers()
}

---

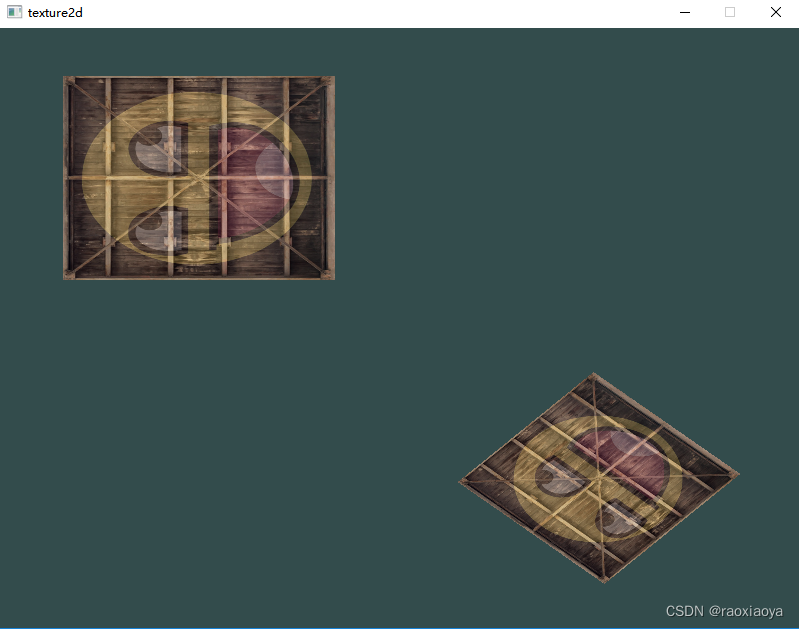
坐标系统

一个顶点在最终被转化为片段之前需要经历的所有不同状态。

• 局部空间(Local Space)，或者称为物体空间(Object Space)
• 世界空间(World Space)
• 观察空间(View Space)，或者称为视觉空间(Eye Space)，摄像机空间(Camera Space)
• 裁剪空间(Clip Space)
• 屏幕空间(Screen Space)

为了将坐标从一个坐标系变换到另一个坐标系，我们需要用到几个变换矩阵，最重要的几个分别是模型(Model)、观察(View)、投影(Projection)三个矩阵。我们的顶点坐标起始于局部空间(Local Space)，在这里它称为局部坐标(Local Coordinate)，它在之后会变为世界坐标(World Coordinate)，观察坐标(View Coordinate)，裁剪坐标(Clip Coordinate)，并最后以屏幕坐标(Screen Coordinate)的形式结束。下面的这张图展示了整个流程以及各个变换过程做了什么：

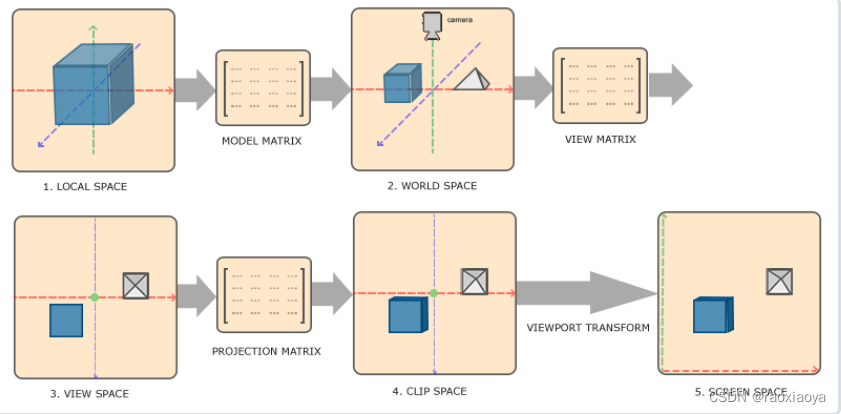
矩阵变换

• 从局部空间变换到世界空间：模型矩阵(Model Matrix)。
• 从世界空间变换到观察空间：观察矩阵(View Matrix)。
• 从观察空间变换到裁剪空间：投影矩阵(Projection Matrix)。

一旦所有顶点被变换到裁剪空间，最终的操作——透视除法(Perspective Division)将会执行，在这个过程中我们将位置向量的x，y，z分量分别除以向量的齐次w分量；透视除法是将4D裁剪空间坐标变换为3D标准化设备坐标的过程。这一步会在每一个顶点着色器运行的最后被自动执行。

将观察坐标变换为裁剪坐标的投影矩阵可以为两种不同的形式，每种形式都定义了不同的平截头体。我们可以选择创建一个正射投影矩阵(Orthographic Projection Matrix)或一个透视投影矩阵(Perspective Projection Matrix)。

正射投影

它由宽、高、近(Near)平面和远(Far)平面所指定。

// near平面为靠近观察者的平面
// 参数一二，表示near平面的左右坐标
// 参数三四，表示near平面的底顶坐标
// 参数五六，near和far平面距离屏幕的距离
mgl32.Ortho(0, 800, 0, 600, 0.1, 100)

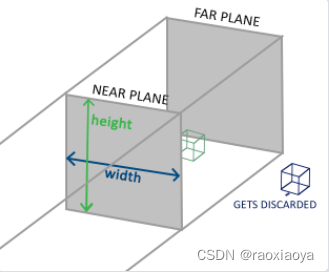
正射投影对近处和远处的物体都一视同仁，也就说每个顶点的w分量都是1，但这与现实不符，实际上，同样大小的物体，距离人眼越远会看到的越小，这是由眼睛的构造决定的。

透视投影

// 第一个参数为视野角，通常为45度。
// 第二个参数为视口的宽高比。
// near和far平面距离屏幕的距离。通常设置near为0.1，far为100
mgl32.Perspective(mgl32.DegToRad(45.0), float32(windowWidth)/windowHeight, 0.1, 10.0)

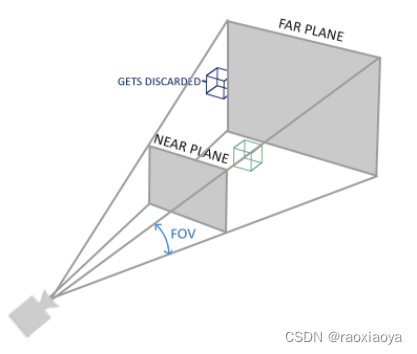
距离摄像机越远，能看到的视野越大，但是屏幕大小是固定的，于是物体是会缩小的。

会修改w分量，离观察者越远的顶点坐标w分量越大。最后会让x,y,z都除以w分量，于是远处的物体就变小了。

视野角的特性：角度越小，那么看到的场景范围就越小，投影到屏幕上反而是放大的效果；反之，视野角越大，是缩小的效果。

最后的变换过程：

V_clip = M_projection * M_view * M_model * V_local

具体实践

Model Matrix

我们在一个房间里面（世界空间）画了两个桌子，它们分别在世界坐标系原点的左边和右边，当我们进入左边桌子进行绘制的时候，为了绘制方便我们会将坐标原点放在桌子的中心，此时就是局部空间了，画完了之后我们需要返回到世界空间来看整体效果，我们需要先将桌子变小（因为在画的时候我会让它占了屏幕的大部分），变小之后我们就能看到整个场景了，但是刚才画的那个桌子的中心是在世界空间的中心上的，我们需要将其挪一下，如果桌子应该是斜着摆放的，那么还需要先旋转一下，也就是说 Model 是用来调整单个的物体，你会发现，平移，缩放，旋转三个操作应该是由顺序的。应该是缩放 --> 旋转 --> 平移。

View Matrix

来到了世界空间之后，我们该从哪个角度来观察这个空间呢，换句话说，做为图形工具，应该将哪个角度的景象呈现给用户呢，这里就有一个摄像机的概念，可以理解为用户的眼睛，将摄像机向后移动，和将整个场景向前移动是一样的，也就是说 View 是用来调整整个场景的。OpenGL是一个右手坐标系，所以我们需要沿着z轴的正方向移动。我们会通过将场景沿着z轴负方向平移来实现。它会给我们一种我们在往后移动的感觉。想象一下，一个立体的场景在那里不动，人可以选择从不同的点位来观察它，摄像机不能旋转，它永远是垂直于屏幕在看。当然，我们也可以让摄像机转到起来，这是另外一个知识点。

Projection Matrix

将场景投影到窗口区域上，它决定了要将哪部分场景投影到屏幕上。

model := mgl32.HomogRotate3D(mgl32.DegToRad(-55), mgl32.Vec3{1, 0, 0})
view := mgl32.Translate3D(0, 0, -3)
projection := mgl32.Perspective(mgl32.DegToRad(45), float32(width)/float32(height), 0.1, 100)
transe := projection.Mul4(view).Mul4(model)
gl.UniformMatrix4fv(gl.GetUniformLocation(program, gl.Str("transe\x00")), 1, false, &transe[0])

如果有3D效果，那么就需要开启深度测试，它会对遮挡进行处理，否则效果比较奇怪。

gl.Enable(gl.DEPTH_TEST)

gl.Clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT)

---

摄像机

前面将的坐标系统，是假设摄像机不动，而是场景在动，物体在动，其实还有一种观察方式就是让摄像机也动起来。

定义一个摄像机，就是创建一个三个单位轴相互垂直的、以摄像机的位置为原点的坐标系。

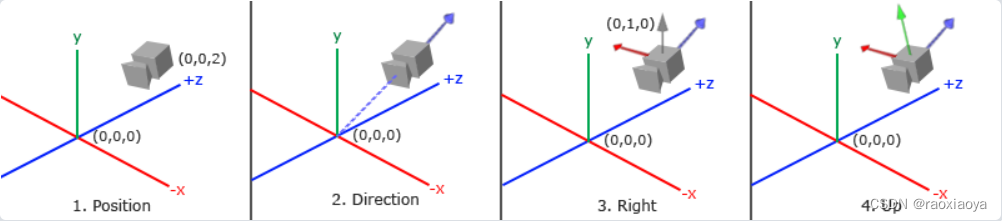
定义一个摄像机的步骤：

• 摄像机的位置：世界空间中的一个点，代表摄像机放在这里，位置越远看到的物体越小，P1(x,y,z)。

  cameraPos := mgl32.Vec3{0, 0, 3}
  

• 摄像机的方向：在世界空间中，摄像机指向哪里，因为它代表的只是一个方向，因此在该方向上选取一点即可，比如摄像机指向原点P2(0,0,0)，那么摄像机的方向就是 P1-P2，就是图中蓝色的箭头，但是这个方向却和摄像机拍照的方向相反。

  cameraTarget := mgl32.Vec3{0, 0, 0}
  cameraDirction := cameraPos.Sub(cameraTarget)
  

• 右轴：也叫X轴正方形，为获取右向量我们需要先使用一个小技巧：先定义一个上向量(Up Vector)。接下来把上向量和第二步得到的方向向量进行叉乘。两个向量叉乘的结果会同时垂直于两向量，因此我们会得到指向x轴正方向的那个向量（如果我们交换两个向量叉乘的顺序就会得到相反的指向x轴负方向的向量）。

  up := mgl32.Vec3{0, 1, 0}
  cameraRight := up.Cross(cameraDirction)
  

• 上轴：现在我们已经有了x轴向量和z轴向量，获取一个指向摄像机的正y轴向量就相对简单了：我们把右向量和方向向量进行叉乘。

  cameraUp := cameraDirction.Cross(cameraRight)
  

于是我们发现，只要给定了cameraPos, cameraTarget, up三个向量，我们就可以构造出一个摄像机坐标，于是就有了LookAt函数。

camera := mgl32.LookAtV(cameraPos, cameraTarget, up)

在使用的过程中，摄像机其实就是view，因此顺序是projection * camera * model。

示例1

一个立方体绕着Y轴旋转，正常情况下我们只能看到Y轴这个面，加入了相机之后我们就能看到一个立体效果。

model := mgl32.HomogRotate3D(float32(glfw.GetTime()), mgl32.Vec3{0, 1, 0})
camera := mgl32.LookAtV(mgl32.Vec3{2, 2, 2}, mgl32.Vec3{0, 0, 0}, mgl32.Vec3{0, 1, 0})
projection := mgl32.Perspective(mgl32.DegToRad(45), float32(width)/height, 0.1, 100)
transe := projection.Mul4(camera).Mul4(model)
gl.UniformMatrix4fv(gl.GetUniformLocation(program, gl.Str("transe\x00")), 1, false, &transe[0])

示例2

场景不动，摄像机的位置围绕着一个圆旋转，圆半径为3

radius := 3.0
cx := float32(math.Sin(glfw.GetTime()) * radius)
cz := float32(math.Cos(glfw.GetTime()) * radius)
camera := mgl32.LookAtV(mgl32.Vec3{cx, 2, cz}, mgl32.Vec3{0, 0, 0}, mgl32.Vec3{0, 1, 0})
projection := mgl32.Perspective(mgl32.DegToRad(45), float32(width)/height, 0.1, 100)
transe := projection.Mul4(camera)
gl.UniformMatrix4fv(gl.GetUniformLocation(program, gl.Str("transe\x00")), 1, false, &transe[0])

示例3

使用按键WSAD来控制相机左右前后移动，

cameraPos := mgl32.Vec3{0, 0, 3}
cameraFront := mgl32.Vec3{0, 0, -1}
cameraUp := mgl32.Vec3{0, 1, 0}

func KeyPressAction(window *glfw.Window) {
	keyCallback := func(w *glfw.Window, key glfw.Key, scancode int, action glfw.Action, mods glfw.ModifierKey) {
		cameraSpeed := float32(0.05)
		if key == glfw.KeyW && action == glfw.Press {
			cameraPos = cameraPos.Sub(cameraFront.Mul(cameraSpeed))
		}
		if key == glfw.KeyS && action == glfw.Press {
			cameraPos = cameraPos.Add(cameraFront.Mul(cameraSpeed))
		}
		if key == glfw.KeyA && action == glfw.Press {
             // Normalize 标准化坐标使其落在 [-1,1]
			cameraPos = cameraPos.Add(cameraFront.Cross(cameraUp).Normalize().Mul(cameraSpeed))
		}
		if key == glfw.KeyD && action == glfw.Press {
			cameraPos = cameraPos.Sub(cameraFront.Cross(cameraUp).Normalize().Mul(cameraSpeed))
		}
         // log.Println(cameraPos, cameraPos.Add(cameraFront))
	}
	window.SetKeyCallback(keyCallback)
}

func Run10() {
	......
	KeyPressAction(window)

	for !window.ShouldClose() {
		......
         // 这样能保证无论我们怎么移动，摄像机都会注视着目标方向
		camera := mgl32.LookAtV(cameraPos, cameraPos.Add(cameraFront), cameraUp)
		projection := mgl32.Perspective(mgl32.DegToRad(45), float32(width)/height, 0.1, 100)
		transe := projection.Mul4(camera)
		gl.UniformMatrix4fv(gl.GetUniformLocation(program, gl.Str("transe\x00")), 1, false, &transe[0])

		......

		glfw.PollEvents()
		window.SwapBuffers()
	}
}

A和D需要正交移动，因此要用向量的叉乘。

上面注释中有些这样能保证无论我们怎么移动，摄像机都会注视着目标方向，该如何理解呢，我们在keyCallback中增加打印来细细观察，因为WSAD操作只改变了cameraPos值，而cameraFront只有Z方向，因此cameraTarget = cameraPos + cameraFront会导致摄像机的朝向始终平行于Z轴，跟最开始的时候一样。

---

视角移动

欧拉角

欧拉角(Euler Angle)是可以表示3D空间中任何旋转的3个值，由莱昂哈德·欧拉(Leonhard Euler)在18世纪提出。一共有3种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)，下面的图片展示了它们的含义：

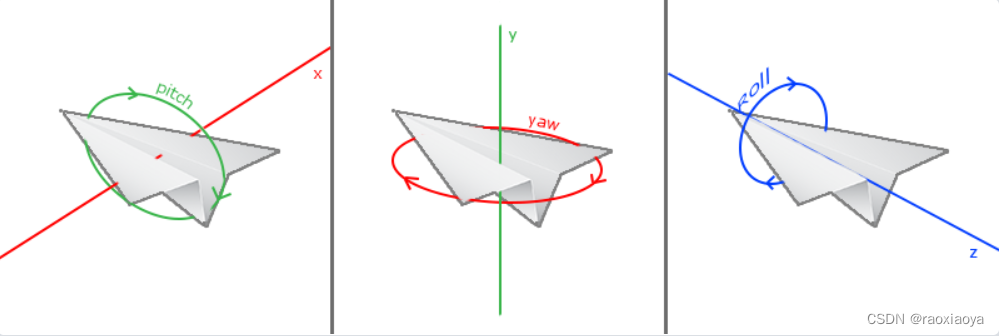
俯仰角是描述我们如何往上或往下看的角，可以在第一张图中看到。第二张图展示了偏航角，偏航角表示我们往左和往右看的程度。滚转角代表我们如何翻滚摄像机，通常在太空飞船的摄像机中使用。每个欧拉角都有一个值来表示，把三个角结合起来我们就能够计算3D空间中任何的旋转向量了。

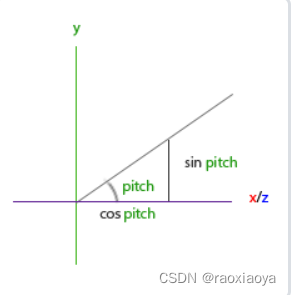
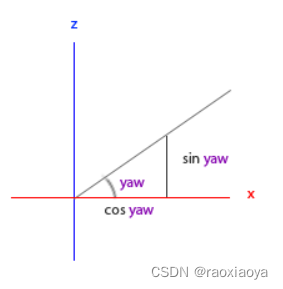
最终的方向向量计算公式

// direction代表摄像机的前轴(Front)，这个前轴是和本文第一幅图片的第二个摄像机的方向向量是相反的
direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw)); 
direction.y = sin(glm::radians(pitch));
direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));

鼠标控制

鼠标坐标系的原点为屏幕左上角，向右为X正，向下为Y正，因此Y轴的增量应该反过来。

刚进来的时候会出现抖动，那是因为默认的cursorX，cursorY在屏幕中心，而鼠标刚开始并不在屏幕中心，因此要初始化起始点。

俯仰角，要让用户不能看向高于89度的地方（在90度时视角会发生翻转），同样也不允许小于-89度。这样能够保证用户只能看到天空或脚下，但是不能超越这个限制。类比于人的眼睛仰视和俯视，超过了90度看到的东西会反过来。

偏航角却可以是360度旋转。

如果把yaw和pitch的初始值设置为0，你会发现一进来动一下鼠标就变成了空白，那是因为我们的相机朝向出了问题，而相机的朝向就是cameraFront决定的，那么初始值怎么设置呢，cameraFront的初始值为(0,0,-1)，鼠标进到屏幕后应该是线性变化的，不能是突变，所以yaw和pitch的初始值就是使cameraFront = (0,0,-1)，我们来分析它的公式就知道pitch = 0, yaw = -90。

var firstMouse bool
var cursorX float64 = 400
var cursorY float64 = 300
var yaw float64 = -90
var pitch float64
sensitivity := 0.05 // 鼠标移动的灵敏度
cursorPosCallback := func(w *glfw.Window, xpos float64, ypos float64) {
    if firstMouse {
        cursorX = xpos
        cursorY = ypos
        firstMouse = false
    }

    xoffset := sensitivity * (xpos - cursorX)
    yoffset := sensitivity * (cursorY - ypos)
    cursorX = xpos
    cursorY = ypos
    yaw += xoffset
    pitch += yoffset
    if pitch > 89 {
        pitch = 89
    }
    if pitch < -89 {
        pitch = -89
    }

    cameraFront = mgl32.Vec3{
        float32(math.Cos(float64(mgl32.DegToRad(float32(pitch)))) * math.Cos(float64(mgl32.DegToRad(float32(yaw))))),
        float32(math.Sin(float64(mgl32.DegToRad(float32(pitch))))),
        float32(math.Cos(float64(mgl32.DegToRad(float32(pitch)))) * math.Sin(float64(mgl32.DegToRad(float32(yaw))))),
    }.Normalize()
}
window.SetCursorPosCallback(cursorPosCallback)

天空盒
前面我们讲过，纹理贴图默认是双面贴的，也就是说立方体内部也贴好了，但是细细分析就会发现，外面和里面的图片是左右翻转的，如果此时我们把相机位置放到立方体中心会怎么样呢，其实这就是一个天空盒的效果，通过控制鼠标，我们可以在一个内部空间遨游。当然，更精细的天空盒需要六个面有不同的贴图。

当然，天空盒的正确操作应该是使用立方体贴图，也就是纹理坐标是三维的，参考实现 https://learnopengl-cn.github.io/04%20Advanced%20OpenGL/06%20Cubemaps

首先是创建立方体纹理

func MakeTextureCube(filepathArray []string) uint32 {
	var texture uint32
	gl.GenTextures(1, &texture)
	gl.BindTexture(gl.TEXTURE_CUBE_MAP, texture)

	for i := 0; i < len(filepathArray); i++ {
		imgFile2, _ := os.Open(filepathArray[i])
		defer imgFile2.Close()
		img2, _, _ := image.Decode(imgFile2)
		rgba2 := image.NewRGBA(img2.Bounds())
		draw.Draw(rgba2, rgba2.Bounds(), img2, image.Point{0, 0}, draw.Src)

		// right, left, top, bottom, back, front
		//
		// TEXTURE_CUBE_MAP_POSITIVE_X   = 0x8515
		// TEXTURE_CUBE_MAP_NEGATIVE_X   = 0x8516
		// TEXTURE_CUBE_MAP_POSITIVE_Y   = 0x8517
		// TEXTURE_CUBE_MAP_NEGATIVE_Y   = 0x8518
		// TEXTURE_CUBE_MAP_POSITIVE_Z   = 0x8519
		// TEXTURE_CUBE_MAP_NEGATIVE_Z   = 0x851A
		gl.TexImage2D(gl.TEXTURE_CUBE_MAP_POSITIVE_X+uint32(i), 0, gl.RGBA, int32(rgba2.Rect.Size().X), int32(rgba2.Rect.Size().Y), 0, gl.RGBA, gl.UNSIGNED_BYTE, gl.Ptr(rgba2.Pix))
	}

	gl.TexParameteri(gl.TEXTURE_CUBE_MAP, gl.TEXTURE_WRAP_S, gl.CLAMP_TO_EDGE)
	gl.TexParameteri(gl.TEXTURE_CUBE_MAP, gl.TEXTURE_WRAP_T, gl.CLAMP_TO_EDGE)
	gl.TexParameteri(gl.TEXTURE_CUBE_MAP, gl.TEXTURE_WRAP_R, gl.CLAMP_TO_EDGE)
	gl.TexParameteri(gl.TEXTURE_CUBE_MAP, gl.TEXTURE_MIN_FILTER, gl.LINEAR)
	gl.TexParameteri(gl.TEXTURE_CUBE_MAP, gl.TEXTURE_MAG_FILTER, gl.LINEAR)

	return texture
}

然后是顶点数据，我们不需要设置纹理坐标，而是直接取的顶点坐标作为纹理坐标。

#version 410

in vec3 vPosition;
out vec3 textureDir;

uniform mat4 transe;

void main() {
	gl_Position = transe * vec4(vPosition, 1.0);
	textureDir = vPosition;
}

在片元着色器中使用samplerCube

#version 410

in vec3 textureDir;

out vec4 frag_colour;

uniform samplerCube cubemap;

void main() {
	frag_colour = texture(cubemap, textureDir);
}

在传入图片的时候也是按照顺序right, left, top, bottom, back, front。

滚轮控制缩放

视野(Field of View)或fov定义了我们可以看到场景中多大的范围。当视野变小时，场景投影出来的空间就会减小，产生放大(Zoom In)了的感觉。我们会使用鼠标的滚轮来放大。与鼠标移动、键盘输入一样，我们需要一个鼠标滚轮的回调函数，当滚动鼠标滚轮的时候，yoff 值代表我们竖直滚动的大小。当scrollCallback函数被调用后，我们改变全局变量fov变量的内容。因为45.0f是默认的视野值，我们将会把缩放级别(Zoom Level)限制在1.0f到45.0f。

var fov float64 = 45
scrollCallback := func(w *glfw.Window, xoff float64, yoff float64) {
    if fov >= 1.0 && fov <= 45.0 {
        fov -= yoff
    }
    if fov <= 1.0 {
        fov = 1.0
    }
    if fov >= 45.0 {
        fov = 45.0
    }
}
window.SetScrollCallback(scrollCallback)
......
projection := mgl32.Perspective(mgl32.DegToRad(float32(fov)), float32(width)/height, 0.1, 100)

---

保存图片

我们可以将当前窗口中的图形保存为图片，比如设置键盘事件ctrl+s就保存一次。
可以使用gl.ReadPixels()函数，我们知道glfw使用的是双缓冲区，该函数会读取前缓冲区的数据。
func ReadPixels(x int32, y int32, width int32, height int32, format uint32, xtype uint32, pixels unsafe.Pointer)

x和y表示起始点坐标，窗口的左下角为(0,0)，向上Y正，向右X正；然后就是要截取的宽高，最后三个参数跟gl.TexImage2D()函数是一样的。

但是我们用的图形库基本都是将左上角作为(0,0)点的，因此保存的图片是Y轴上下颠倒的，因此需要自行翻转Y轴。

func (c *Camera) SavePng(filepath string) {
	img := image.NewRGBA(image.Rect(0, 0, c.WindowWidth, c.WindowHeight))

	gl.ReadPixels(0, 0, int32(c.WindowWidth), int32(c.WindowHeight), gl.RGBA, gl.UNSIGNED_BYTE, gl.Ptr(img.Pix))

	// 翻转Y坐标
	for x := 0; x < c.WindowWidth; x++ {
		for y := 0; y < c.WindowHeight/2; y++ {
			s := img.RGBAAt(x, y)
			t := img.RGBAAt(x, c.WindowHeight-1-y)
			img.SetRGBA(x, y, t)
			img.SetRGBA(x, c.WindowHeight-1-y, s)
		}
	}

	if filepath == "" {
		filepath = strconv.Itoa(int(time.Now().Unix())) + ".png"
	}
	f, _ := os.Create(filepath)
	b := bufio.NewWriter(f)
	png.Encode(b, img)
	b.Flush()
	f.Close()
}