目录
二次型
概念
示例
性质和特点
特征值与特征向量
概念
示例
注意
性质和特点
特征值分解
注意
多元函数的泰勒展开
回顾一元函数泰勒展开
多元函数的泰勒展开
二次型
概念
二次型是一个关于向量的二次多项式,通常用矩阵表示。
考虑一个n维向量x = [x₁, x₂, ..., xn],对应的二次型可以表示为:
Q(x) = xᵀA𝑥
其中,xᵀ表示向量x的转置,A是一个n×n的实对称矩阵。
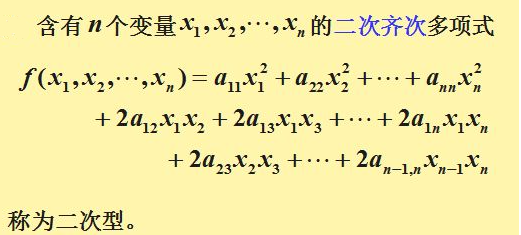
示例
二次型可以使用向量与矩阵相乘的形式表示

为了研究方便,二次型使用x^T^Ax的形式表示,其中,中间的矩阵A为对称矩阵
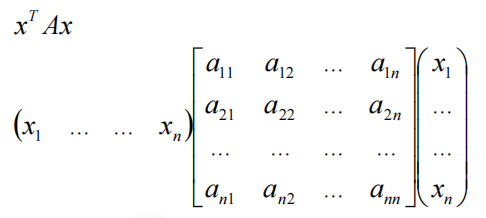
性质和特点
-
对称性:如果系数矩阵A是对称矩阵,即Aᵀ = A,那么二次型Q(x)是对称的,即Q(x) = Q(xᵀ)。
-
标准形式:通过合适的线性变换,可以将任何二次型转化为标准形式。标准形式是指二次型只包含平方项,而没有交叉项和常数项。通过正交变换可以实现这样的转化。
-
矩阵特征值:二次型的矩阵A的特征值与二次型的正负定性相关。如果A的所有特征值都大于零,则二次型是正定的;如果所有特征值都小于零,则二次型是负定的;如果特征值既有正又有负,则二次型是不定的。
-
几何意义:二次型在几何上表示为一个二次曲面或椭圆抛物面。二次型的正负定性与曲面的凸凹性和极值点的性质相关。
-
应用:二次型在优化问题、矩阵理论、统计学、物理学等领域中有广泛的应用。它们在最小二乘问题、二次规划、协方差矩阵分析、精确度矩阵等方面发挥重要作用。
特征值与特征向量
概念
设A是n阶方阵,如果数λ和n维非零向量x使关系式Ax = λx成立,那么,λ称为方阵A
的特征值;非零向量x称为A的属于特征值λ的特征向量。
示例
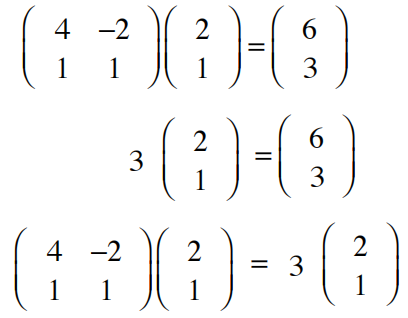
则数3为方阵[4 -2,1 1]的特征值;非零向量(2,1)为方阵[4 -2,1 1]的属于特征值3的特征向量。
注意
- 特征值与特征向量是针对方阵而言的
- 特征向量是非零向量
- 同一个特征值λ对应无穷多个特征向量
性质和特点
-
特征向量:特征向量v是与特征值λ关联的非零向量。它表示在矩阵A的作用下,保持在该方向上只发生伸缩变化而不改变方向。
-
特征值:特征值λ是与特征向量v关联的标量。它表示特征向量v在矩阵A的作用下发生的伸缩比例。特征值可以是实数或复数。
-
特征空间:特征空间是由所有与特定特征值关联的特征向量所张成的向量空间。对于特定特征值λ,特征空间包含所有满足A·v = λ·v的特征向量v。
-
特征分解:特征分解是将一个矩阵分解为特征向量和特征值的形式。对于一个可对角化的矩阵,可以表示为 A = P·D·P⁻¹,其中P是由特征向量组成的矩阵,D是对角矩阵,其对角线上的元素是矩阵A的特征值。
-
特征值与矩阵性质:特征值与矩阵的很多性质和行为密切相关。例如,特征值的个数等于矩阵的秩;矩阵的特征值之和等于其主对角线上元素之和(迹);特征值的乘积等于矩阵的行列式。
特征值分解
特征值分解是将一个矩阵分解成下面的形式:
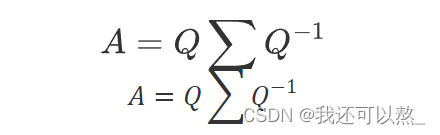
其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角矩阵(只有对角线上有非0元
素的矩阵称为对角矩阵),对角线的值是由矩阵所有特征值构成的。
其中,Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角矩阵,每一个对角线元素
就是一个特征值,里面的特征值是由大到小排列的,这些特征值所对应的特征向量就是描述
这个矩阵变化方向(从主要的变化到次要的变化排列)。也就是说矩阵A的信息可以由其特
征值和特征向量表示。
对于矩阵为高维的情况下,那么这个矩阵就是高维空间下的一个线性变换。可以想象,
这个变换也同样有很多的变换方向,我们通过特征值分解得到的前N个特征向量,那么就对
应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向,就可以近似这个矩阵
(变换)。
注意
- 特征值分解可以得到特征值与特征向量
- 特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么
- 特征值分解是针对于方阵而言
多元函数的泰勒展开
回顾一元函数泰勒展开
函数 f(x)在含 x~k~ 的某个开区间 (a,b)内具有直到 n 阶导数,则对任意的 x∈(a,b)有
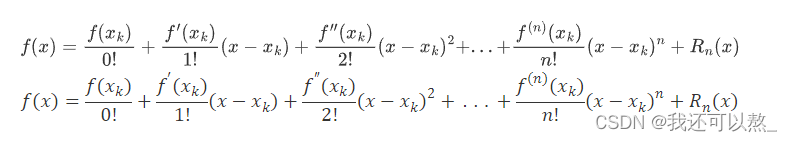
其中,x~0~是泰勒公式的展开点,R~n~(x)是泰勒公式的余项。
展开二项的形式为:
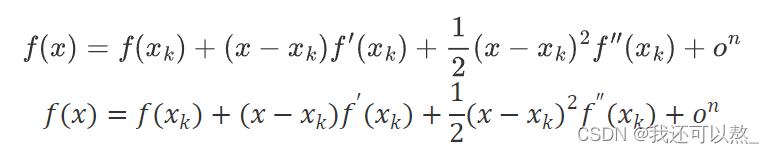
多元函数的泰勒展开
f(x~k~)是标量,而且是个常数;不过注意(x-x~k~)是个向量,然后T转置这里是把梯度和
(x-x~k~)做内积;二次项的内积,是和 hessian 矩阵做内积。
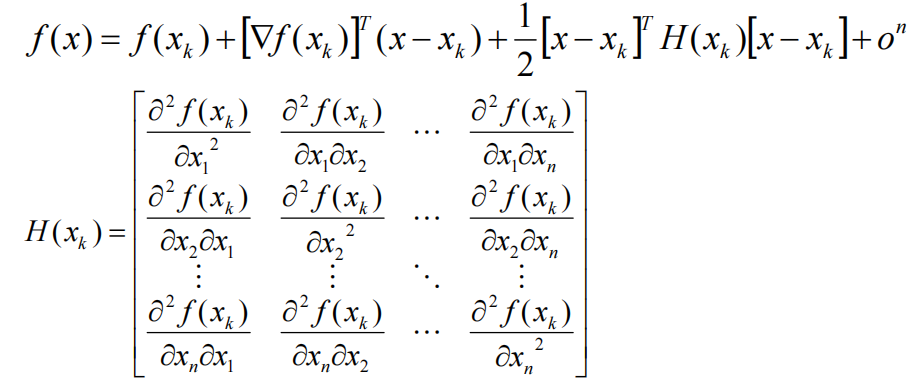
多元函数泰勒展开是非常有用的,例如在推导梯度下降法,牛顿法的时候会用的到的。