1. 归并排序 递归

1.基本思想

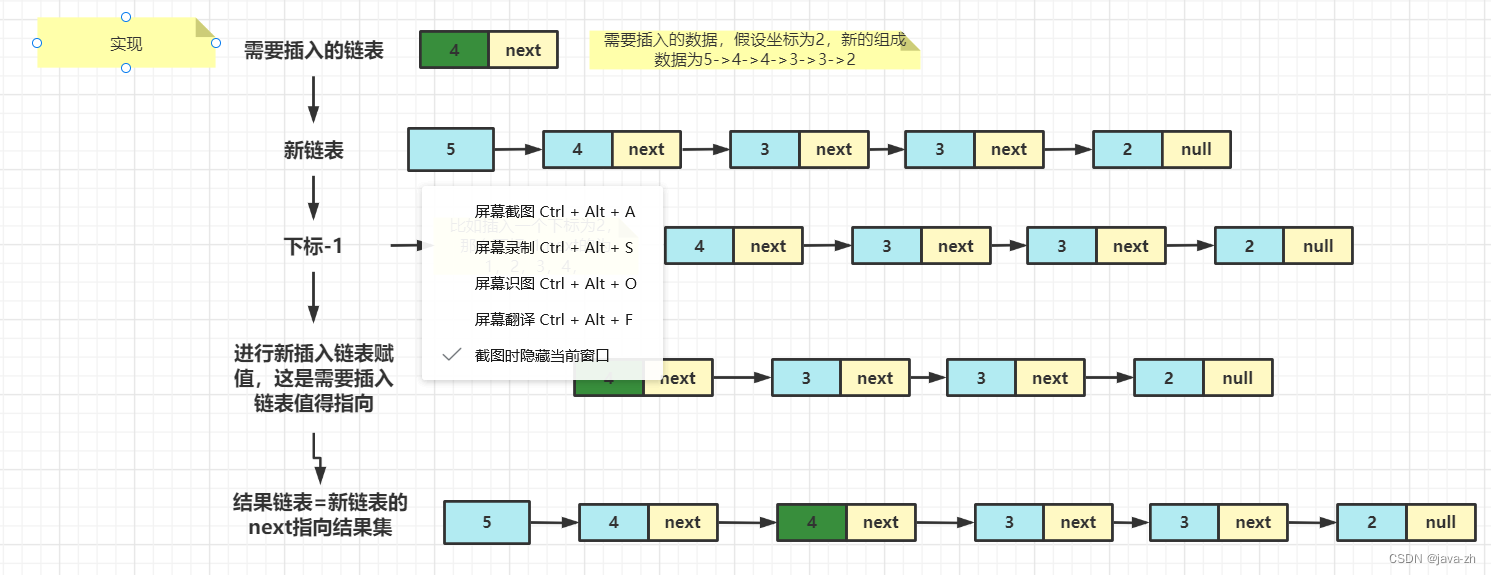
主要使用了 分治思想 即 大事化小 ，先使每个子序列有序，子使序列段有序，将两个有序表合并成一个有序表

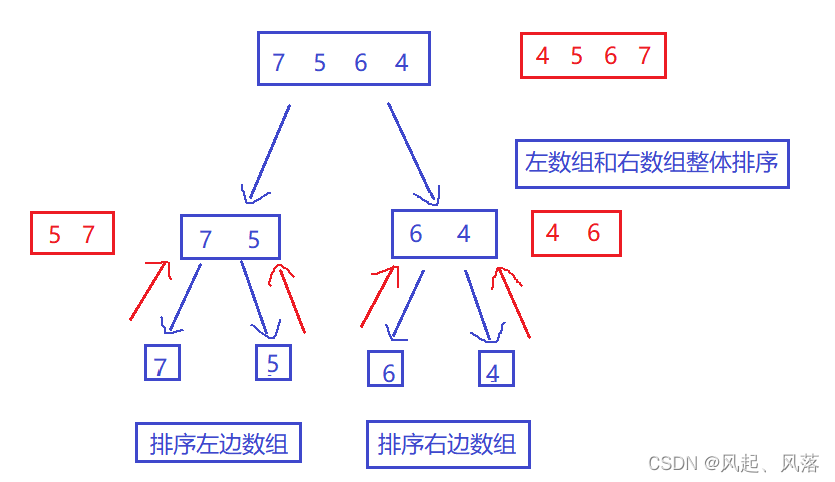
2. 使用两个函数完成归并

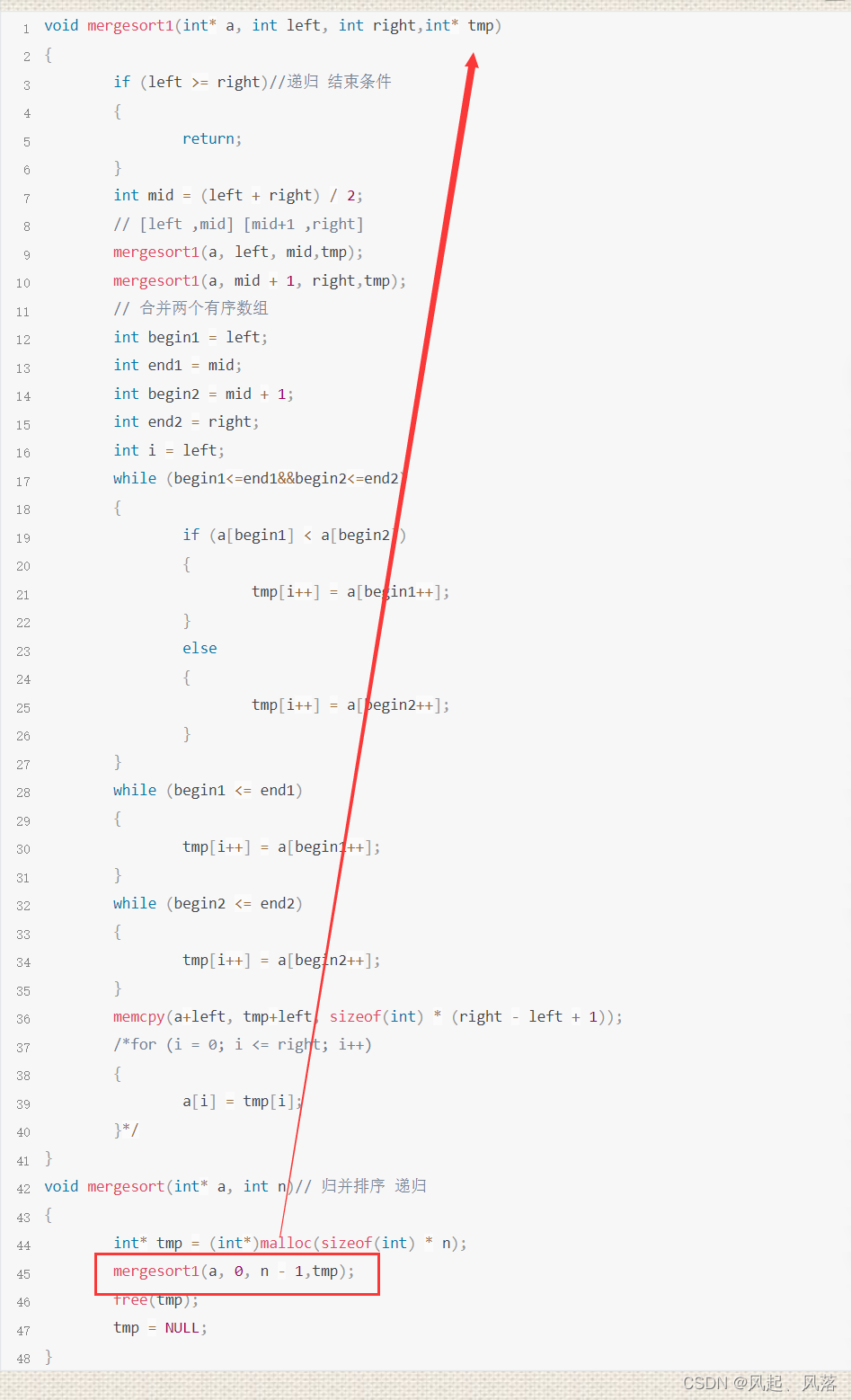
因为想要malloc只开辟一块空间，而不是设置在mergesort1函数中每递归一次开辟一块空间,极大节省开辟空间开销

3. 递归结束条件

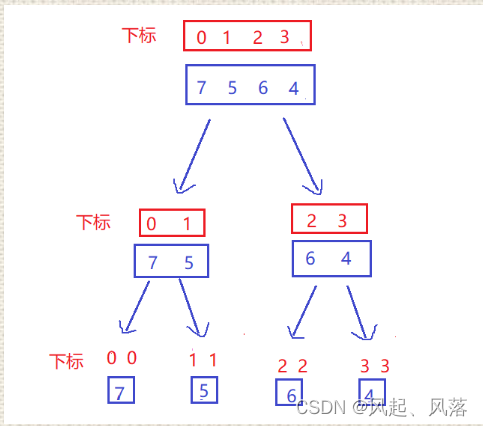
当下标 left 与right 相等时，正好为一个数，即 return 返回

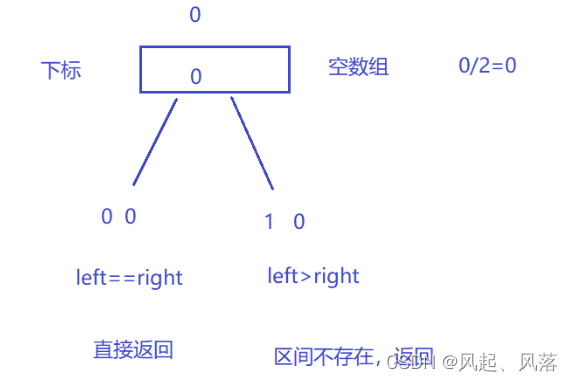
当数组为0，就会发生 left>right，区间不存在

4.时间复杂度与空间复杂度计算

1. 时间复杂度

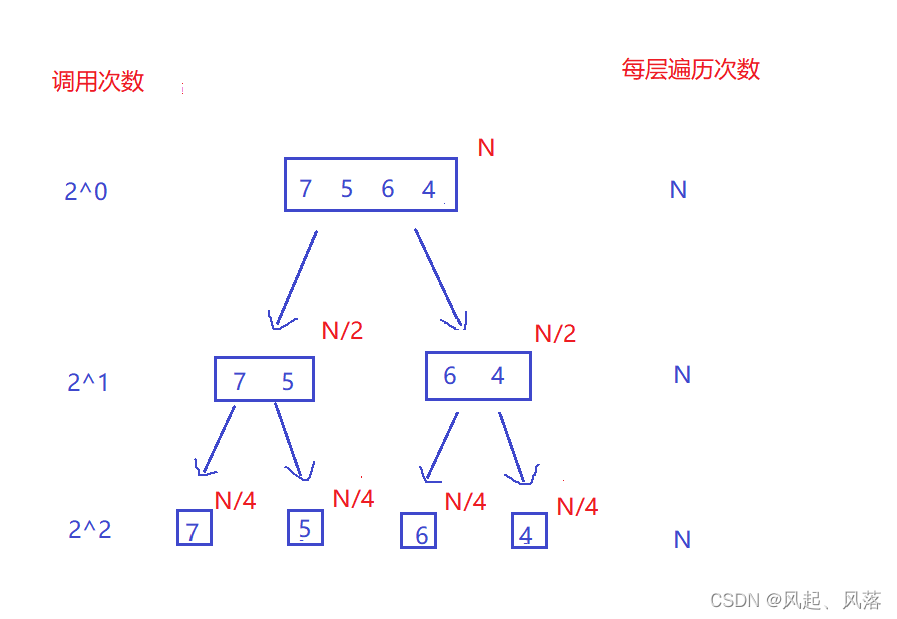
归并整个过程，类似一颗满二叉树，
调用次数：2^h-1=N h=logN
每一层遍历次数 ：N
整体时间复杂度为 O(N*logN)

2. 空间复杂度

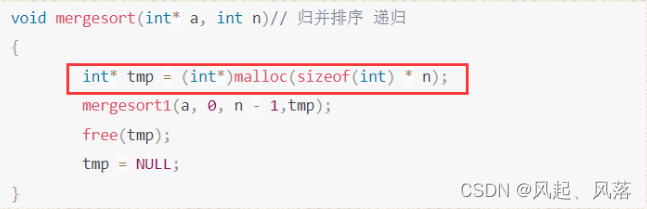
刚开始 开辟了 一个大小为n的 临时数组 tmp
空间复杂度为 O(N)

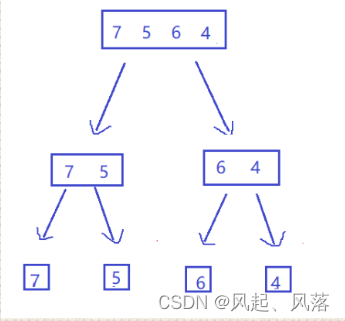
正常来说，我们递归也会产生函数栈帧，调用次数 —— 空间复杂度即O(logN)

整体空间复杂度为 O(N+logN)
但是由于大o的渐进表示法 即 O(N)

5. 代码

void mergesort1(int* a, int left, int right,int* tmp)
{
if (left >= right)//递归 结束条件
{
return;
}
int mid = (left + right) / 2;
// [left ,mid] [mid+1 ,right] 
mergesort1(a, left, mid,tmp);
mergesort1(a, mid + 1, right,tmp);
// 合并两个有序数组，并将其赋给临时数组tmp，最后拷贝原数组中(合并一部分，拷贝一部分)
int begin1 = left;
int end1 = mid;
int begin2 = mid + 1;
int end2 = right;
int i = left;//由于部分合并，所以i从left开始
while (begin1<=end1&&begin2<=end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
 //若出了循环后，也有可能在两个数组有剩余的情况
while (begin1 <= end1)//若 [begin1,end1]数组有剩余，直接赋值到tmp数组
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)//若 [begin2,end2]数组有剩余，直接赋值到tmp数组
{
tmp[i++] = a[begin2++];
}
 //第一种拷贝方式
memcpy(a+left, tmp+left, sizeof(int) * (right - left + 1));
 //第二种拷贝方式
/*for (i = 0; i <= right; i++)
{
a[i] = tmp[i];
}*/
}
void mergesort(int* a, int n)// 归并排序 递归
{
int* tmp = (int*)malloc(sizeof(int) * n);
mergesort1(a, 0, n - 1,tmp);
free(tmp);
tmp = NULL;
}

2. 归并排序 非递归

1. 思想

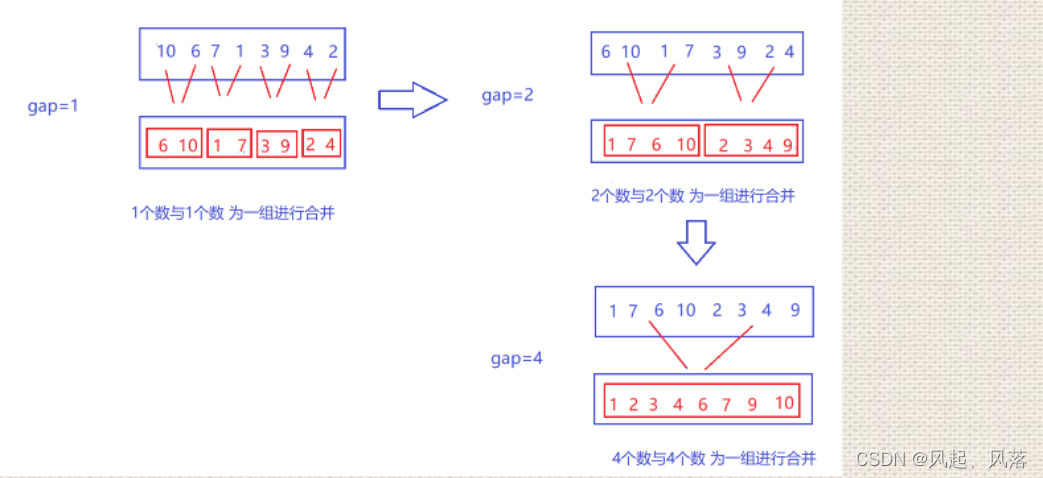
将一个数组 ，通过gap分为几组进行合并，gap每次扩大2倍,gap<n
合并方式与递归相同
第一个数组的 begin1 改为 i
第一个数组的 end1 改为 i+gap-1
第二个数组 的 begin2改为 i+gap
第二个数组的 end2 改为 i+2*gap-1

2. 越界问题

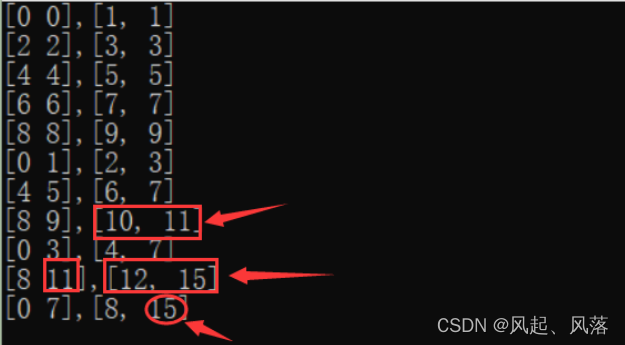
int a[] = { 6,1,2,7,9,3,4,5,6,8 };
共有10个数，下标到9
1.end1 beign2 end2 越界
2.begin2 end2 越界
3.end2 越界

1. .end1 beign2 end2 越界

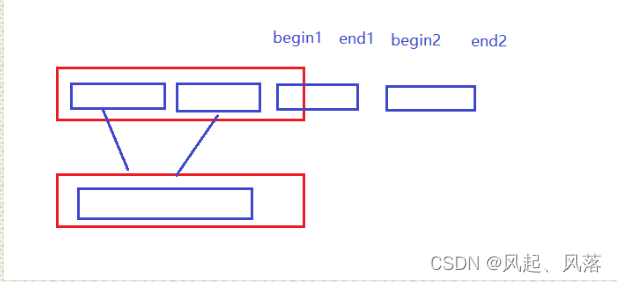
方式 1

直接break
因为右边没有数据存在，所以就算是进入循环中剩余区间中的数也不会发生改变

方式 2

修正区间
因为begin2 与end2区间不存在，
end1=n-1 end1设置成边界
设置一个不存在的区间
begin2 =n
end2= n-1
begin2>end2 不进入循环 合并，直接拷贝回剩余的区间

整体拷贝与拷贝一部分，归并一部分的区别

以上一个的end1 begin2 end2 越界为例
同样使用break
拷贝一部分，归并一部分就能存在剩余的区间

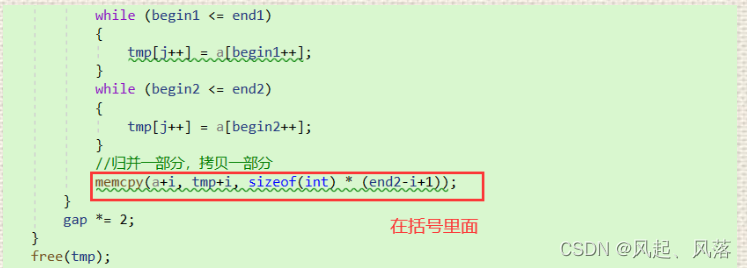
整体拷贝就会丢掉剩余的区间

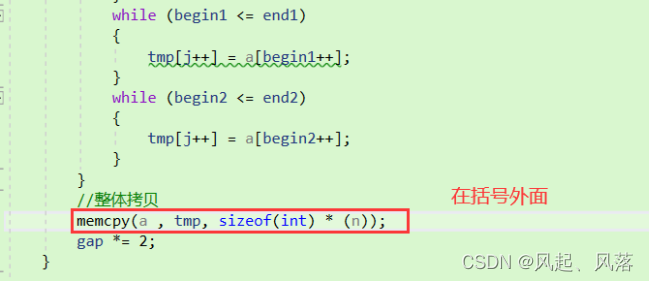
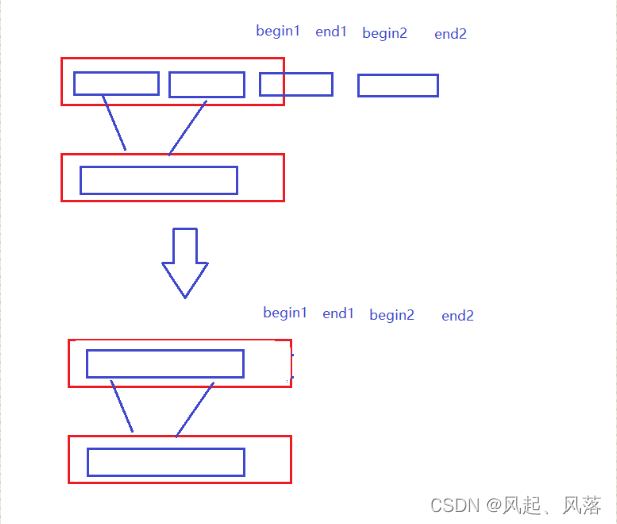
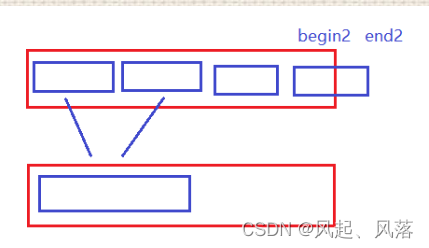
2. begin2 end2 越界

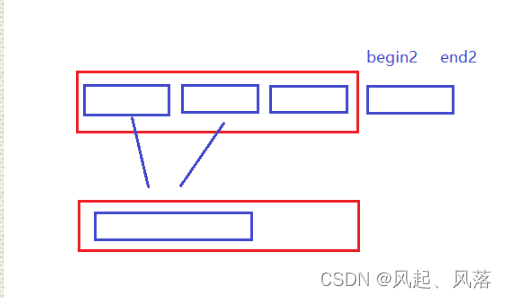
方式 1

直接break
因为右边没有数据存在，所以就算是进入循环中剩余区间中的数也不会发生改变

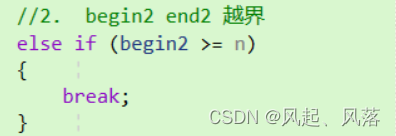
方式 2

修正区间
设置一个不存在的区间
begin2 =n
end2= n-1
begin2>end2 不进入循环 合并，直接拷贝回剩余的区间

3. end2 越界

修正end2区间
end2=n-1 ，而n-1正好为边界

3. 代码

void mergesortNonR(int* a, int n)//归并排序 非递归
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	int gap = 1;
	int i = 0;
	int j = 0;
	while (gap < n)
	{
		for (i = 0; i < n; i += 2*gap)
		{
			//[ i , i+gap-1][i+gap,i+2*gap-1]
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + 2*gap-1 ;
			j = i;

			//1. end1 begin2 end2 越界
			if (end1 >= n)//end2是下标的存在 ，最多取到 n-1
			{
				break;
			}
			//if (end1 >= n)//修正区间
			//{
			//	end1 = n - 1;
			//	begin2 = n;
			//	end2 = n - 1;
			//}
			//2.  begin2 end2 越界
			else if (begin2 >= n)
			{
				break;
			}
			/*else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}*/
			//3. end2 越界
			else if (end2 >= n)
			{
				end2 = n - 1;
			}
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			//归并一部分，拷贝一部分
			memcpy(a+i, tmp+i, sizeof(int) * (end2-i+1));
		}
		gap *= 2;
	}
	free(tmp);
	tmp = NULL;
}