非系统且不严谨的总结

一、数据清洗

数据清洗部分主要包括：缺失值处理、重复值处理、异常值处理。前两者简单，要么直接删掉，要么按照我们心仪的规则进行插值填充。而对于异常值，也可以直接删掉，但是并不是最好的做法。

如何检测异常值：

• 基于数据分布，当总体有先验的分布时，可以确定一个允许的概率，概率密度小于该值的观测视为异常值
• 基于分位数（四分位），一般取上限为比 Q3 大 1.5*(Q3-Q1) 的位置，下限同理

在以下情况下，可以直接删除异常值：

• 可以确定是有测量错误引起的，例如：2020年13月14日
• 异常值的占比非常小，具体多小看实际需要

反之则建议保留异常值，一般在检测异常值时已经确定上限和下限，可以通过盖帽法将数值限制在合理范围。具体如何处理还需要考虑用到的算法和建模需要。

二、特征转换

简单来说就是原始数据中可能存在非数值的特征，需要转换为数值型的特征。

对于分类数据（一般为文本形式），使用编码的方式将其赋值而转化为数值数据。如果本来存在先后顺序（如：高、中、低），则可以根据其含义赋值。如果是无顺序的分类（如：男、女），用的最多的是 One-Hot 编码，及其衍生的形式。更多的编码方式可以参考这篇文章。

对于数值数据，也可能需要进行进一步的编码（数值转为分类），即进行离散化。常见的方式有等宽分箱、等频分箱，或者通过无监督聚类来进行离散化。另外还可以将连续型数据二值化转化为离散数据（常用于计算机视觉中的特征转换）。

三、特征缩放

所谓特征缩放，就是当数据存在多个特征时，将各个特征的数值以某种规则限制在一个接近的范围。例如，特征中存在一个百分比数据（0-1），一个年龄数据（0-100）。在一些算法中（一般指使用欧氏距离衡量误差的算法），这种尺度的差异会影响各个特征的权重，导致结果受度量尺度的影响（但是从实际意义来看这个尺度不应该产生影响），因此需要进行特征缩放。常见方法有：

• 绝对最大值缩放：所有数据同时除以最大值；这样做的效果是，压缩到 [-1, 1] 的范围
• 最小最大缩放（归一化）：最小值作为 0，最大值作为 1，然后等比例压缩到 [0, 1] 之间；相比上一个方法，好处是不会出现负值
• Standardization（标准化）：所有数据同时减去均值再除以标准差
• Normalization（好像也叫标准化？？）：所有数据同时减去最小值再除以极差
• Regularization（正则化）：准确来说不属于特征缩放方法，而是在损失函数中加入惩罚项，作用类似放一起说了

如何选取特征缩放方法：

• 归一化：对数据结果范围有要求时使用；不存在极大或极小的离群值（否则大部分数据都挤在很小的范围内了）时使用
• 标准化：不适用归一化时使用
• 正则化：有 L1-Norm 和 L2-Norm 两种形式；前者得到 Lasso 模型，适用于需要筛选特征时（无关特征权重会置零）；后者得到 Ridge 模型，不会置零

关于上述方法的数学表示，这篇文章总结得很清晰，这里就懒得 latex 了。

三、特征选择

特征选择与后面提到的特征提取，同属于降维方法，关于降维技术的完整总结（含代码）参考这篇文章（备用链接），其关系大致如下：

• 降维
  • 特征选择
    • 相关性、前向选择、后向消除
  • 特征提取
    • 主成分分析、线性判别分析

数据存在多个特征，选择其中一个子集进行建模，称作特征选择。之所以要筛除部分特征，是因为维度过高的数据训练模型时容易产生过拟合，需要减小数据的维度以提高模型泛化能力。另一方面，也提高模型解释性和减少训练的难度。主要有以下方法：

• 过滤式选择：根据特征的信息量对特征进行排序，并筛除信息量较低的特征。衡量信息量一般有两类方法，一种是以特征和目标变量的相关性衡量（如皮尔逊相关系数），另一种是以特征的发散性衡量（如方差）。

• 包裹式选择：需要先确定一个算法模型，然后在不同特征子集上进行训练评估，最后选取最佳的子集。对于子集的分割，最直白的方式就是遍历所有组合。但是这样算法复杂度过高，因此衍生出不同的优化搜索算法。这个方法存在的问题是，需要事先确定一个学习算法，但是我们一开始不可能知道最优的算法。并且，不同算法得到的最优子集也是不同的。

• 嵌入式选择：Lasso 即为一个典型例子，将特征选择的功能“嵌入”在损失函数的惩罚项中。

四、特征提取

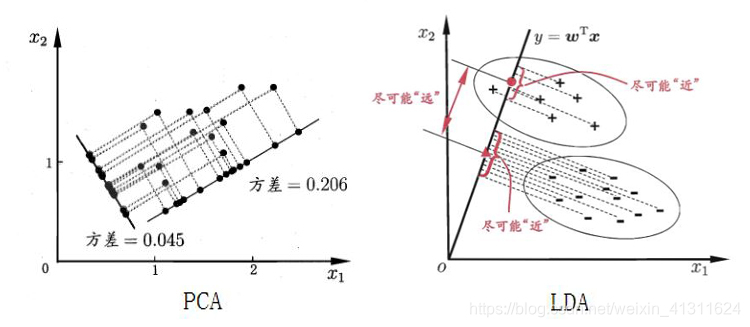
主成分分析（PCA）

简单来说，主成分分析执行的操作就是将特征进行一系列线性运算，将其映射到一个新的空间，用新的特征表示。具体怎么执行运算呢？其目标就是使新的特征相互正交，每个新的特征负责解释一个维度，并且使投影到新的空间时样本点的方差最大化（最大可分性）。原理很好理解，数学推导有点复杂，没捋清…

使用 PCA 可以将高维空间的特征投影到低维空间，丢弃了权重较小的主成分（往往是与目标变量的解释无关的信息，即噪声），使样本的采样密度增大，可以有效避免过拟合的问题。

核主成分分析（KPCA）是 PCA 的一个衍生方法，当特征从高维空间映射到低维空间不存在线性函数时，则需要进行核化，即非线性降维。下图很直观地解释了为什么需要非线性降维（来自“西瓜书”）：

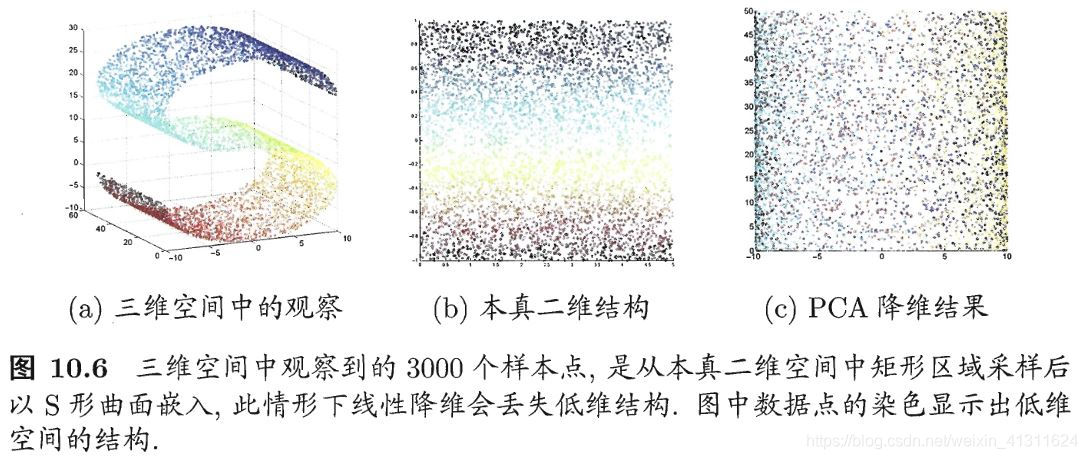
进行 PCA 时的注意事项：

• 什么时候适合使用 PCA：变量之间存在相关性、样本量足够大、数据无显著的异常值
• 由于协方差矩阵（PCA 算法的大致过程为：中心化、计算协方差矩阵、确定特征向量、通过特征向量投影特征空间）对变量的尺度敏感，所以进行 PCA 前需要进行数据缩放，即标准化
• 生成的主成分的性质：所有主成分均为原始特征的线性组合，所有主成分相互正交，按照解释的变异量排序
• PCA 的缺点：原始特征被组合在主成分之中，难以通过新的特征解释模型；并且有可能丢失重要的信息
• 评估 PCA 的效果：第一主成分权重越高越好

线性判别分析（LDA）

由于 PCA 是一种无监督学习方法，在将特征投影到新的空间时不考虑目标变量，有时候会导致在新特征上学习分类（分类问题中的特征多为不相关）变得更加困难，因此需要一种有监督的降维方法。LDA 有监督体现在，对特征进行投影时考虑了目标变量，它的目标是：使同类的尽可能靠近，不同类的点尽可能远离，最后将所有点投影到一条直线上。在进行分类时，同样将新样本投影到该直线，根据投影的位置来确定类别。在 PCA 中可以根据主成分解释的变异，选择任意需要的主成分数目，新特征的维度是任意的。在 LDA 中（分类问题），假设目标变量有 N 个类，则 LDA 产生的新特征的维度为 N-1。对于二分类问题，即投影到一条直线上。