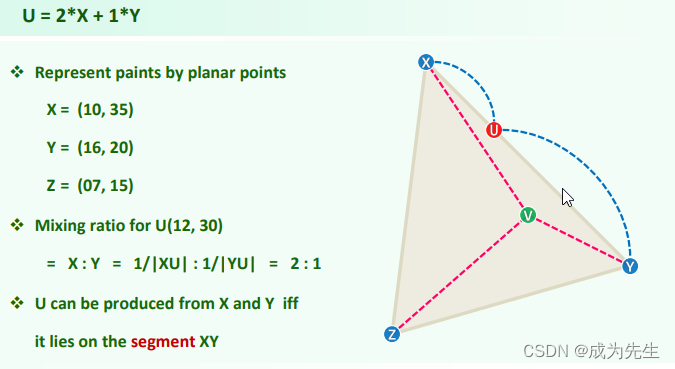
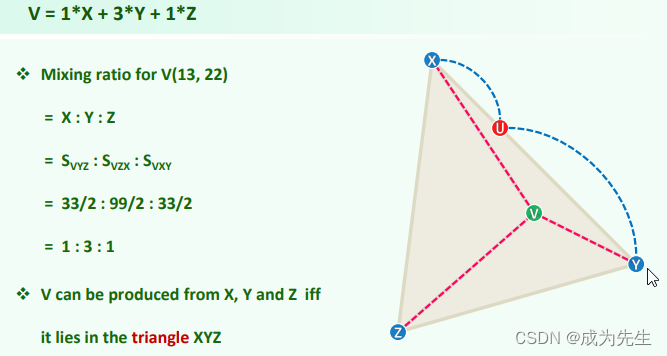
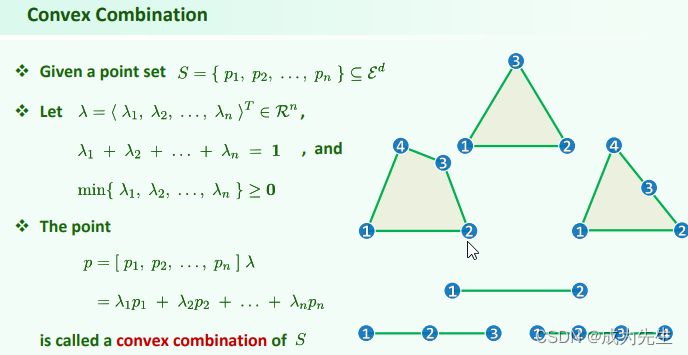
Covex combination和affine combination是两种常见的线性组合方法。

Covex combination（凸组合）是指在线性组合中，所有权重（coefficients）取非负值且总和为1的情况。也就是说，对于给定的一组向量或点集合，通过调整每个向量的权重，可以通过凸组合的方式得到该点集合内的任意一个点。凸组合在凸优化、图形学、计算几何等领域中经常被使用。

Affine combination（仿射组合）是指在线性组合中，所有权重取任意实数，并且总和为1的情况。与凸组合不同，仿射组合并不要求权重非负。在仿射组合中，不同权重的向量按照权重进行线性加权求和，得到一系列点的平均值或加权平均值。仿射组合在数学、计算机视觉、计算机图形学等领域中常常被使用。

总之，这两个概念都是表示向量或点集合的线性组合方式，其中covex combination要求权重非负并且总和为1，而affine combination则只要求总和为1。

当我们有两个向量 a 和 b 时，我们可以通过凸组合和仿射组合来生成新的向量。

例1：凸组合

假设向量 a = [1, 2]，向量 b = [3, 4]。通过凸组合，我们可以生成介于这两个向量之间的新向量。如果我们选择权重 w1 = 0.3 和 w2 = 0.7，则凸组合的结果可以计算如下：

凸组合 = w1 * a + w2 * b

= 0.3 * [1, 2] + 0.7 * [3, 4]

= [0.3, 0.6] + [2.1, 2.8]

= [2.4, 3.4]

因此，通过凸组合，我们得到了一个新向量 [2.4, 3.4]，它位于向量 a 和向量 b 之间。

例2：仿射组合

假设向量 a = [1, 2]，向量 b = [3, 4]。通过仿射组合，我们可以生成这两个向量的线性加权平均值。如果我们选择权重 w1 = 0.4 和 w2 = 0.6，则仿射组合的结果可以计算如下：

仿射组合 = w1 * a + w2 * b

= 0.4 * [1, 2] + 0.6 * [3, 4]

= [0.4, 0.8] + [1.8, 2.4]

= [2.2, 3.2]

因此，通过仿射组合，我们得到了一个新向量 [2.2, 3.2]，它是向量 a 和向量 b 的线性加权平均值。

以上两个例子分别展示了凸组合和仿射组合的应用，它们在处理向量和点集合时非常常见。注意，在实际问题中，可以有更多的向量和权重进行组合。这些例子只是为了说明概念。